| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞은 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 1 초 | 512 MB | 2198 | 853 | 592 | 37.516% |
문제
회전 초밥 음식점에는 회전하는 벨트 위에 여러 가지 종류의 초밥이 접시에 담겨 놓여 있고, 손님은 이 중에서 자기가 좋아하는 초밥을 골라서 먹는다. 초밥의 종류를 번호로 표현할 때, 다음 그림은 회전 초밥 음식점의 벨트 상태의 예를 보여주고 있다. 벨트 위에는 같은 종류의 초밥이 둘 이상 있을 수 있다.
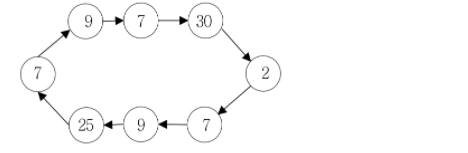
새로 문을 연 회전 초밥 음식점이 불경기로 영업이 어려워서, 다음과 같이 두 가지 행사를 통해서 매상을 올리고자 한다.
- 원래 회전 초밥은 손님이 마음대로 초밥을 고르고, 먹은 초밥만큼 식대를 계산하지만, 벨트의 임의의 한 위치부터 k개의 접시를 연속해서 먹을 경우 할인된 정액 가격으로 제공한다.
- 각 고객에게 초밥의 종류 하나가 쓰인 쿠폰을 발행하고, 1번 행사에 참가할 경우 이 쿠폰에 적혀진 종류의 초밥 하나를 추가로 무료로 제공한다. 만약 이 번호에 적혀진 초밥이 현재 벨트 위에 없을 경우, 요리사가 새로 만들어 손님에게 제공한다.
위 할인 행사에 참여하여 가능한 한 다양한 종류의 초밥을 먹으려고 한다. 위 그림의 예를 가지고 생각해보자. k=4이고, 30번 초밥을 쿠폰으로 받았다고 가정하자. 쿠폰을 고려하지 않으면 4가지 다른 초밥을 먹을 수 있는 경우는 (9, 7, 30, 2), (30, 2, 7, 9), (2, 7, 9, 25) 세 가지 경우가 있는데, 30번 초밥을 추가로 쿠폰으로 먹을 수 있으므로 (2, 7, 9, 25)를 고르면 5가지 종류의 초밥을 먹을 수 있다.
회전 초밥 음식점의 벨트 상태, 메뉴에 있는 초밥의 가짓수, 연속해서 먹는 접시의 개수, 쿠폰 번호가 주어졌을 때, 손님이 먹을 수 있는 초밥 가짓수의 최댓값을 구하는 프로그램을 작성하시오.
입력
첫 번째 줄에는 회전 초밥 벨트에 놓인 접시의 수 N, 초밥의 가짓수 d, 연속해서 먹는 접시의 수 k, 쿠폰 번호 c가 각각 하나의 빈 칸을 사이에 두고 주어진다. 단, 2 ≤ N ≤ 3,000,000, 2 ≤ d ≤ 3,000, 2 ≤ k ≤ 3,000 (k ≤ N), 1 ≤ c ≤ d이다. 두 번째 줄부터 N개의 줄에는 벨트의 한 위치부터 시작하여 회전 방향을 따라갈 때 초밥의 종류를 나타내는 1 이상 d 이하의 정수가 각 줄마다 하나씩 주어진다.
출력
주어진 회전 초밥 벨트에서 먹을 수 있는 초밥의 가짓수의 최댓값을 하나의 정수로 출력한다.
접근
끝 점이 없는 순환하는 투포인터 문제였다.
기본 N개의 테이블에 N + 1개부터 K개까지 데이터를 넣어 이어주면 간편하게 풀 수 있다.
초밥의 종류를 세는 것은 map을 쓰면 간단하다.
인덱스가 한칸 증가할 때마다 왼쪽 것을 없애주고, 오른쪽 것을 넣어주면 된다.
풀이
map인 cnt에 처음에 C 값과 1 ~ K 번째 초밥을 넣어주었다.
그 후 L을 N까지 증가시키면서 순회해주었다.
전위 후위 연산자를 너무 많이 사용하긴 했는데..
++R 번째 초밥을 cnt에 넣어주었고,
L번째 초밥을 빼주고 L을 증가시켜준 것이다.
이 때, cnt가 0이 되면 erase 시켜줘서 size를 줄여준다.
#include <bits/stdc++.h>
using namespace std;
#define ll long long int
#define FUP(i, a, b) for(int i = a; i <= b; i++)
#define FDOWN(i, a, b) for(int i = a; i >= b; i--)
#define MS(a, b) memset(a, b, sizeof(a))
#define ALL(v) v.begin(), v.end()
#define CIN(a) cin >> a;
#define CIN2(a, b) cin >> a >> b
#define CIN3(a, b, c) cin >> a >> b >> c
#define COUT(a) cout << a
#define COUT2(a, b) cout << a << ' ' << b
#define COUT3(a, b, c) cout << a << ' ' << b << ' ' << c
#define ENDL cout << '\n'
int dy[4] = { -1, 1, 0, 0 };
int dx[4] = { 0, 0, 1, -1 };
int N, D, K, C, ans = 0, arr[3003001];
map<int, int> cnt;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
CIN2(N, D);
CIN2(K, C);
FUP(i, 1, N) CIN(arr[i]);
FUP(i, N + 1, N + K) arr[i] = arr[i - N];
int L = 1, R = K;
cnt[C]++;
FUP(i, L, R) cnt[arr[i]]++;
ans = cnt.size();
while (L <= N)
{
cnt[arr[++R]]++;
if (--cnt[arr[L++]] == 0) cnt.erase(arr[L - 1]);
ans = max(ans, (int)cnt.size());
}
COUT(ans);
return 0;
}