| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞은 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 2 초 | 512 MB | 76 | 31 | 21 | 42.000% |
문제
취준생 태영이는 오랜 구직활동 끝에 취직에 성공했다. 여러가지 이유로 취업시장이 위축된 요즘, 가뭄의 단비 같은 일자리에 태영이는 기뻐했다. 하지만 모든 것은 계약되기 전에는 불확실한 법, 태영이는 하루빨리 근로계약서를 작성하고 싶은 마음에 밤잠을 설쳤다.
사회적 거리두기로 인한 언택트 시대, 태영이는 비대면 전자계약 서비스 모두싸인(MODUSIGN)을 이용해 근로계약서를 작성하게 되었다. 메일을 받은 후 태영이의 불안감은 사라졌고, 난생처음 작성해보는 계약서에 어떻게 하면 멋진 싸인을 할 수 있을지 행복한 고민을 시작했다.
태영이는 너무 튀지 않으면서도 독특한 느낌적인 느낌의 싸인을 만들고 싶다. 평소 기하학적인 감각이 돋보이던 태영이는 자신만의 룰을 지키며 싸인을 만드려고 한다. 태영이가 정한 룰은 다음과 같다.
- 태영이는 두 개의 볼록 다각형 A와 B를 정한다.
- 다각형 B는 완전히 A의 내부에 존재한다.
- 태영이의 싸인은 여러 개의 점을 차례로 이은 다각선이다.
- 태영이의 싸인을 구성하는 점은 A의 내부에 있어야 한다. 그리고 B의 외부에 있어야 한다.
- 도형의 외곽선 상에는 싸인의 점이 존재하지 않는다.
- 문제에서 주어지는 모든 좌표는 정수다.
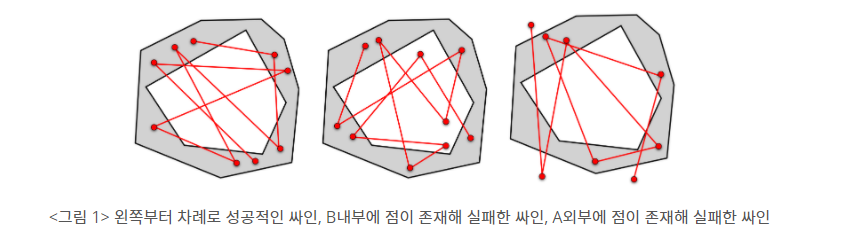
두 도형 A, B의 정보와 태영이가 싸인한 다각선의 정보가 입력으로 주어질 때, 해당 싸인은 주어진 규칙을 만족하는지 판단하는 프로그램을 작성해주자. 만약 태영이의 싸인이 규칙을 위반했다면, 몇 개의 점이 규칙을 위반했는지 계산하시오.
입력
첫 번째 줄에는 세 개의 자연수 N, M, K 가 공백으로 구분되어 주어진다.
- N 은 도형 A를 구성하는 점의 수이다. (3 ≤ N ≤ 10,000)
- M 은 도형 B를 구성하는 점의 수이다. (3 ≤ M ≤ 10,000)
- K 는 태영이의 싸인을 구성하는 점의 수이다. (2 ≤ K ≤ 300,000)
두 번째 줄에는 도형 A를 구성하는 N 개 점의 좌표가 공백으로 구분된 2N개의 정수로 주어진다. 각 점의 좌표는 X Y 형식으로 공백으로 구분되어 주어진다. 각 점은 반시계 방향 순서로 주어진다.
세 번째 줄에는 도형 B를 구성하는 M 개 점의 좌표가 공백으로 구분된 2M개의 정수로 주어진다. 각 점의 좌표는 X Y 형식으로 공백으로 구분되어 주어진다. 각 점은 반시계 방향 순서로 주어진다.
- 다각형 B의 모든 점은 다각형 A의 외곽선을 제외한 내부에 존재한다.
네 번째 줄에는 싸인을 구성하는 K개 점의 좌표가 공백으로 구분된 2K개의 정수로 주어진다. 각 점의 좌표는 X Y 형식으로 공백으로 구분되어 주어진다. 각 점을 차례로 이으면 태영이의 싸인이 완성된다.
- 모든 좌표는 정수 값을 가진다. (-1,000,000,000 ≤ X, Y ≤ 1,000,000,000)
- 문제에서 주어지는 점이 중복되는 경우는 존재하지 않는다.
- 싸인의 점은 도형 A, B의 외곽선상에 존재하지 않는다.
출력
주어진 싸인이 태영이의 규칙을 만족한다면 "YES" 를 출력하시오.
만약 태영이의 규칙을 만족하지 않는다면, 조건을 위반한 점의 개수를 정수로 출력하시오.
접근
이번 2020 SHAKE!에서 F번으로 나온 문제다.
문제를 본 순간 Convex hull 내부 점 판정 문제임을 알 수 있다.
하지만, K가 30만이라 한 점당 처리를 log의 속도로 해야된다.
이런 알고리즘은 접해본 적이 없어서 검색을 해봤는데, 잘 나오지 않았다.
찾아보던중 스택 오버플로우에서 탄젠트 값을 이분탐색으로 찾으면 된다는 글을 보았다.
좋은 풀이라고 생각해서 바로 코드로 옮겨보았다.
반시계방향으로 도형 A, B가 들어오므로 Convex Hull을 수행할 필요는 없었다.
다만, 탄젠트 값을 이분탐색으로 쓰기 위해서는 첫 인덱스의 X 좌표가 제일 왼쪽에 있는 좌표여야한다. (직접 그려보면 이해된다.)
그리고 첫 인덱스와 찾은 인덱스, 찾은 인덱스 + 1 삼각형과 점이 내부인지 외부인지 각각 판단해주면 문제가 해결된다.
A, B 비슷한 연산이 많아 복붙하다보니 오타가 많이나서 1시간을 날려먹었다.
풀이
코드가 좀 길어 주석으로 구분해놓았다.
플로우만 설명해보면, 대충 이렇다.
- 데이터 전처리(첫 인덱스를 가장 왼쪽 점으로 설정)
- 각 점마다 첫 인덱스를 기준으로 탄젠트값 설정
- A의 내부에 있는지 판별 (주석 참고)
- B의 외부에 있는지 판별 (3과 동일)
#include <bits/stdc++.h>
using namespace std;
#define ll long long int
#define FUP(i, a, b) for(int i = a; i <= b; i++)
#define FDOWN(i, a, b) for(int i = a; i >= b; i--)
#define MS(a, b) memset(a, b, sizeof(a))
#define ALL(v) v.begin(), v.end()
#define CIN(a) cin >> a;
#define CIN2(a, b) cin >> a >> b
#define CIN3(a, b, c) cin >> a >> b >> c
#define COUT(a) cout << a
#define COUT2(a, b) cout << a << ' ' << b
#define COUT3(a, b, c) cout << a << ' ' << b << ' ' << c
#define ENDL cout << '\n'
int dy[4] = { -1, 1, 0, 0 };
int dx[4] = { 0, 0, 1, -1 };
ll N, M, K, ans = 0, x = INT_MAX, y = INT_MAX;
pair<ll, ll> Atmp[10000], Btmp[10000];
vector<pair<ll, ll>> A, B;
double Btan[10000], Atan[10000];
ll CCW(ll x1, ll y1, ll x2, ll y2, ll x3, ll y3)
{
ll temp = x1 * y2 + x2 * y3 + x3 * y1;
temp = temp - y1 * x2 - y2 * x3 - y3 * x1;
if (temp > 0) return 1; //반시계반향
else if (temp < 0) return -1; //시계방향
else return 0; //일직선
}
// 데이터 전처리. x가 가장 작은 값을(가장 왼쪽 점) 0번째 인덱스로 놓는다.
void preprocessing()
{
int idx = -1; // 시작할 index (가장 작은 x)
FUP(i, 0, N - 1)
{
CIN2(Atmp[i].first, Atmp[i].second);
if (x > Atmp[i].first)
{
idx = i;
y = Atmp[i].second;
x = Atmp[i].first;
}
}
FUP(i, idx, idx + N - 1)
{
A.push_back(Atmp[i % N]);
}
idx = -1;
x = y = INT_MAX;
FUP(i, 0, M - 1)
{
CIN2(Btmp[i].first, Btmp[i].second);
if (x > Btmp[i].first)
{
idx = i;
y = Btmp[i].second;
x = Btmp[i].first;
}
}
FUP(i, idx, idx + M - 1)
{
B.push_back(Btmp[i % M]);
}
// 각도를 구한다. y / x의 값임. x가 0이면 나누기가 안되므로 큰 값으로 넣어줌.
FUP(i, 1, N - 1)
{
if (A[i].first == A[0].first)
{
Atan[i] = A[i].second > A[0].second ? 1e9 + 7 : -(1e9 + 7);
}
else
{
Atan[i] = ((double)A[i].second - A[0].second) / ((double)A[i].first - A[0].first);
}
}
FUP(i, 1, M - 1)
{
if (B[i].first == B[0].first)
{
Btan[i] = B[i].second > B[0].second ? 1e9 + 7 : -(1e9 + 7);
}
else
{
Btan[i] = ((double)B[i].second - B[0].second) / ((double)B[i].first - B[0].first);
}
}
}
bool checkA()
{
if (x <= A[0].first) return false; // 첫 좌표보다 X가 작거나 같으면 외부임. (외곽선에 점이 없으므로)
double tan = ((double)y - A[0].second) / ((double)x - A[0].first); // 첫 좌표로부터 탄젠트 값 구해줌
if (Atan[1] > tan || Atan[N - 1] < tan) return false; // 범위를 벗어난 값이면 외부임.
int left = 1, right = N - 1, mid, idx = 1;
while (left <= right) // 이분탐색
{
mid = (left + right) / 2;
if (tan == Atan[mid])
{
// 점이 겹치지 않으므로, 좌표의 값이 더 작으면 내부이고 더 크면 외부임.
if (x < A[mid].first) return true;
else return false;
}
if (tan > Atan[mid])
{
left = mid + 1;
idx = mid;
}
else
{
right = mid - 1;
}
}
// 내부에 있다면 모두 반시계방향임.
if (CCW(x, y, A[0].first, A[0].second, A[idx].first, A[idx].second) != 1) return false;
else if (CCW(x, y, A[idx].first, A[idx].second, A[idx + 1].first, A[idx + 1].second) != 1) return false;
else if (CCW(x, y, A[idx + 1].first, A[idx + 1].second, A[0].first, A[0].second) != 1) return false;
return true;
}
bool checkB()
{
if (x <= B[0].first) return true;
double tan = ((double)y - B[0].second) / ((double)x - B[0].first);
if (Btan[1] > tan || Btan[M - 1] < tan) return true;
int left = 1, right = M - 1, mid, idx = 1;
while (left <= right)
{
mid = (left + right) / 2;
if (tan == Btan[mid])
{
if (x < B[mid].first) return false;
else return true;
}
if (tan > Btan[mid])
{
left = mid + 1;
idx = mid;
}
else
{
right = mid - 1;
}
}
if (CCW(x, y, B[0].first, B[0].second, B[idx].first, B[idx].second) != 1) return true;
else if (CCW(x, y, B[idx].first, B[idx].second, B[idx + 1].first, B[idx + 1].second) != 1) return true;
else if (CCW(x, y, B[idx + 1].first, B[idx + 1].second, B[0].first, B[0].second) != 1) return true;
return false;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
CIN3(N, M, K);
preprocessing();
while (K--)
{
CIN2(x, y);
if (!checkA())
ans++;
else if (!checkB())
ans++;
}
!ans ? COUT("YES") : COUT(ans);
return 0;
}