📒 Optimization
모델의 최적화를 위한 다양한 방법론들을 배웠다.
이런것들이 있다라고 설명하고 넘어가는 방식이라 직접 하나하나 찾아봐야 될 것 같다.
한번씩 들어본 개념들이라서 수식을 제외하면 이해하기가 어렵지 않았다.
📝 Generalization
- 학습이 반복되면 Training error는 일반적으로 줄어든다.
- 학습에 사용하지 않은 Test error에 대해서는 시간이 갈수록 커진다.
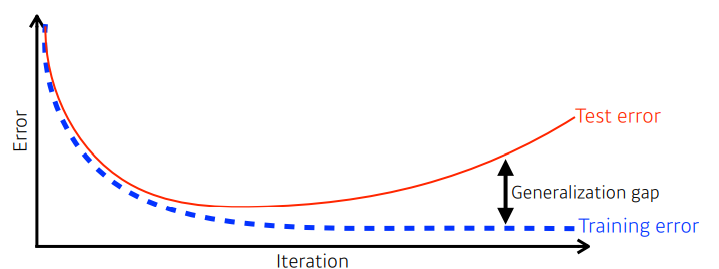
- 학습 data의 성능이 안좋으면, test data의 성능도 나빠진다.
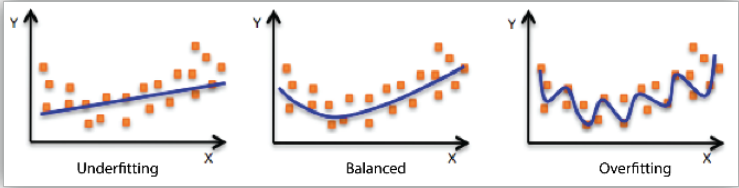
- 학습 data에는 적합하지만, traning에는 적합하지 않은 모델이 overfitting이다.
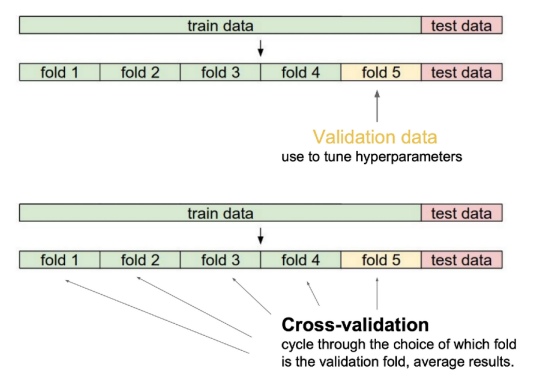
✏️ Cross-validation
- validation data : 학습시키지 않은 데이터
- 학습 데이터를 K개로 나눠서 K - 1개로 학습시키고, 나머지로 test를 하는 것이다.
✏️ Bias and Variance
- Variance : 데이터를 넣었을 때 출력이 얼마나 일관적으로 나오는가?
- Bias : target과 얼마나 벗어났는가?
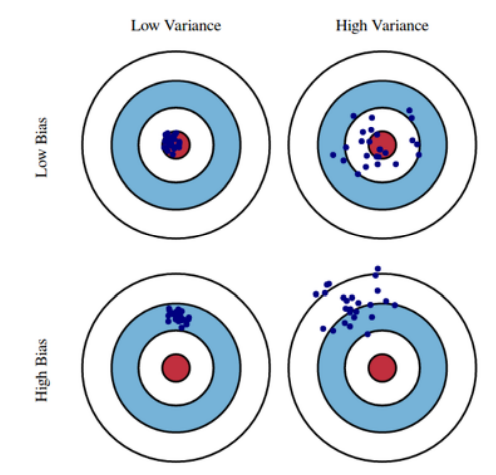
- 학습 데이터에 noise가 있는 경우 bias와 variance는 반비례할 확률이 크다.

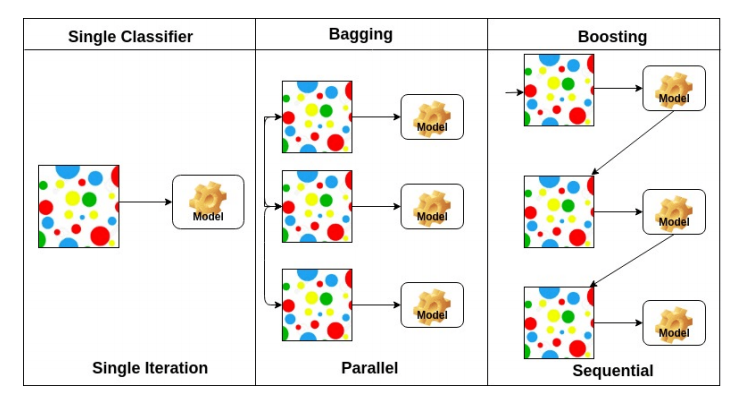
✏️ Bootstrapping
학습 데이터가 고정되어 있을때 subsampling을 통해 학습 데이터를 여러개로 만들고 그것을 가지고 여러 모델을 만들어서 무언가를 하는 방법
📝 Gradient Descent Methods
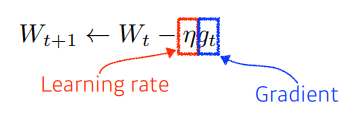
✏️ Gradient Descent
- Linear Network가 있을 때, loss functon에 대한 gradient를 구해서 parameter를 빼주는 방법
- 줄었을 때 optimal이라고 기대하는 loss function이 존재
- 찾고자하는 parameter에 대해 loss function의 편미분 값을 이용해 학습
- 극소적으로 작은 local minimum만 찾을 수 있다.
✏️ Kind of Gradient Descent
- Stochastic gradient descent
- 한번에 한개의 gradient를 구해서 update를 반복
- single sample을 통해서 gradient를 구한다.
- Mini-batch gradient descent
- Batch size의 sample을 통해서 gradient를 구하고 update
- 일반적으로 딥러닝에서 많이 사용하는 방법이다.
- Batch gradient descent
- 데이터를 한번에 다 써서 gradient를 update한다.
✏️ Gradient Descent Method
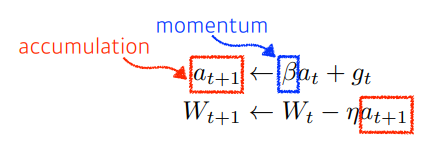
- Momentum : 이전 batch의 gradient 정보를 활용한다. (관성)
- Nesterov Accelerated Gradient : 한 번 이동한 후 계산
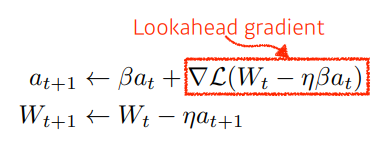
- Adagrad : 많이 변한 parameter를 적게 변화, 아닌 경우는 많이 변화
- 뒤로 갈수록 W가 커져 변화량이 적어짐
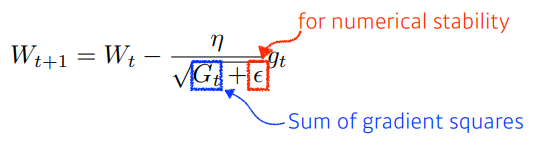
- 뒤로 갈수록 W가 커져 변화량이 적어짐
- Adadelta : Adagrad의 Gt가 커지는 현상을 막기 위한 방법
- Window size(시간)에 대한 gradient 제곱의 변화를 확인한다.
- learning rate가 없어 바꿀 수 있는 수단이 별로 없다.
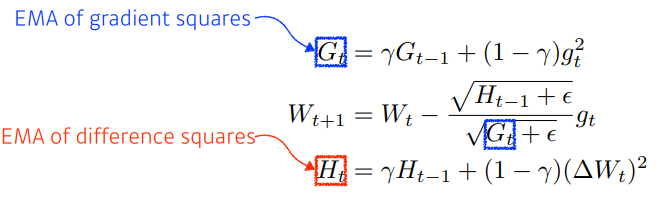
- RMSprop : gradient squares를 단순히 누적하지 않고, 최신 값들이 더 크게 반영
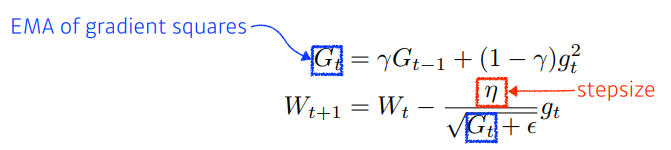
- Adam : gradient squares를 가져가면서, momentum도 활용한다.

📝 Regularization
학습을 방해하는게 목적으로, 학습 데이터에서만 잘 동작하는 것이 아니라 테스트 데이터에서도 잘 동작할 수 있게 만들어주는 기법
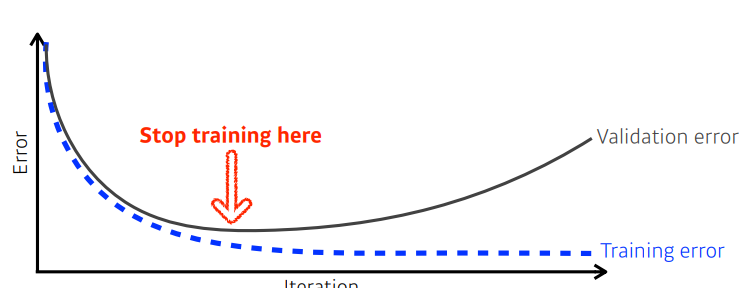
✏️ Early stopping
- validation error를 활용해서 loss가 커지기 시작할 때 멈추는 방법
✏️ Parameter Norm Penalty
- parameter가 너무 커지지 않게 하는 방법 (모두 줄인다.)
- 크기(abs)는 작으면 작을수록 좋기 때문이다.
- 부드러운 함수일 수록 Generalization 가능성이 높을 것이다.

✏️ Data Augmentation
- 주어진 데이터를 이용해 데이터를 최대한 늘리는 방법
- label이 바뀌지 않는 한도내에서 데이터를 조금씩 바꿔서 활용한다.
✏️ Noise Robustness
- 입력 데이터, weight에 noise를 넣으면 테스트 단계에서 더 잘 될수 있다?

✏️ Label Smoothing
- 분류 문제를 풀 때 데이터가 한정적이면 쓸만한 방법

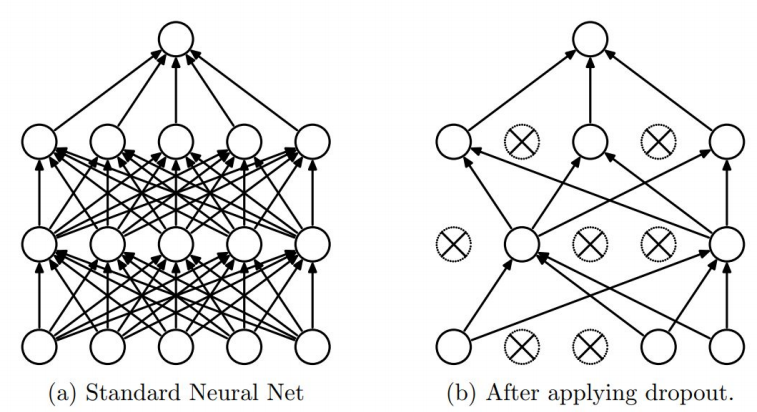
✏️ Dropout
- 학습을 진행하면서 각 Layer에 존재하는 노드들을 무작위로 On / Off를 반복한다.
- 무작위로 선택된 노드들의 weight만 사용해서 다음 layer에서 전파된다.
- Overfitting을 방지할 수 있는 효과를 얻는다.
✏️ Batch Normalization
- Layer 간의 Internal Covariate Shift 문제를 해결하기 위해 고안되었다.
- 각 Layer들마다 Normalization을 해서 변형된 분포가 나오지 않게 작업하는 것이다.
- minibatch들마다 정규화를 실시한다.

📒 CNN 첫걸음
교수님의 보폭이 너무 큰 것이 아닌가 하는 생각이 든다..
앞부분은 크게 어렵지 않았는데, 역전파 부분에서 굉장히 빠르게 지나갔다.
적당히 복습하면 이해할 수 있을 것 같긴 하다.
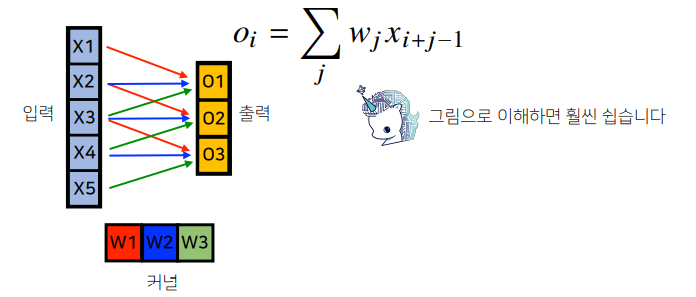
📝 Convolution
- 고정된 가중치인 커널(kernel)을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조
- 활성화 함수를 제외한 Convolution 연산도 선형변환에 속한다.
- i번째 위치에 따라 가중치 행렬이 따로 존재하지 않으므로 parameter size가 많이 줄어든다.
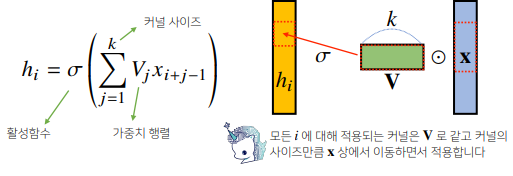
- signal을 커널을 이용해 국소적으로 증폭 또는 감소시켜서 정보를 추출하는 것이다.
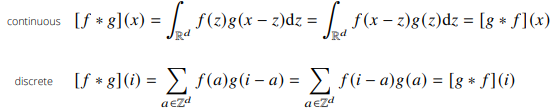
- 1차원뿐만 아니라 다양한 차원에서 계산 가능하다.
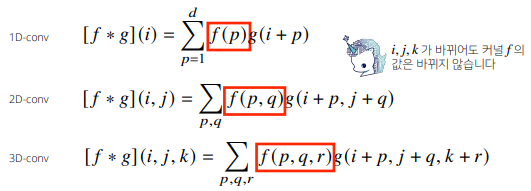
📝 2D Convolution
- 이미지 위에서 stride 값 만큼 filter를 이동
👉 겹쳐지는 부분의 각 원소의 값을 곱해서 모두 더한 값을 출력으로 하는 연산
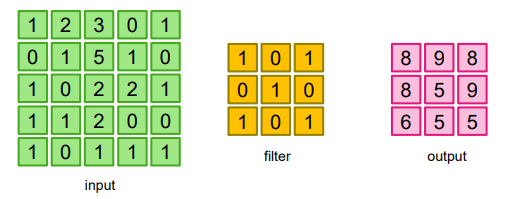
- 각 인덱스에서 두 행렬을 mul 한 뒤, sum 연산을 취한다고 생각하면 될 듯 하다.

- stride : filter를 한번에 얼마나 이동할 것인가
- padding : 0으로 이미지 상하좌우에 padding 값 만큼 감싼다.
- 입력 크기가 (H, W), 커널 크기가 (Kh, Kw), 출력 크기가 (Oh, Ow)일 때 식
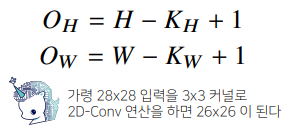
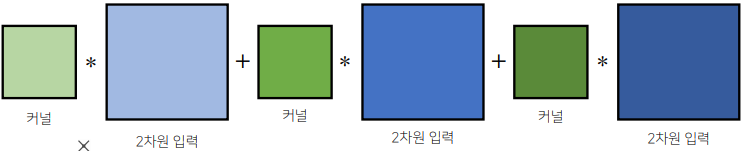
- 채널이 여러개인 2차원 입력(3차원)의 경우 2차원 Convolution을 채널 개수만큼 적용
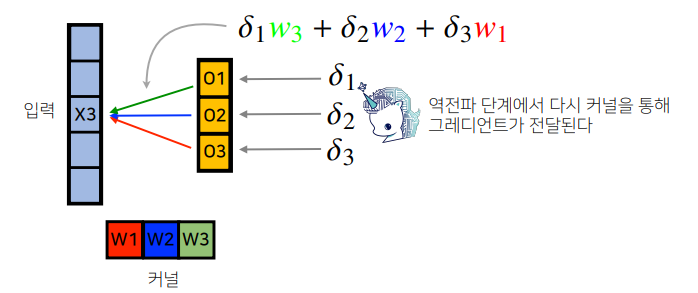
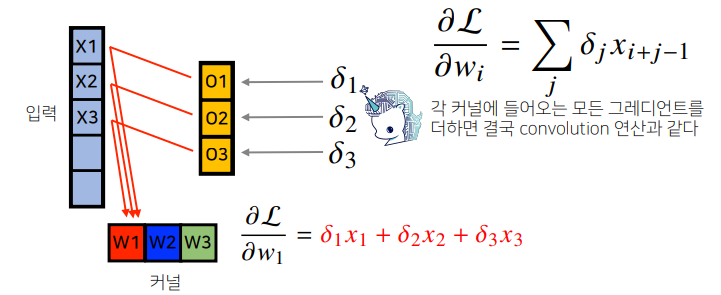
📝 역전파
- 역전파를 계산할 때도 convolution 연산이 나온다.


📒 [퀴즈] CNN 첫걸음- 1~5
5/5 Solve
📝 Q1
Q) 다음 보기 중, 연속적인 변수에 대한 함수 f, g 사이의 convolution을 나타내는 수식으로 가장 적절한 것을 고르시오.
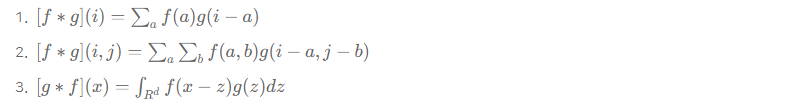
A) 3
📝 Q2
Q) 입력 벡터 x 와 가중치 벡터 V가 다음과 같이 주어질 때, 다음 보기 중 올바른 h를 고르시오.

✔️1. h = [-14, -20, -26, -32, -38, -44, -52, -60]
2. h = [-6, -12, -18, -24, -30, -36, -42, -48, -54, -60]
3. h = [-3, -8, -14, -20, -26, -32, -38, -44, -52, -60, -29, -10]
h[0] = -1 * 1 + -2 * 2 + -3 * 3 = -14📝 Q3
Q) 벡터 x와 h가 다음과 같이 주어질 때, y1 값을 구하시오.

A) 14
y1 = 1 * 4 + 2 * 5 = 14 (식에 오류가 있다.)📝 Q4
Q) 입력 행렬 X와 커널 K가 다음과 같이 주어질 때, Y(1,2) 값을 구하시오

A) 5
Y(1,2) = 0 * 1 + 1 * 2 + 1 * 3 + 0 * 4 = 5📝 Q5
Q) 입력 행렬 X와 커널 K가 다음과 같이 주어질 때, Y(2,2) + Y(3,3) 값을 구하시오

A) 9
Y(2,2) = 1 * 1 + 0 * 2 + 1 * 3 + 0 * 4 = 4
Y(3,3) = 0 * 1 + -1 * 2 + 1 * 3 + 1 * 4 = 5