[JS] 최소 힙 구현, 다익스트라 구현 - BOJ 1916 최소비용 구하기

김규리·2025년 3월 18일

JavaScript MinHeap dijkstra 다익스트라 자료구조 최소 힙

알고리즘

목록 보기

1/1

자바스크립트로 코딩테스트를 본다...? 몇몇 사람들은 띠용?이라고 생각한다. 왜냐면 javascript는 heap, queue 등의 자료구조를 직접 구현해야 하기 때문이다. ㄱ-

다익스트라 알고리즘의 경우, 최소 비용을 빠르게 찾기 위해 최소 힙을 사용한다. 하지만 개발자들을 강하게 키우는 자바스크립트는 우선순위 큐, heap같은 자료구조는 직접 구현해야 한다.

직접 최소 힙을 구현해보고, 다익스트라 알고리즘을 이용해 백준 1916번 문제를 풀어 보자.

최소 힙

우선순위 큐

우선순위 큐는, 우선순위가 가장 높은 데이터를 가장 먼저 삭제하는 자료구조이다.

우선순위 큐를 구현하려면 배열을 이용하거나 힙(Heap)을 이용해 구현할 수 있다. 각각 배열과 힙으로 우선순위 큐를 구현했을 때, 삽입 시간과 삭제 시간의 시간복잡도는 다음과 같다.

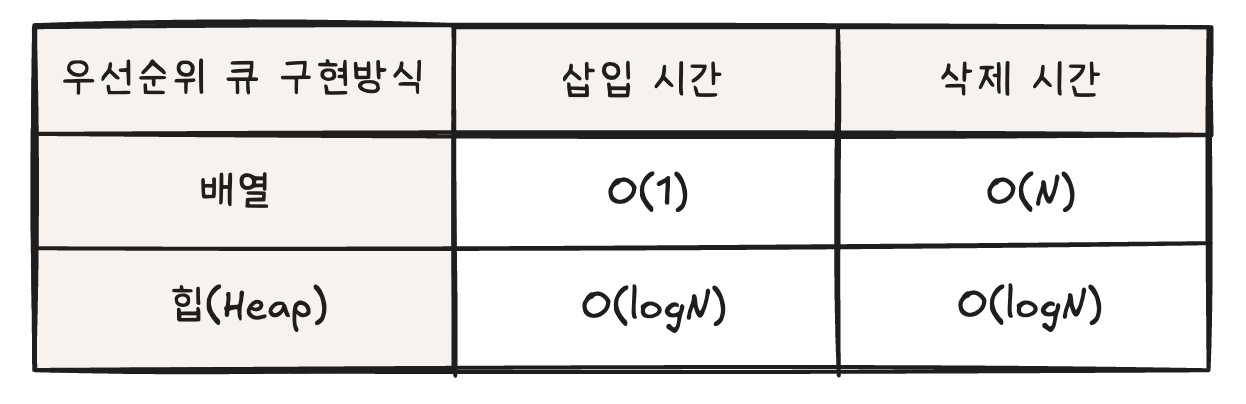
힙(Heap) 자료구조 구현

힙은 완전 이진 트리 자료구조의 일종이다.

🎄 완전 이진 트리란?
완전 이진 트리란 루트 노드부터 시작하여 왼쪽 자식 노드, 오른쪽 자식 노드 순서대로 데이터가 차례대로 삽입되는 트리를 의미한다.

힙은 항상 루트 노드를 제거한다.

그러면 우선순위 큐는 우선순위가 가장 높은 데이터를 가장 먼저 삭제한다 했으니, 가장 우선순위가 높은 데이터를 루트 노드에 저장하면 된다! 이러한 힙의 특성 때문에 우선순위 큐를 효율적으로 구현할 수 있으며, 힙은 다익스트라 알고리즘과 같은 그래프 알고리즘에서 유용하게 사용된다.

우선 순위를 가장 작은 값으로 할지, 가장 큰 값으로 할 지에 따라 최소 힙과 최대 힙으로 나뉜다.

최소 힙

최소 힙(min heap)은 루트 노드가 가장 작은 값을 가진다. 따라서 값이 작은 데이터가 우선적으로 제거된다.

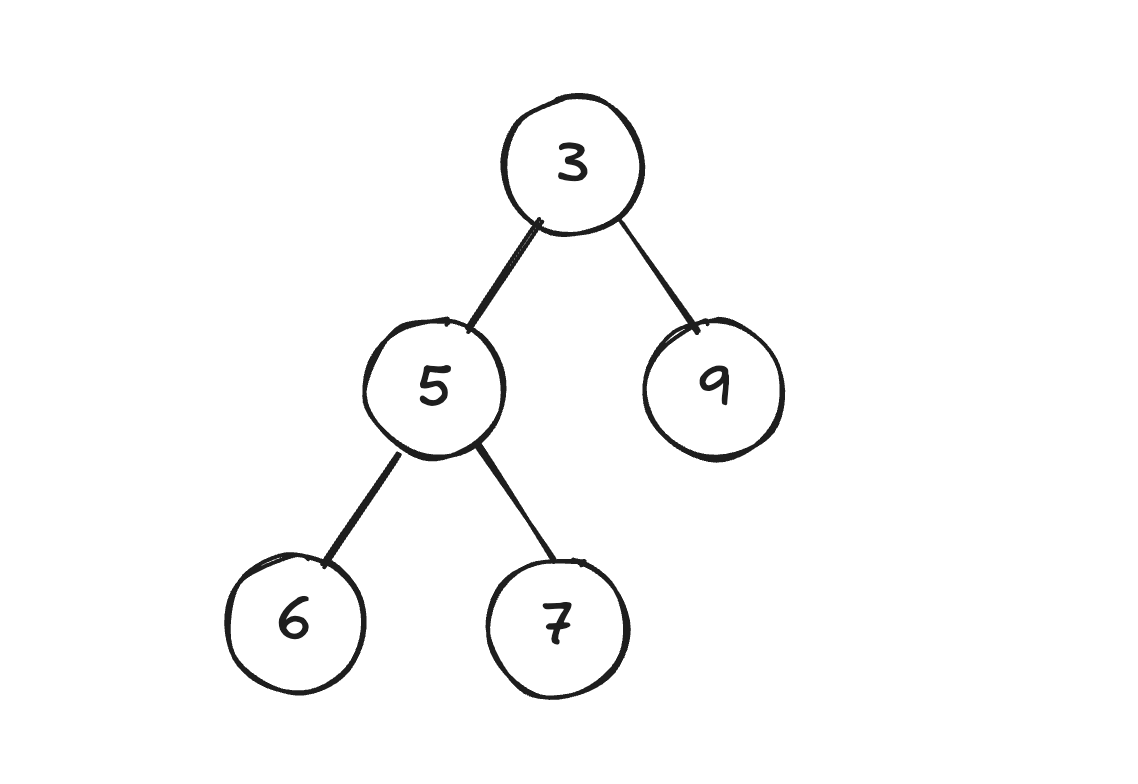
최소 힙의 예시이다. 가장 작은 값인 3이 루트 노드에 있다.

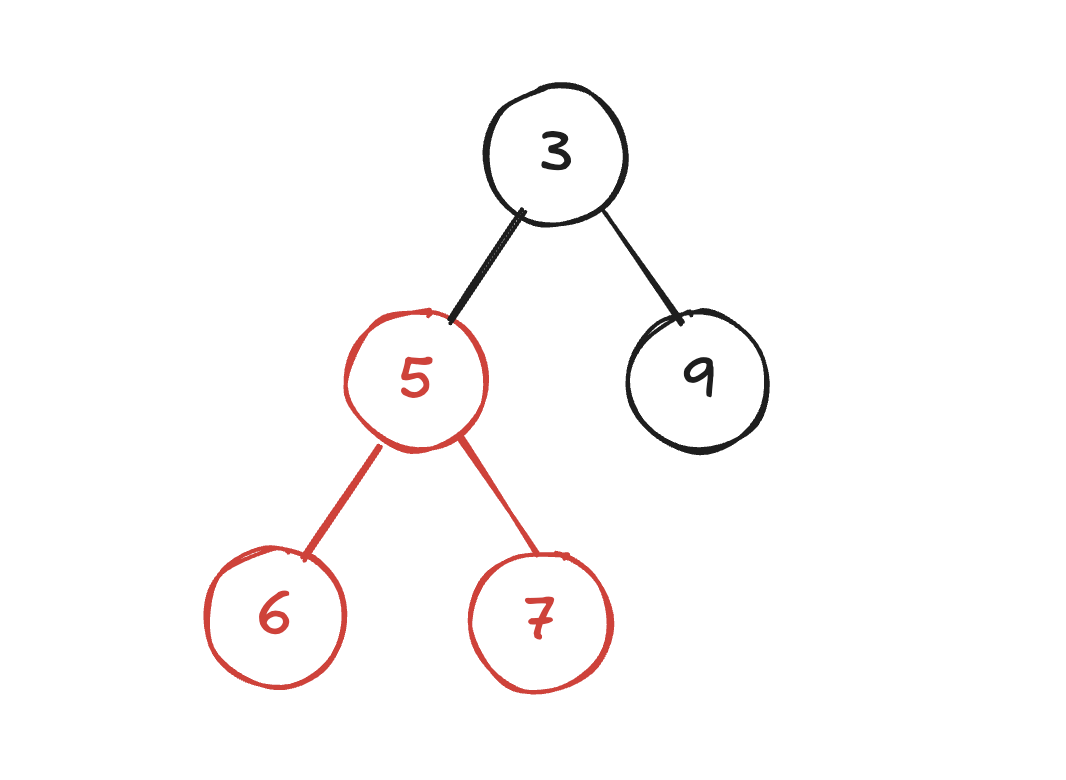
또한, 서브트리를 보면 가장 작은 5가 서브트리의 루트 노드인 것을 확인할 수 있다. 즉, 최소 힙에서 부모 노드는 자식보다 작은 값을 가져야 한다.

반대로 최대 힙(max heap)은 루트 노드가 가장 큰 값을 가진다. 따라서 값이 큰 데이터가 우선적으로 제거된다.

heapify()

최소 힙을 구현하려면, 다음과 같은 조건을 만족해야 한다.

루트 노드에는 가장 작은 값이 들어갈 것.
데이터는 왼쪽 노드부터 오른쪽 노드 순으로 삽입되어 완전 이진 트리 조건을 만족할 것.

데이터 삽입이나 삭제가 일어나더라도 위의 조건을 만족하려면 계속해서 정렬을 해줘야 한다. 이 때, heap 자료구조를 재정렬하는 것을 heapify() 라고 한다.

데이터를 삽입할 때의 heapify를 알아보자.

데이터 삽입 - 상향식 재정렬, heapifyUp()

데이터를 삽입할 땐, 우선 가장 끝에 데이터를 넣는다. 이렇게 하면 완전 이진 트리 조건을 만족한다.

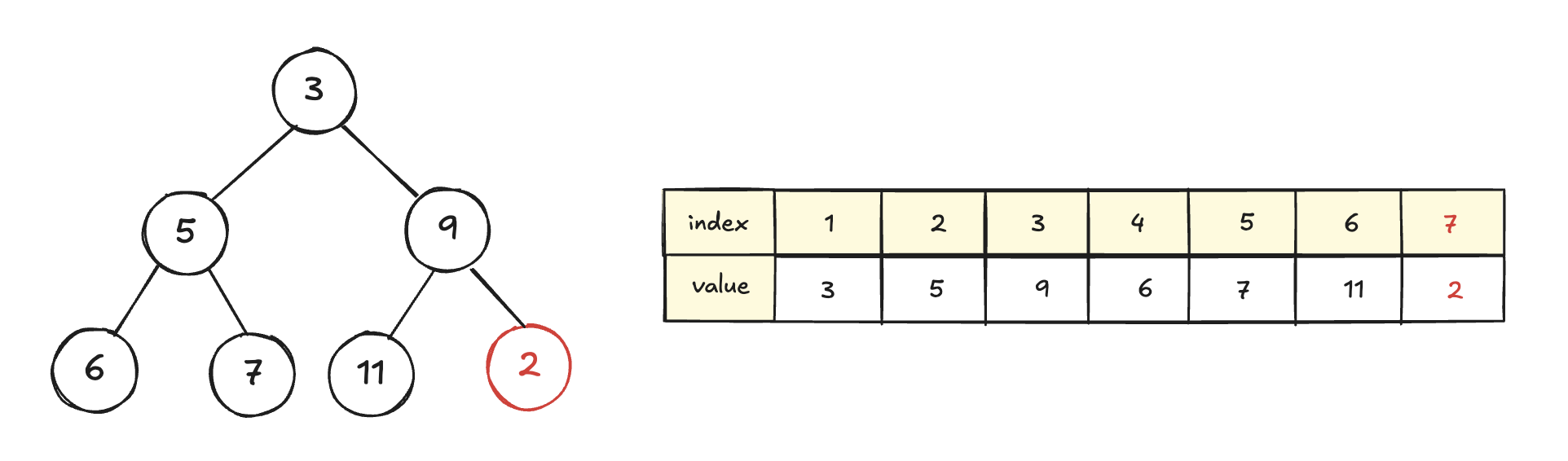
하지만 이렇게 트리의 맨 끝에 넣으면, 루트 노드가 가장 작아야 한다는 min heap의 조건을 위배하게 된다!

따라서 부모와 자신을 비교하여 부모가 더 크면 swap한다.

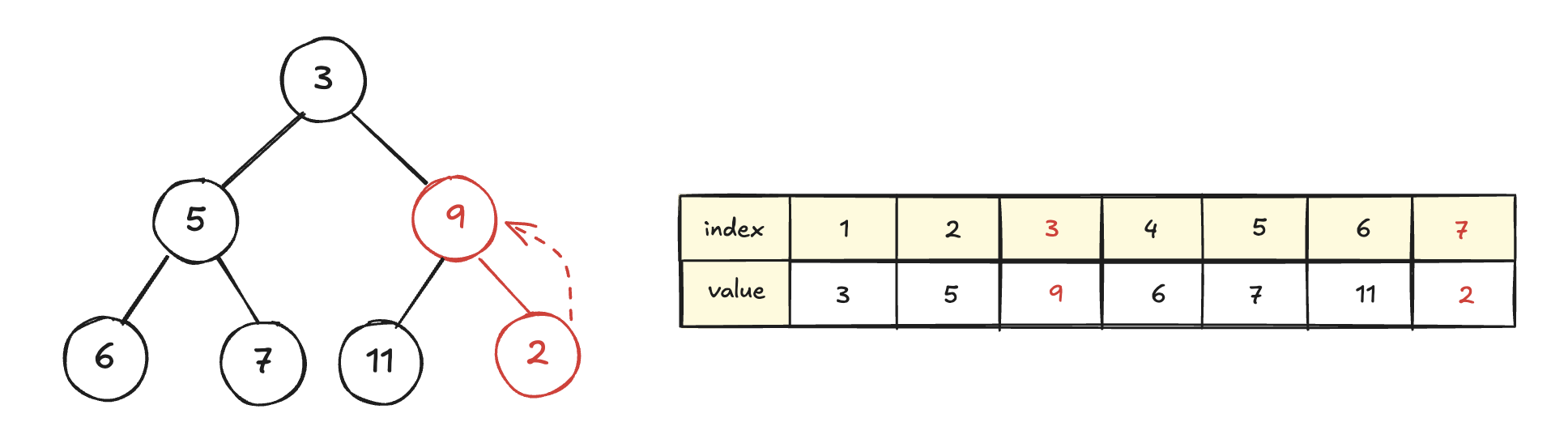
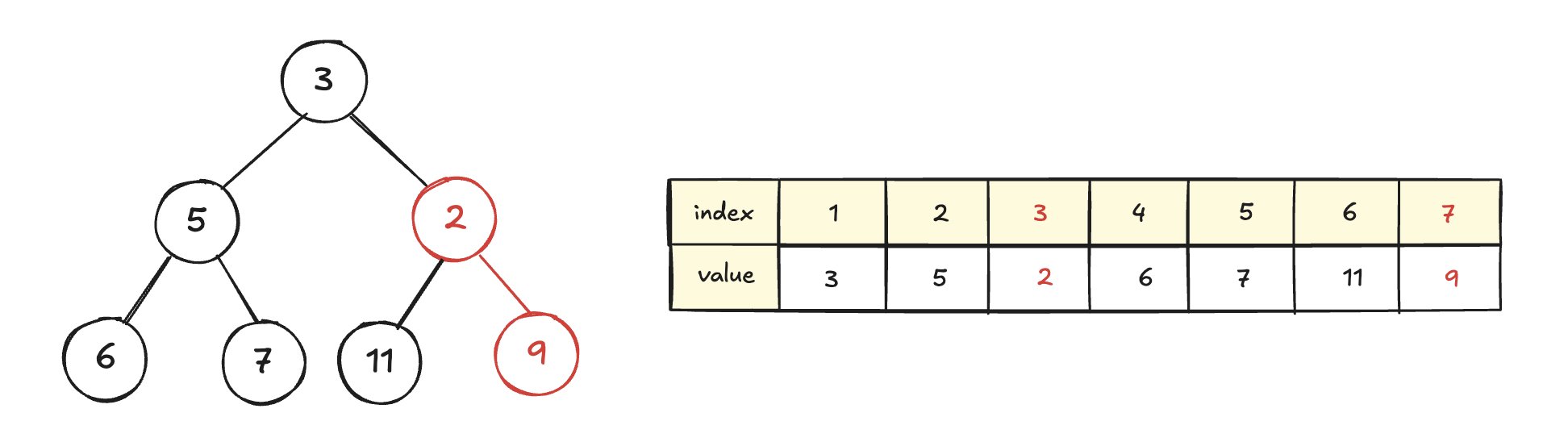
다시 부모와 자신 중 부모가 더 크다면 swap한다.

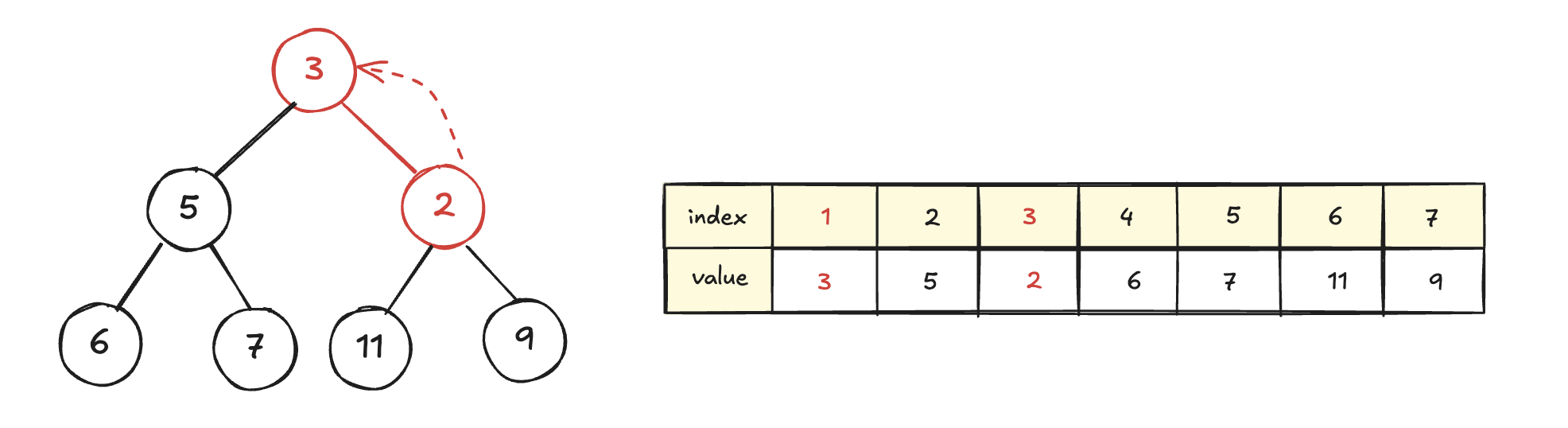
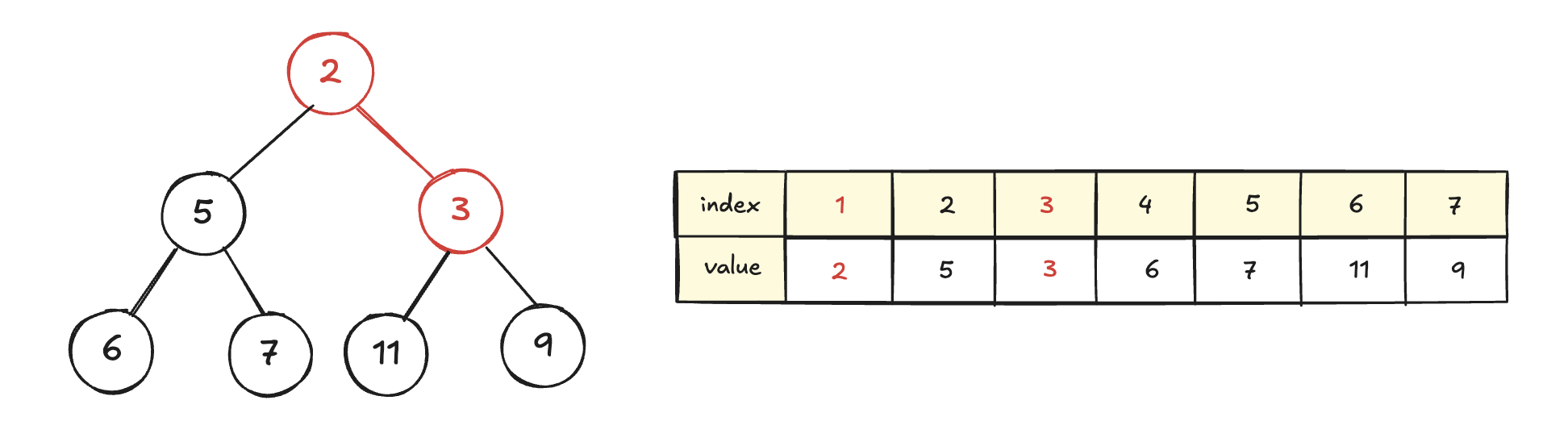
이 과정을 더 이상 swap이 일어나지 않거나, 자기 자신의 인덱스가 0이 될 때까지 반복한다.

heapifyUp을 javascript 코드로 구현하면 다음과 같다.

class MinHeap {
	constructor() {
    	this.heap = [-1];
	}
  
  	insert(node) {
    	this.heap.push(node);
      	this.heapifyUp();
    }
  
	...
    
    heapifyUp() {
        // 완전 이진 트리를 유지하기 위해 가장 끝에 들어왔음
    	let index = this.heap.length - 1;
      
      	// 더 이상 swap이 일어나지 않거나, 부모 index가 0이 될 때까지 반복
    	while (index > 0) {
        	let parentIndex = this.getParentIndex(index);
            if (this.heap[index] < this.heap[parentIndex]) {
            	this.swap(index, parentIndex);
              	index = parentIndex;
            } else {
            	break;
            }
        }
    }
}

데이터 삭제 - 하향식 재정렬, heapifyDown

Heap 자료구조는 pop할 때, 루트 노드를 리턴한다. 즉 heap[1] 을 리턴한다.

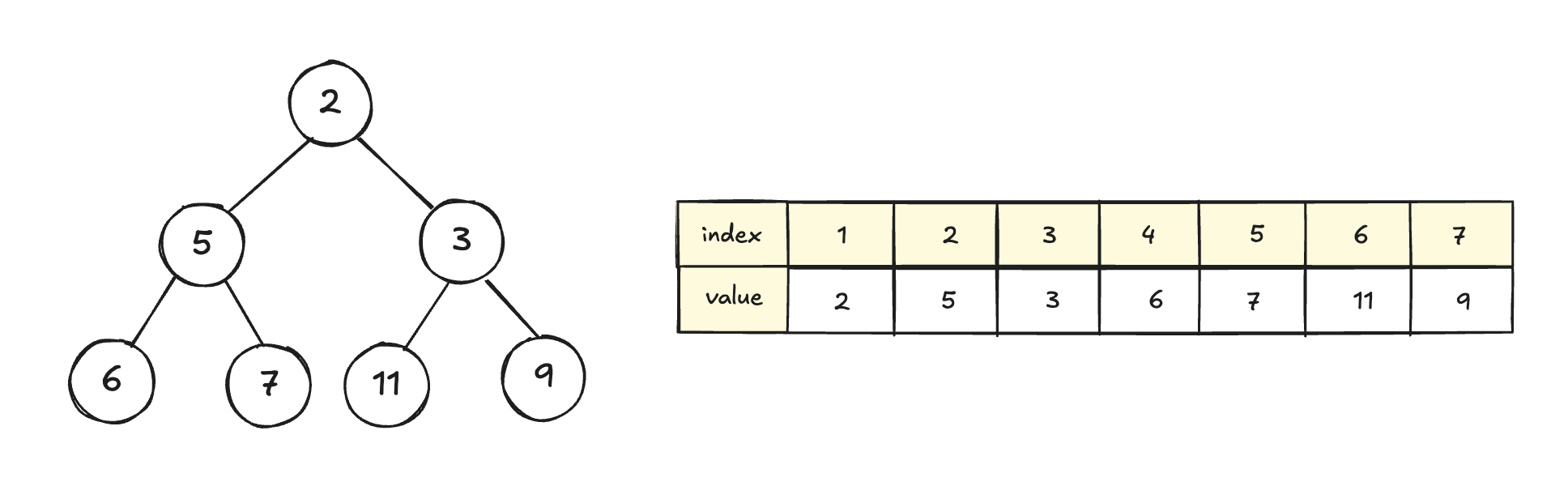
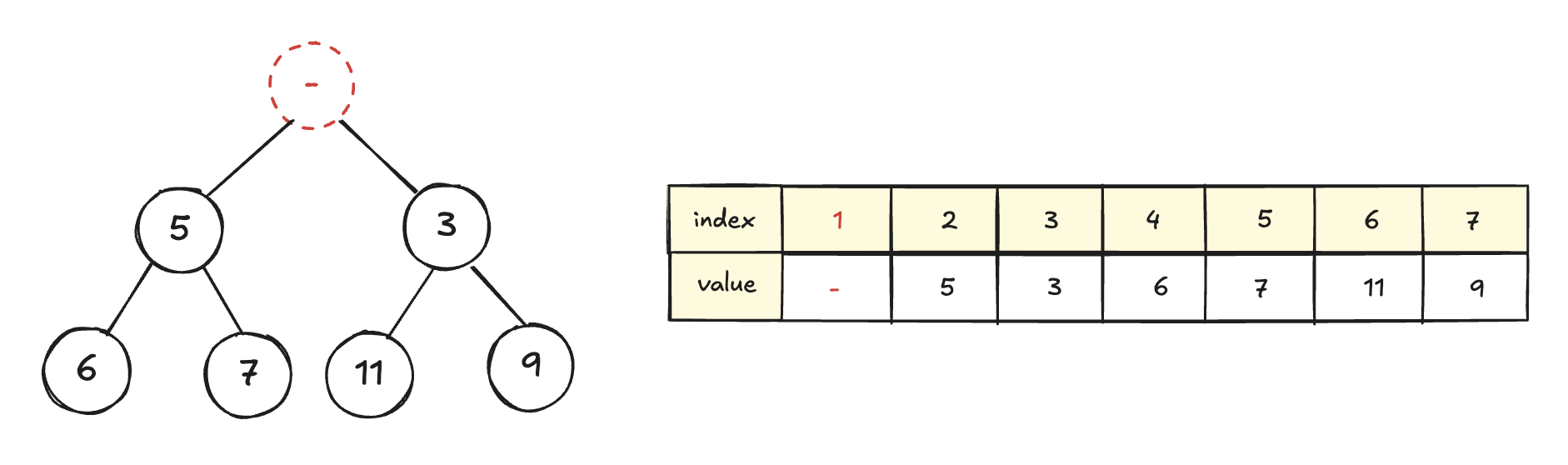
하지만 루트 노드가 사라지고 나면 완전 이진 트리의 구조가 깨지고, 루트 노드에 최소값이 들어가야 한다는 min heap의 조건도 지켜지지 않는다. 비어있는 루트 노드에 어떻게 다음으로 가장 작은 값을 넣을까?

우선 가장 마지막 노드를 '일단' root에 넣어둔다.
그러면 완전 이진 트리의 형태를 유지하게 된다.

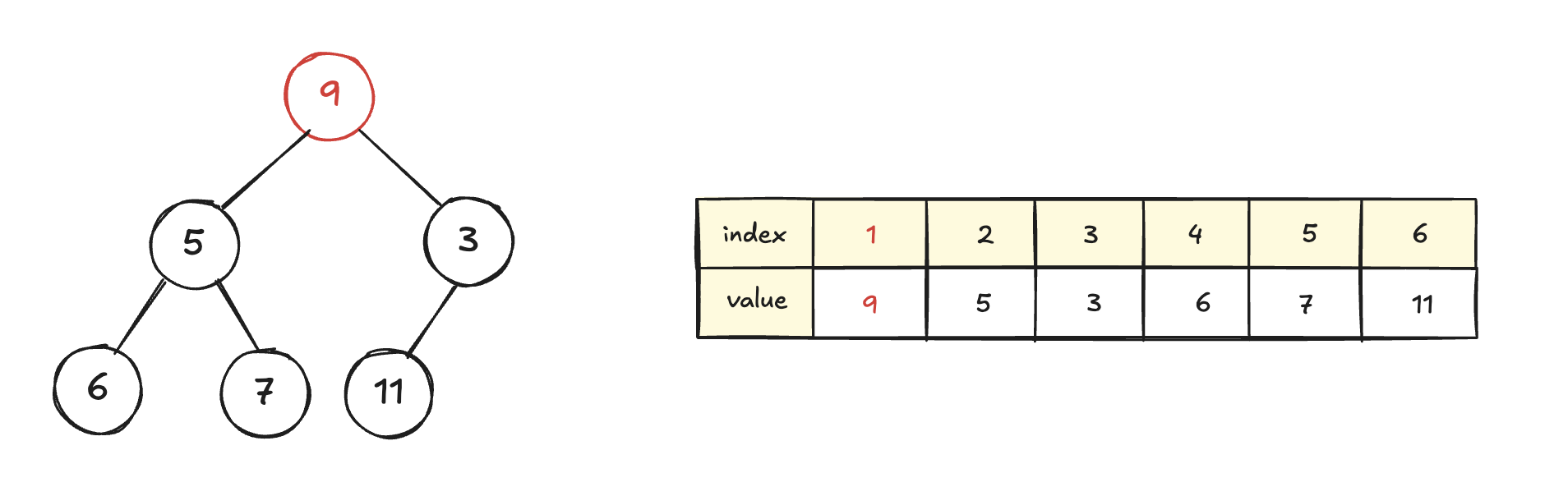
하지만 이 상태는 최소 힙의 조건인 "루트 노드에 최소값을 저장한다"는 조건을 위배한다.

이 문제를 해결하기 위해, 왼쪽, 오른쪽 자식들과 자신을 비교해서 나보다 작은 자식이 존재한다면, 가장 작은 자식과 나를 swap하면 된다.

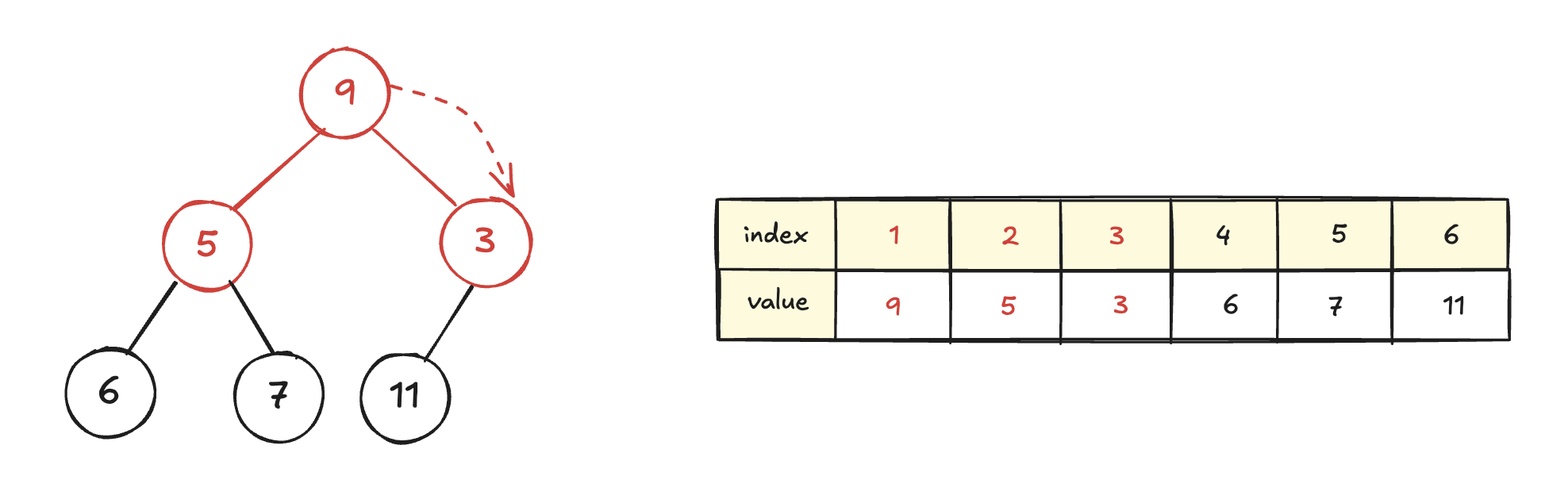
9, 5, 3 중 가장 작은 값은 오른쪽 자식인 3이므로, 3과 9를 swap한다. 이 과정을 더 이상 swap하지 못하거나 트리의 끝까지 도달할 때까지 반복하면 된다.

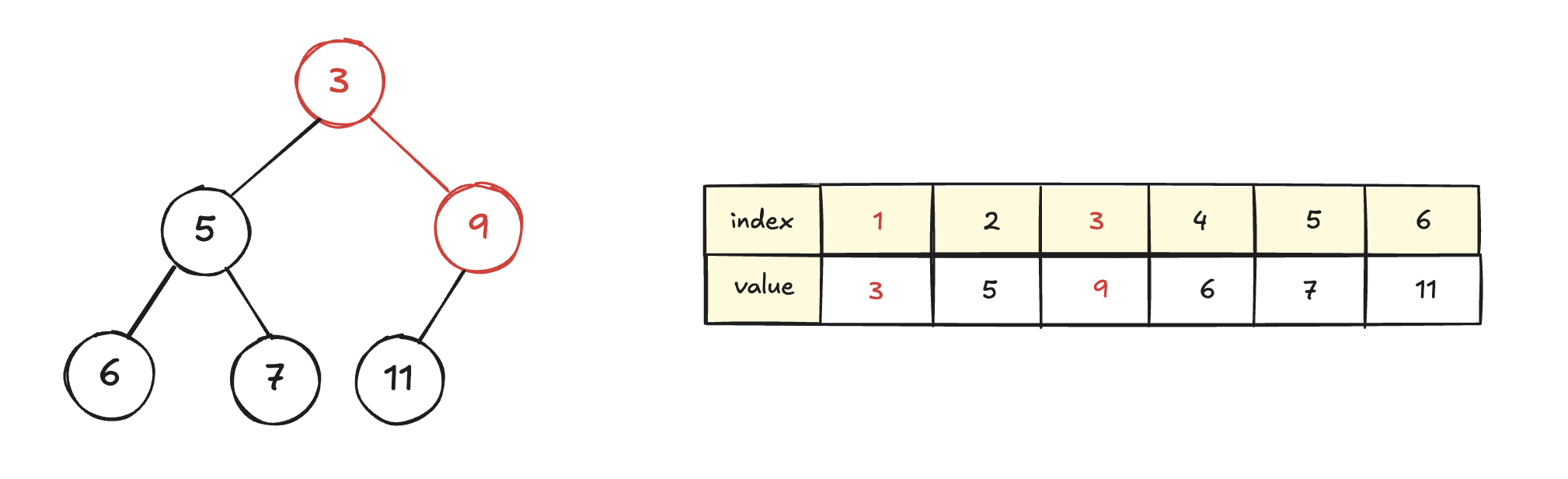
다음 9 기준 자식 노드들은 부모 노드보다 크므로 더 이상 swap이 발생하지 않게 되고, heapifyDown 함수를 멈추면 된다.

코드는 다음과 같다.

class MinHeap {
	constructor() {
    	this.heap = [-1];
	}
  
  	pop() {
      	// 아무것도 들어있지 않은 경우
      	if (this.heap.length === 1) return null;
      
    	const minNode = this.heap[1];
      	const last = this.heap.pop();
      	// minNode !== last 인 경우 재정렬
      	if (this.heap.length > 1) {
        	this.heap[1] = last;
          	this.heapifyDown();
        }
      
      	return minNode;
    }
  
	...
    
    heapifyDown() {
        // 완전 이진 트리를 유지하기 위해 가장 끝에 들어왔음
    	let index = 1
        const length = this.heap.length;
      
      	// 더 이상 swap이 일어나지 않거나, 트리 끝까지 가기 전까지 반복
    	while (true) {
          	const leftChildIndex = this.getLeftChildIndex(index);
          	const rightChildIndex = this.getRightChildIndex(index);
          
          	// 가장 작은 value를 가진 index를 저장할거임
          	let smallest = index;
          
        	// 왼쪽 자식 노드가 존재하면서, 왼쪽 자식 노드의 값이 더 작으면 swap
          	if (leftChildIndex < length && this.heap[leftChildIndex] < this.heap[smallest]) {
            	smallest = leftChildIndex;
            }
          
          	// 오른쪽 자식 노드가 존재하면서, 오른쪽 자식 노드의 값이 더 작으면 swap
          	if (rightChildIndex < length && this.heap[rightChildIndex] < this.heap[smallest]) {
            	smallest = rightChildIndex;
            }
          
          	// 현재 노드가 가장 작은 노드가 아니면 위치 교환
            if (smallest !== index) {
                this.swap(index, smallest);
                index = smallest;
            } else {
              	break;
            }
        }
    }
}

MinHeap 구현

javascript에서 min heap을 구현하는 전체 코드는 다음과 같다...
~~.... 길다 길어!~~

class MinHeap {
  constructor() {
    // index 1을 root node로 접근하기 위해..
    this.heap = [-1];
  }

  getParentIndex(index) {
    return Math.floor(index / 2);
  }

  getLeftChildIndex(index) {
    return 2 * index;
  }

  getRightChildIndex(index) {
    return 2 * index + 1;
  }

  swap(index1, index2) {
    [this.heap[index1], this.heap[index2]] = [this.heap[index2], this.heap[index1]];
  }

  insert(node) {
    this.heap.push(node);
    this.heapifyUp();
  }

  pop() {
    if (this.heap.length === 1) return null;

    const minNode = this.heap[1];
    const last = this.heap.pop();

    if (this.heap.length > 1) {
      this.heap[1] = last;
      this.heapifyDown();
    }

    return minNode;
  }

  heapifyUp() {
    let index = this.heap.length - 1;

    while (index > 0) {
      const parentIndex = this.getParentIndex(index);
      if (this.heap[parentIndex] > this.heap[index]) {
        this.swap(parentIndex, index);
        index = parentIndex;
      } else {
        break;
      }
    }
  }

  heapifyDown() {
    let index = 1;
    const length = this.heap.length;

    while (true) {
      const leftChildIndex = this.getLeftChildIndex(index);
      const rightChildIndex = this.getRightChildIndex(index);
      let smallest = index;

      if (leftChildIndex < length && this.heap[leftChildIndex] < this.heap[smallest]) {
        smallest = leftChildIndex;
      }

      if (rightChildIndex < length && this.heap[rightChildIndex] < this.heap[smallest]) {
        smallest = rightChildIndex;
      }

      if (smallest !== index) {
        this.swap(index, smallest);
        index = smallest;
      } else {
        break;
      }
    }
  }

  isEmpty() {
    return this.heap.length === 1;
  }
}

이래서 다들 javascript로 코테 준비하다가 다른 언어로 도망가나보다 ㅎㅎ..
하지만 나는 해낸다..! 아자아자

다익스트라

다익스트라 알고리즘은, 한 정점에서 모든 정점까지의 최단 거리를 각각 구하는 알고리즘이다. 문제에서 한 정점에서 다른 정점으로 가는 최단 거리(최소 비용)를 물어봤다면, 다익스트라 알고리즘을 사용하는 것이 효율적이다.

다익스트라 알고리즘과 비슷한 플로이드-워셜 알고리즘은, 모든 노드 쌍들에 대한 최단 거리를 구하는 알고리즘이다.

다익스트라 구현 방법

"너 시작점에서 v의 이웃인 w에 갈건데, v를 거쳐 갈래 그냥 갈래?"

다익스트라 알고리즘은 그래프에서 한 정점에서 다른 모든 정점까지의 최단 경로를 찾는 알고리즘이다. 최소 힙을 활용하면 이 과정을 효율적으로 구현할 수 있다.

초기화
- 출발점으로부터의 최단 거리를 저장할 배열 d[v]를 생성
- 출발 노드의 거리는 0으로, 나머지 모든 노드는 무한대(Infinity)로 설정
- 시작 노드와 그 거리(0)를 최소 힙에 삽입
최단 거리 노드 선택
- 최소 힙에서 현재 가장 거리가 짧은 노드를 추출
  - 이때 최소 힙은 '거리'를 기준으로 정렬되어 있음
- 추출된 노드를 v, 해당 노드까지의 거리를 dist라고 정의
인접 노드 거리 갱신
- v와 연결된 모든 인접 노드 w에 대해
  - 새로운 경로 거리 = d[v] + w.dist
  - 기존 경로 거리 = d[w]
  - 만약 새로운 경로 거리가 기존 경로 거리보다 짧다면
    - d[w]를 새로운 값으로 갱신
    - (노드, 갱신된 거리) 쌍을 최소 힙에 삽입
반복
- 최소 힙이 비거나 목적지 노드가 처리될 때까지 2~3단계를 반복
종료 조건
- 목적지 노드가 처리되면 해당 노드까지의 최단 거리를 반환
- 또는 최소 힙이 비어 더 이상 처리할 노드가 없으면 목적지에 도달할 수 없음

최소 힙을 사용함으로써 항상 현재 알려진 최단 경로를 가진 노드를 효율적으로 선택할 수 있다.

이 때, 2번을 보면 가장 가까운 노드를 선택하는 과정이 있는데, 위에서 공부한 최소 힙을 사용해 가장 가까운 노드를 사용한다. 덕분에 빠르게 현재 알려진 최단 경로를 가진 노드를 효율적으로 선택할 수 있다.

그렇다면 실제로 백준 1916번에 적용하여 문제를 풀어보자.

실전 - 백준 1916. 최소비용 구하기

백준 1916번 바로가기

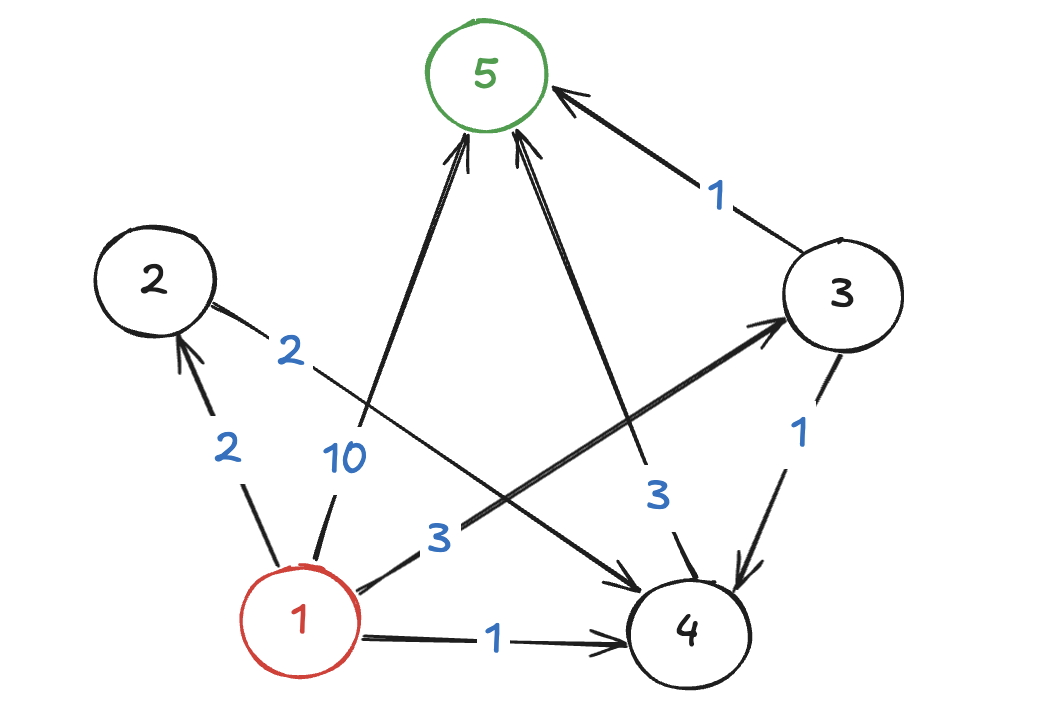
해당 그래프는 백준 1916번 문제의 예제 1이다.
정점 1에서 정점 5로 가는 최단거리를 알아보자.

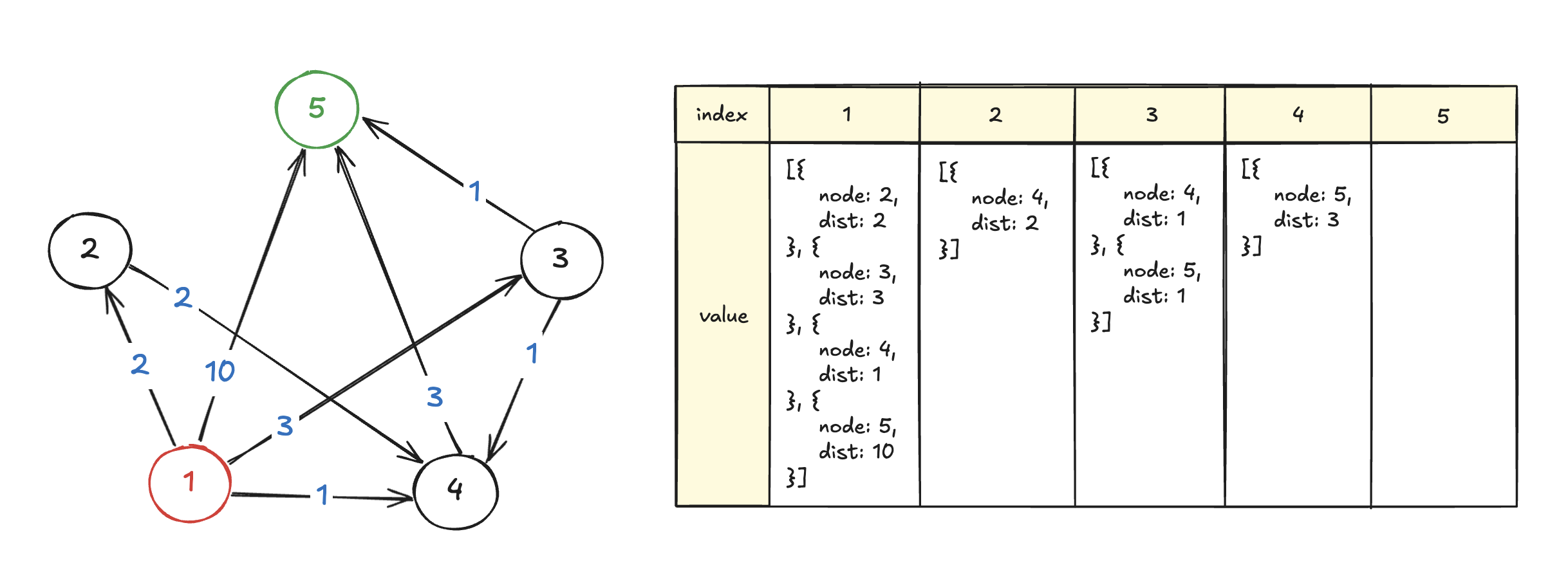
이런식으로 정점과 간선의 관계를 저장했다.

const graph = Array.from({ length: N + 1 }, () => []);
for (let i = 2; i < M + 2; i++) {
  const [v, w, dist] = inputs[i].split(" ").map(Number);
  graph[v].push({ node: w, dist });
}

시작점은 1이므로, 시작점을 1로 두고 다익스트라 알고리즘을 실행해보자.

초기화

출발점으로부터의 최단 거리를 저장할 배열 d[v]를 생성

출발 노드의 거리는 0으로, 나머지 모든 노드는 무한대(Infinity)로 설정

시작 노드와 그 거리(0)를 최소 힙에 삽입

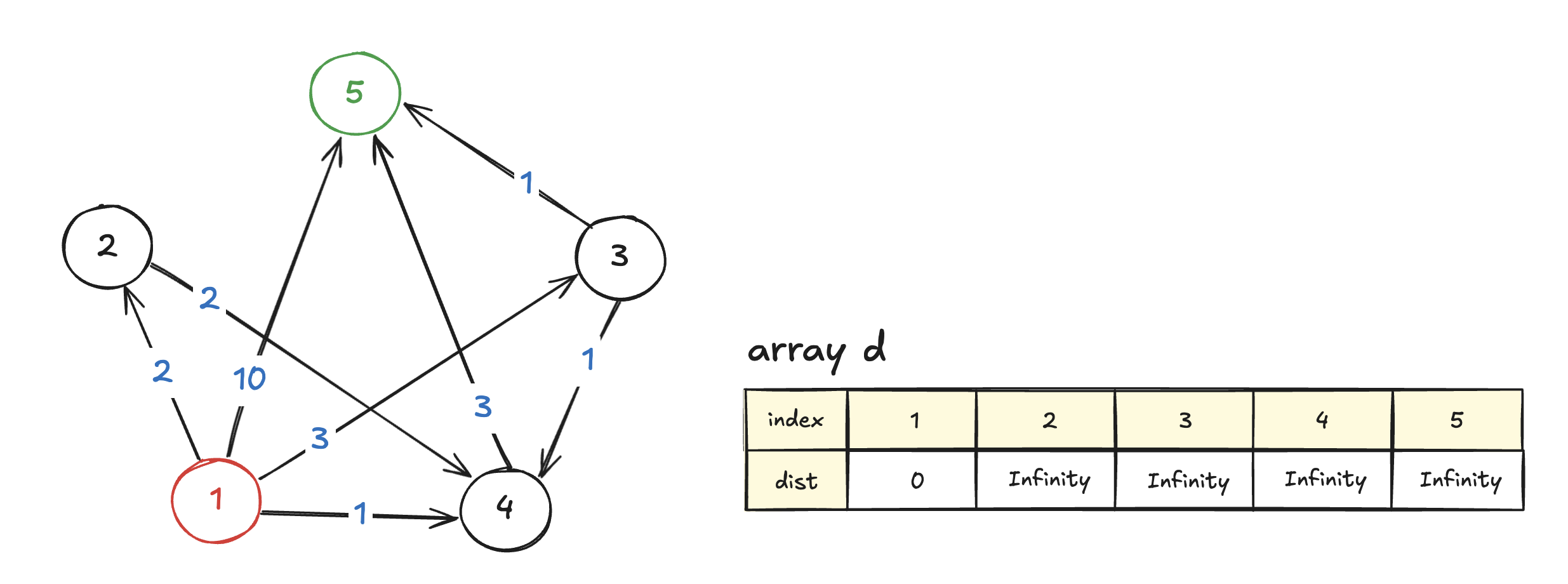
const d = new Array(N + 1).fill(Infinity);
d[start] = 0;

const minHeap = new MinHeap();
minHeap.insert({ node: start, dist: 0 });

최단 거리 노드 선택

최소 힙에서 현재 가장 거리가 짧은 노드를 추출

이때 최소 힙은 '거리'를 기준으로 정렬되어 있음

추출된 노드를 v, 해당 노드까지의 거리를 dist라고 정의

while (!minHeap.isEmpty()) {
  	const { node: v, dist } = minHeap.pop();

    // 현재 거리가 이미 알려진 최소 거리보다 크면 무시
    if (dist > d[v]) continue;
  
  	// 도착지면 끝
    if (v === end) return dist;
  	...
}

인접 노드 거리 갱신

v와 연결된 모든 인접 노드 w에 대해

새로운 경로 거리 = d[v] + w.dist

기존 경로 거리 = d[w]

만약 새로운 경로 거리가 기존 경로 거리보다 짧다면

d[w]를 새로운 값으로 갱신

(노드, 갱신된 거리) 쌍을 최소 힙에 삽입

반복

최소 힙이 비거나 목적지 노드가 처리될 때까지 2~3단계를 반복

while (!minHeap.isEmpty()) {
  	...
    // 이웃 노드들 확인
    if (graph[v]) {
      for (const { node: w, dist: distW } of graph[v]) {
        const newDist = dist + distW;

        if (newDist < d[w]) {
          d[w] = newDist;
          minHeap.insert({ node: w, dist: newDist });
        }
      }
    }
}

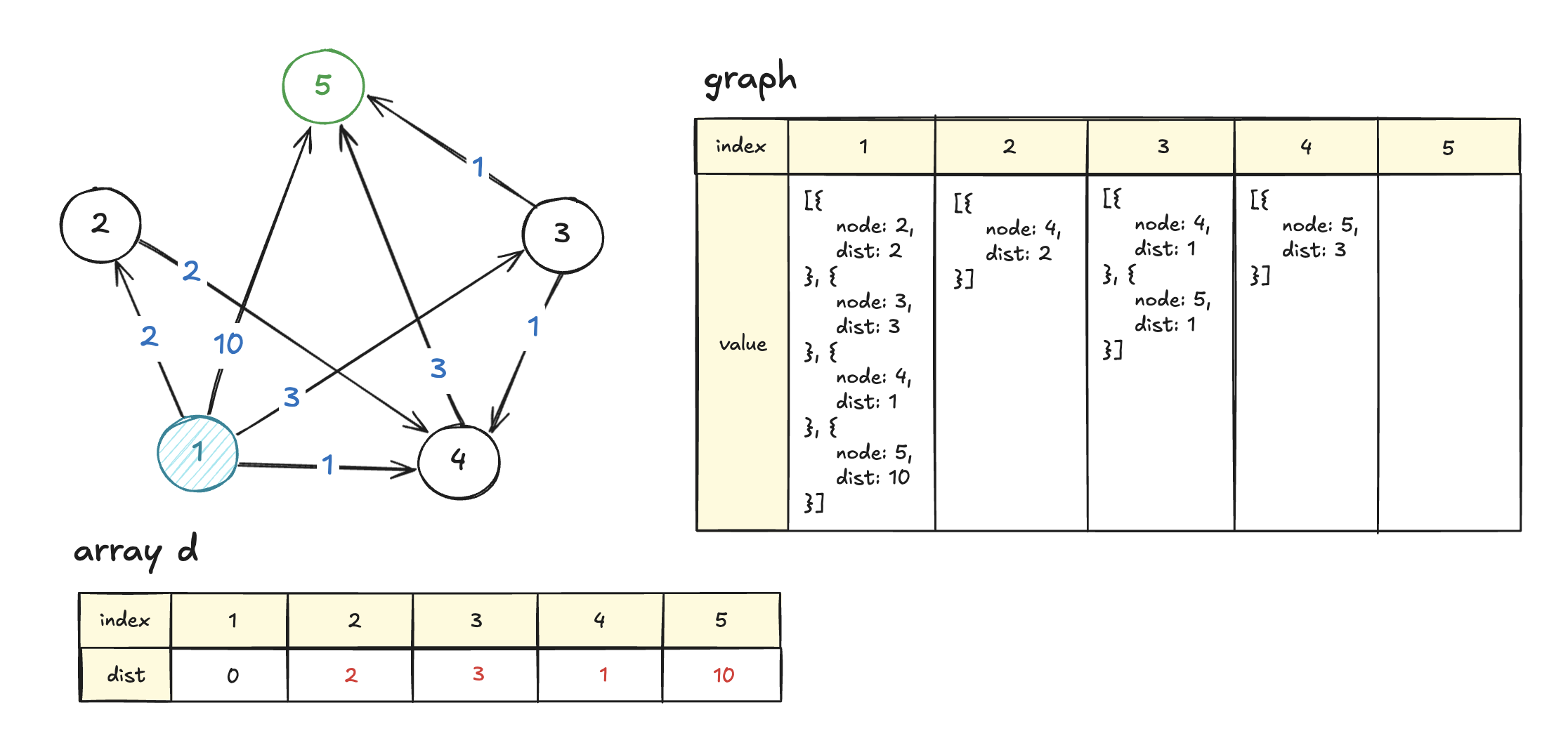
처음은 시작점부터!
시작점 1의 이웃들(graph[1])을 돌며 배열 d를 갱신한다. 그리고 이웃 노드의 정보(node, dist)를 heap에 넣는다.

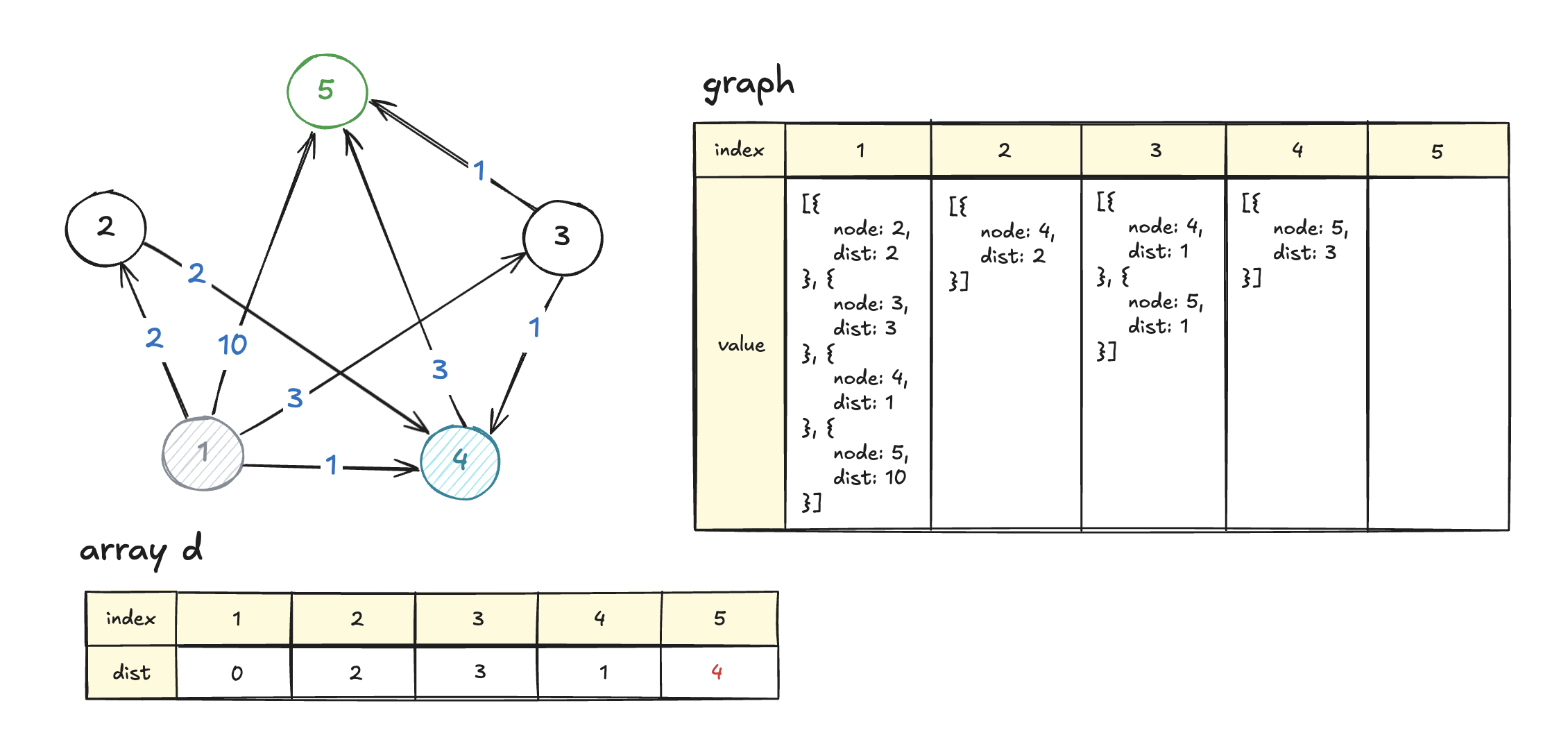
다음으로 배열 d에서 가장 작은 값을 추출한다. (=> minHeap.pop())

여기서는 노드 4가 나올 것이다(dist가 1로 가장 작음).
노드 4의 이웃들(graph[4])을 보는데, 노드 4는 노드 5와 이어져있다.

그러면 시작점에서 5까지 갈 때

시작점에서 나(=4)를 거쳐 5로 가는게 빨라?
- d[4] + 4에서 5로 가는 거리
  = 1 + 3
  = 4
아니면 시작점에서 나(=4) 없이 5로 그냥 가는게 빨라?
- d[5]
  = 10

를 비교하면 된다.

비교해보니 기존의 거리보다 4를 거쳐 5로 가는 것이 더 빠르므로, d[5]를 갱신해주자. 그리고 해당 값을 다시 minHeap에 넣는다.
d[5] = 4
minHeap.insert({node: 5, dist: 4})

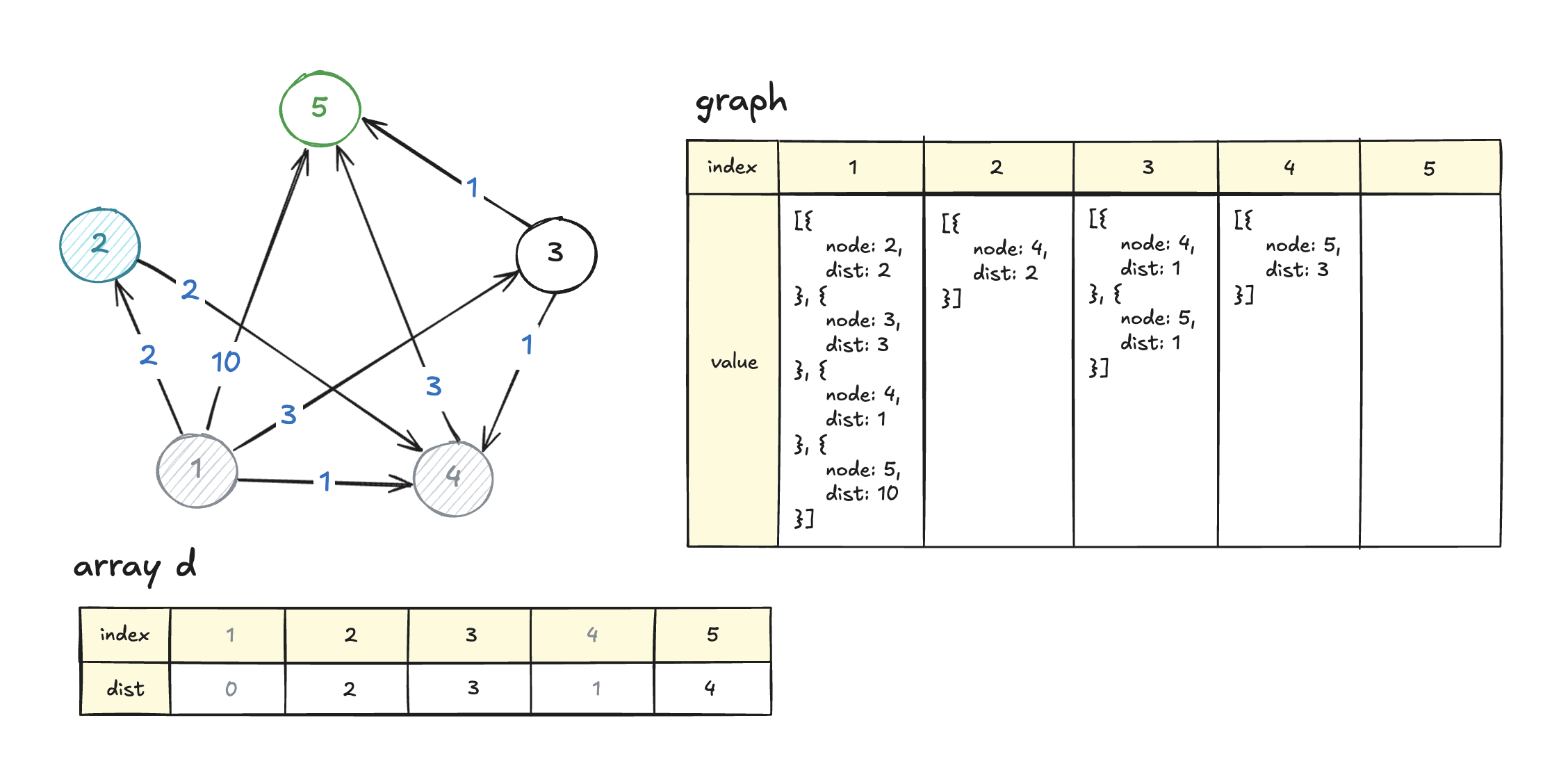
다음으로 가장 작은 노드는 2다.
이 때 노드2의 이웃은 4이다.

그러면 시작점에서 4까지 갈 때,

시작점에서 나(=2)를 거쳐 4로 가는게 빨라?
- d[2] + 2에서 4로 가는 거리
  = 2 + 2
  = 4
아니면 시작점에서 나(=2) 없이 4로 그냥 가는게 빨라?
- d[4]
  = 1

기존의 비용이 더 작기 때문에 건너뛴다.

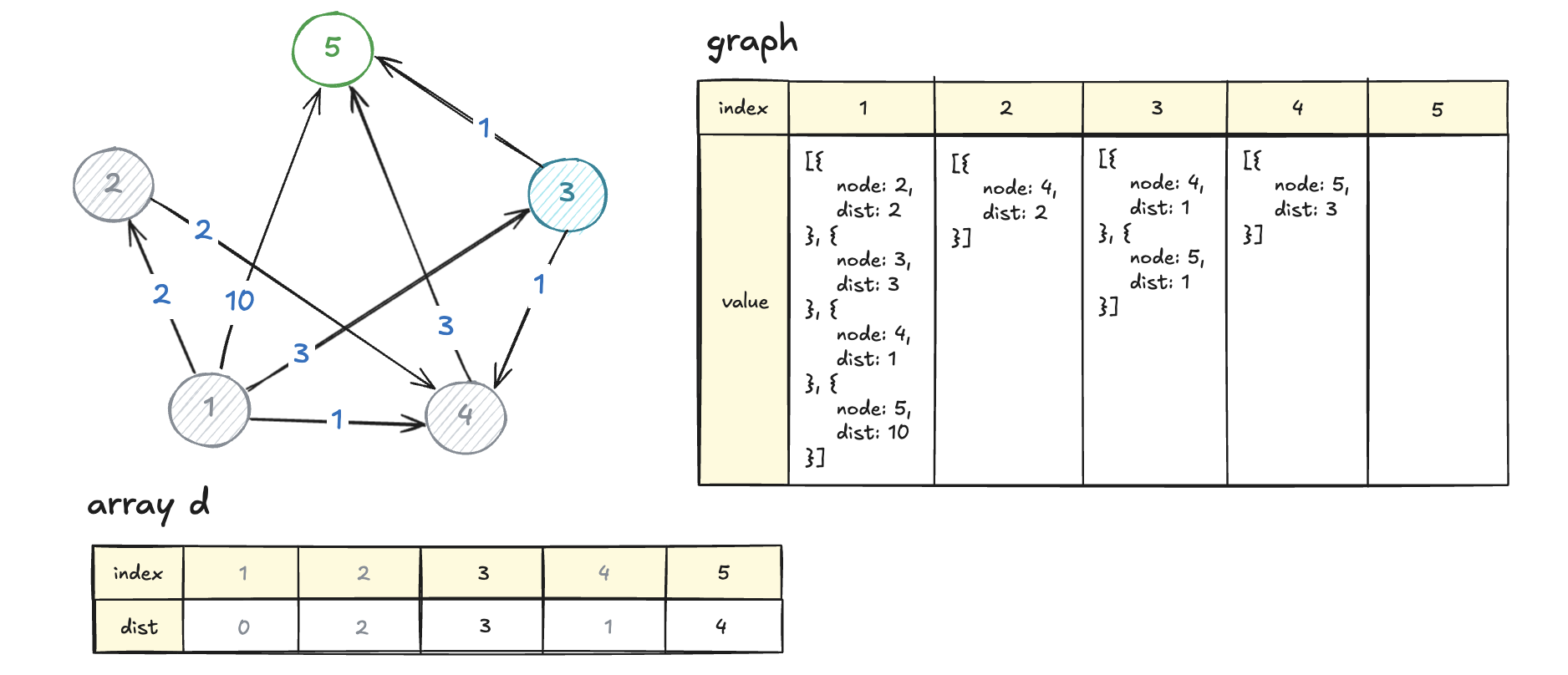
다음으로 가장 작은 노드는 3이다.
3과 이웃한 노드는 4와 5이다.

시작점에서 4까지 갈 때,

시작점에서 나(=3)를 거쳐 4로 가는게 빨라?
- d[3] + 3에서 4로 가는 거리
  = 3 + 1
  = 4
아니면 시작점에서 나(=3) 없이 4로 그냥 가는게 빨라?
- d[4]
  = 1

기존의 비용이 더 작기 때문에 건너뛴다.

시작점에서 5까지 갈 때,

시작점에서 나(=3)를 거쳐 5로 가는게 빨라?
- d[3] + 3에서 5로 가는 거리
  = 3 + 1
  = 4
아니면 시작점에서 나(=3) 없이 5로 그냥 가는게 빨라?
- d[5]
  = 4

이 때도 마찬가지로 기존의 거리와 같으므로 건너뛴다.

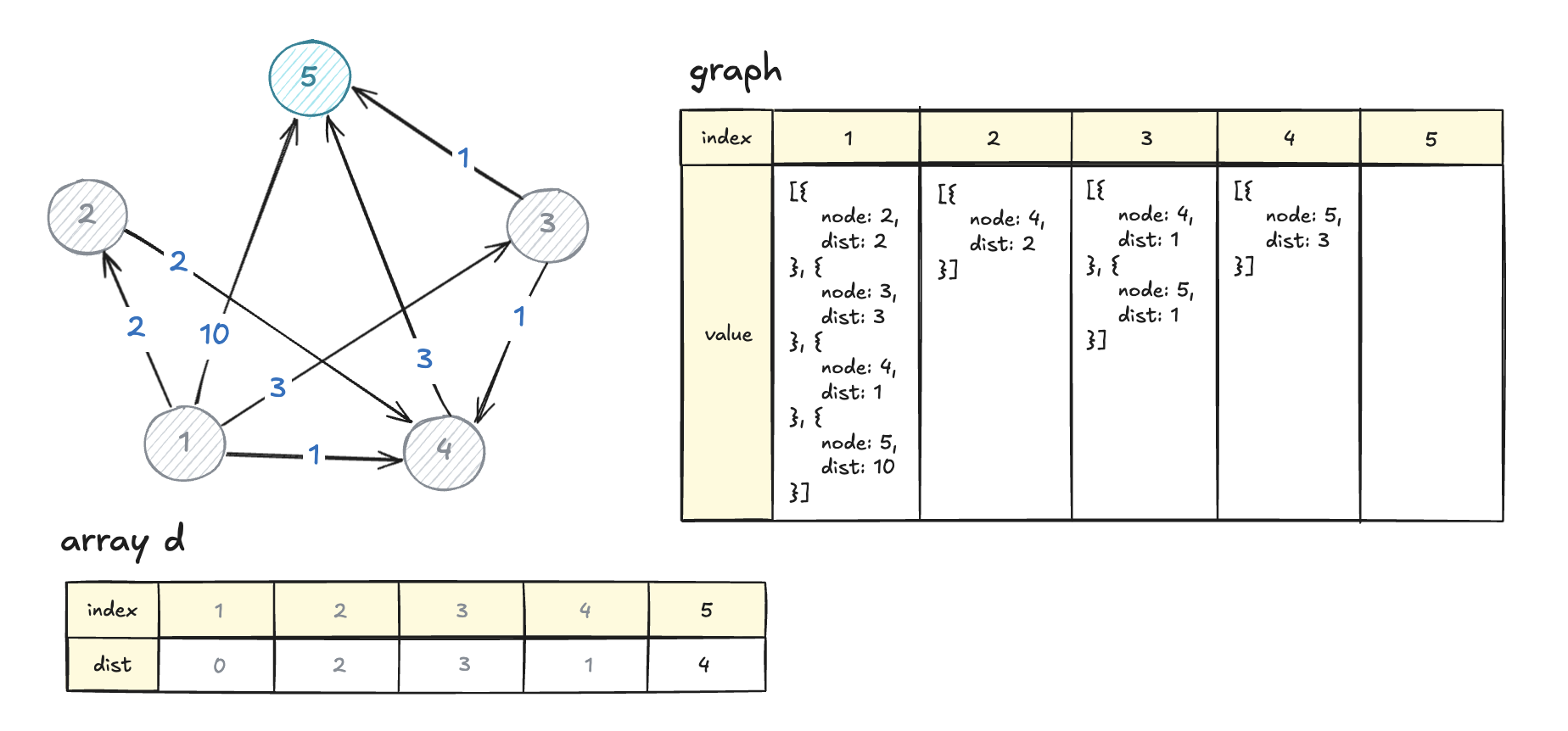
마지막은 노드 5이다. ~~(아자아자!)~~
이 노드 5는 도착점이므로 끝낸다.

전체 코드

백준 문제 1916번의 해답은 다음과 같다.

참고할 부분은, MinHeap 자료구조 구현 부분에서 위에서 설명한 Min Heap 구현과 살짝 다르다.

값의 크기를 비교하는 부분이 다른데, 왜냐하면 insert할 때 {node, dist} 형식으로 데이터를 넣고 있기 때문이다. 값을 비교하는 부분에서 dist 를 기준으로 최소 힙 정렬을 진행한다.

// 최소힙 기반 우선순위 큐
class MinHeap {
  constructor() {
    this.heap = [-1];
  }

  getParentIndex(index) {
    return Math.floor(index / 2);
  }

  getLeftChildIndex(index) {
    return 2 * index;
  }

  getRightChildIndex(index) {
    return 2 * index + 1;
  }

  swap(index1, index2) {
    [this.heap[index1], this.heap[index2]] = [this.heap[index2], this.heap[index1]];
  }

  insert(node) {
    this.heap.push(node);
    this.heapifyUp();
  }

  pop() {
    if (this.heap.length === 1) return null;

    const minNode = this.heap[1];
    const last = this.heap.pop();

    if (this.heap.length > 1) {
      this.heap[1] = last;
      this.heapifyDown();
    }

    return minNode;
  }

  heapifyUp() {
    let index = this.heap.length - 1;

    while (index > 0) {
      const parentIndex = this.getParentIndex(index);
      // dist값을 기준으로 상향식 재정렬 진행
      if (this.heap[parentIndex].dist > this.heap[index].dist) {
        this.swap(parentIndex, index);
        index = parentIndex;
      } else {
        break;
      }
    }
  }

  heapifyDown() {
    let index = 1;
    const length = this.heap.length;

    while (true) {
      const leftChildIndex = this.getLeftChildIndex(index);
      const rightChildIndex = this.getRightChildIndex(index);
      let smallest = index;
		
      // dist값을 기준으로 하향식 재정렬 진행
      if (leftChildIndex < length && this.heap[leftChildIndex].dist < this.heap[smallest].dist) {
        smallest = leftChildIndex;
      }

      if (rightChildIndex < length && this.heap[rightChildIndex].dist < this.heap[smallest].dist) {
        smallest = rightChildIndex;
      }

      if (smallest !== index) {
        this.swap(index, smallest);
        index = smallest;
      } else {
        break;
      }
    }
  }

  isEmpty() {
    return this.heap.length === 1;
  }
}

// 다익스트라
function dijkstra(graph, start, end) {
  const d = new Array(N + 1).fill(Infinity);
  d[start] = 0;

  const minHeap = new MinHeap();
  minHeap.insert({ node: start, dist: 0 });

  while (!minHeap.isEmpty()) {
    const { node: v, dist } = minHeap.pop();

    // 최단 거리가 아니면 무시
    if (dist > d[v]) continue;
    
    // 도착지면 끝
    if (v === end) return dist;

    // 이웃 노드들 확인
    if (graph[v]) {
      for (const { node: w, dist: distW } of graph[v]) {
        const newDist = dist + distW;

        if (newDist < d[w]) {
          d[w] = newDist;
          minHeap.insert({ node: w, dist: newDist });
        }
      }
    }
  }

  return d[end];
}

const inputs = require('fs').readFileSync(0, 'utf-8').trim().split("\n");
const N = +inputs[0];
const M = +inputs[1];
const graph = Array.from({ length: N + 1 }, () => []);
for (let i = 2; i < M + 2; i++) {
  const [v, w, dist] = inputs[i].split(" ").map(Number);
  graph[v].push({ node: w, dist });
}

const [start, end] = inputs[M + 2].split(" ").map(Number);
const answer = dijkstra(graph, start, end);
console.log(answer);

다익스트라 알고리즘의 시간 복잡도는 O(E log V)로, E는 간선의 수, V는 정점의 수를 뜻한다.

문제에서 간선 수는 최대 100,000이고 정점의 개수는 최대 1,000개로 제한했으므로 시간 복잡도를 구하면
O(E log V) = O(100,000 * log 1,000)
log 1,000은 약 10이므로(log 1,000 ≈ 10)
O(100,000 * 10) = O(1,000,000) 이므로 문제를 통과할 수 있다.

꺄!

출처

자료구조: 우선순위 큐(Priority Queue)와 힙(Heap) 10분 핵심 요약

25강 - 다익스트라 알고리즘(Dijkstra Algorithm) [ 실전 알고리즘 강좌(Algorithm Programming Tutorial) #25 ]

김규리

먹바눕

[JS] 최소 힙 구현, 다익스트라 구현 - BOJ 1916 최소비용 구하기

알고리즘

최소 힙

우선순위 큐

힙(Heap) 자료구조 구현

최소 힙

heapify()

데이터 삽입 - 상향식 재정렬, heapifyUp()

데이터 삭제 - 하향식 재정렬, heapifyDown

MinHeap 구현

다익스트라

다익스트라 구현 방법

실전 - 백준 1916. 최소비용 구하기

전체 코드

0개의 댓글