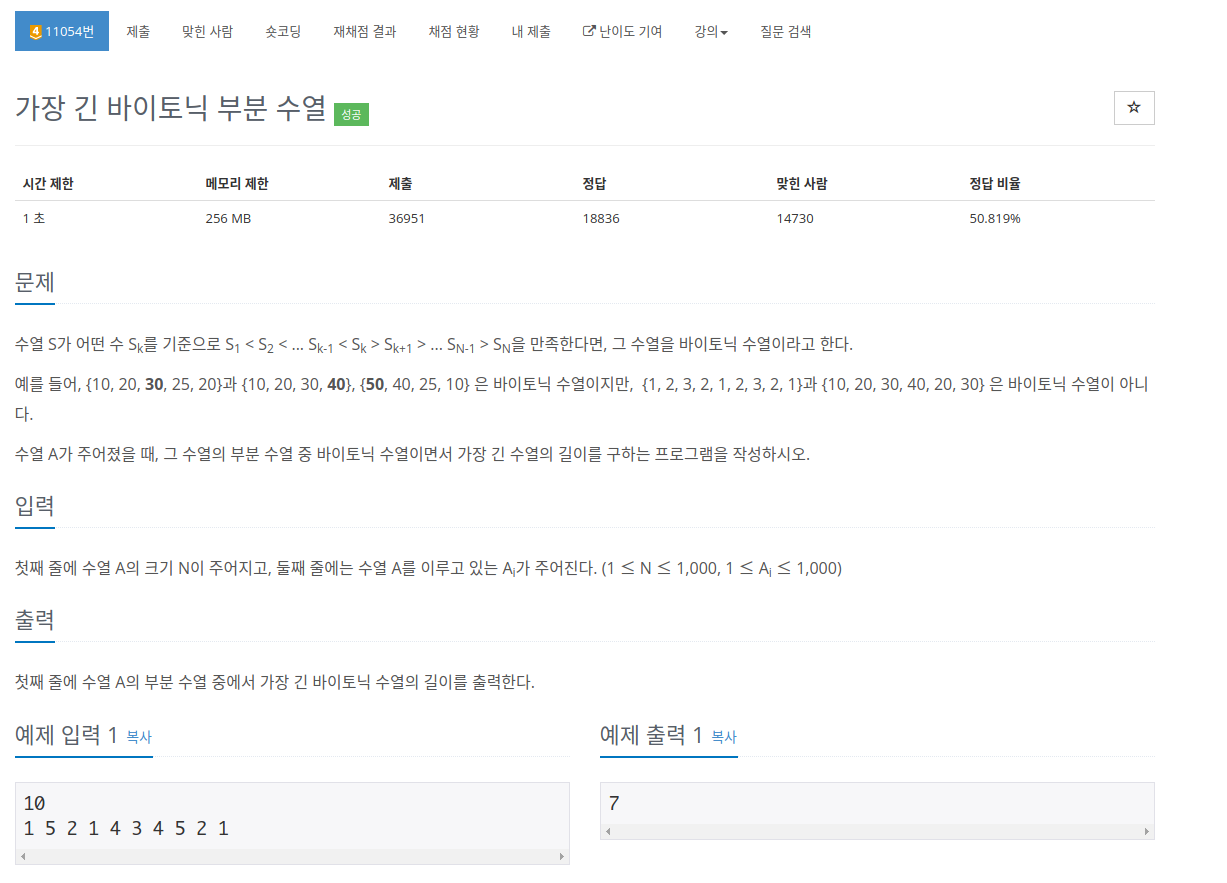
문제

풀이

문제는 어떠한 S(k)를 기점으로 왼쪽은 부분증가수열 오른쪽은 부분감소수열의 최대길이를 출력하는
것인데
먼저 lis 알고리즘을 응용하는 문제라고는 누구나 일단 생각할 수 있을것이다.
(lis알고리즘 링크 -> lis알고리즘이란?)

나의 해결방법은 이렇다.
dp1과 dp2 1차원 리스트인 테이블을 이용하는데
dp1은 각 인덱스를 마지막으로 가지는 증가부분수열의 최대길이를 저장하는 테이블이고

dp2는 각 인덱스를 처음으로 가지는 감소부분수열의 최대길이를 저장하는 테이블이다.

여기서 문제의 핵심이 나오는데
dp1[k] + dp2[k]를 더하면 K를 기점으로하는 가장큰 바아토닉수열의 길이가 된다!!!!

또한 이방법은 lis알고리즘을 2번 시행하기만 하면 되므로
시간 복잡도는 O(N^2)이 된다.

코드

#입력
# 첫째 줄에 수열 A의 크기 N이 주어지고, 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ N ≤ 1,000, 1 ≤ Ai ≤ 1,000)
#예시
# 10
# 1 5 2 1 4 3 4 5 2 1

import sys
input = sys.stdin.readline
INF = int(1e9)

N = int(input())
#수열 S
S = list()
S = list(map(int, input().split()))

#인덱스를 마지막으로 가지는 최고 부분 증가수열의 최대 길이
dp1 = [1] * N

#인덱스를 처음으로 가지는 최고 부분 감소수열의 최대 길이
dp2 = [1] * N
   

for i in  range(1, N):
  for j in range(i):
    if(S[j] < S[i]):
      dp1[i] = max(dp1[i], dp1[j] + 1)

for i in range(1, N):
  for j in range(i):
    if(S[N - 1 - j] < S[N- 1 -i]):
      dp2[N-1-i] = max(dp2[N-1-i], dp2[N-1-j] + 1)


# print('list dp1 : ',dp1)
# print('list dp2 : ',dp2)

result = - 1

for i in range(N):
  tmp = dp1[i] + dp2[i]
  if(result < tmp):
    result = tmp

print(result - 1)