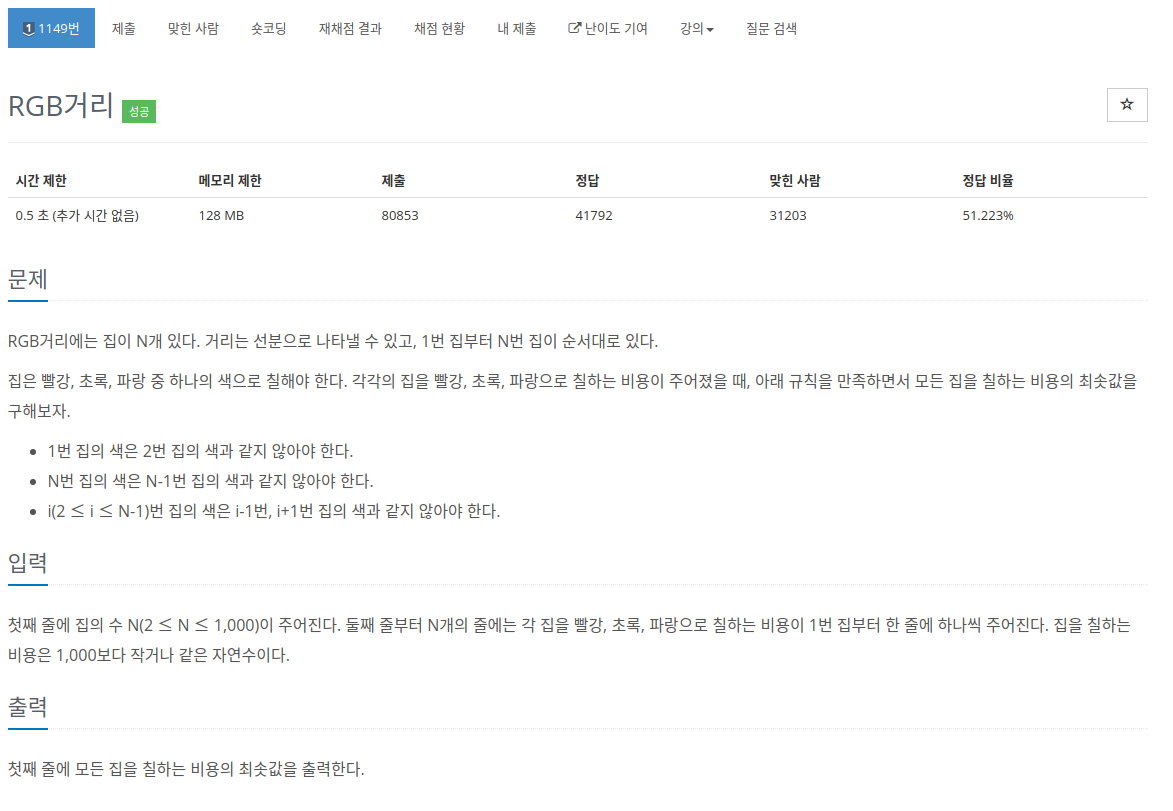
문제

풀이

먼저 이문제는 이전집까지의 최솟값과 다음집의 최솟값과의 관계를 생각하다보니
자연스럽게 dp테이블을 3 X N크기인 2차원 리스트로 만들어야 하고

dp테이블 dp[i][color]는 i번째집에 color색으로 칠했을때 비용의 최솟값을 의미한다

점화식도 자연스럽게 나왔다 문제에서의 조건은 결국 인접한 집에 같은 색깔로 하지말란 뜻이고

따라서 점화식은
dp[i][red] = min(dp[i-1][blue] , dp[i-1][green])
dp[i][blue] = min(dp[i-1][green] , dp[i-1][red])
dp[i][green] = min(dp[i-1][red] , dp[i-1][blue])

코드

코드에 녹여보면

#입력
# 첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나 같은 자연수이다


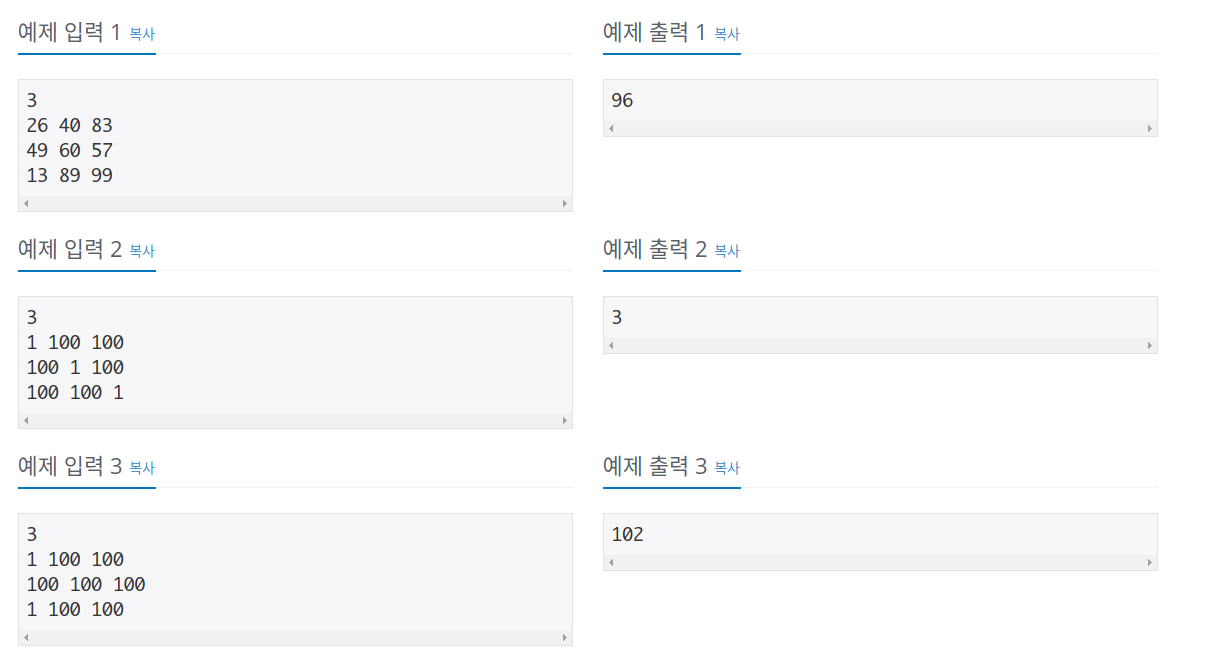
#예제 입력예시)
# 3
# 26 40 83
# 49 60 57
# 13 89 99

#출력 예시)
#96

#점화식
# d[i][0] = min(d[i-1][1] , d[i-1][2] )
import sys

N = int(sys.stdin.readline().rstrip())

color = list()


for i in range(N):
  color.append(list(map(int, sys.stdin.readline().split())))

dp = [[0] * 3 for _ in range(N)]
dp[0][0] = color[0][0]
dp[0][1] = color[0][1]
dp[0][2] = color[0][2]

#바텀업 방식으로 dp채우기

for i in range(1, N):
  
  dp[i][0] = min(dp[i-1][1], dp[i-1][2]) + color[i][0]
  dp[i][1] = min(dp[i-1][0], dp[i-1][2]) + color[i][1]
  dp[i][2] = min(dp[i-1][0], dp[i-1][1]) + color[i][2]
  


print(min(dp[N-1]))