문제

풀이

문제 설명
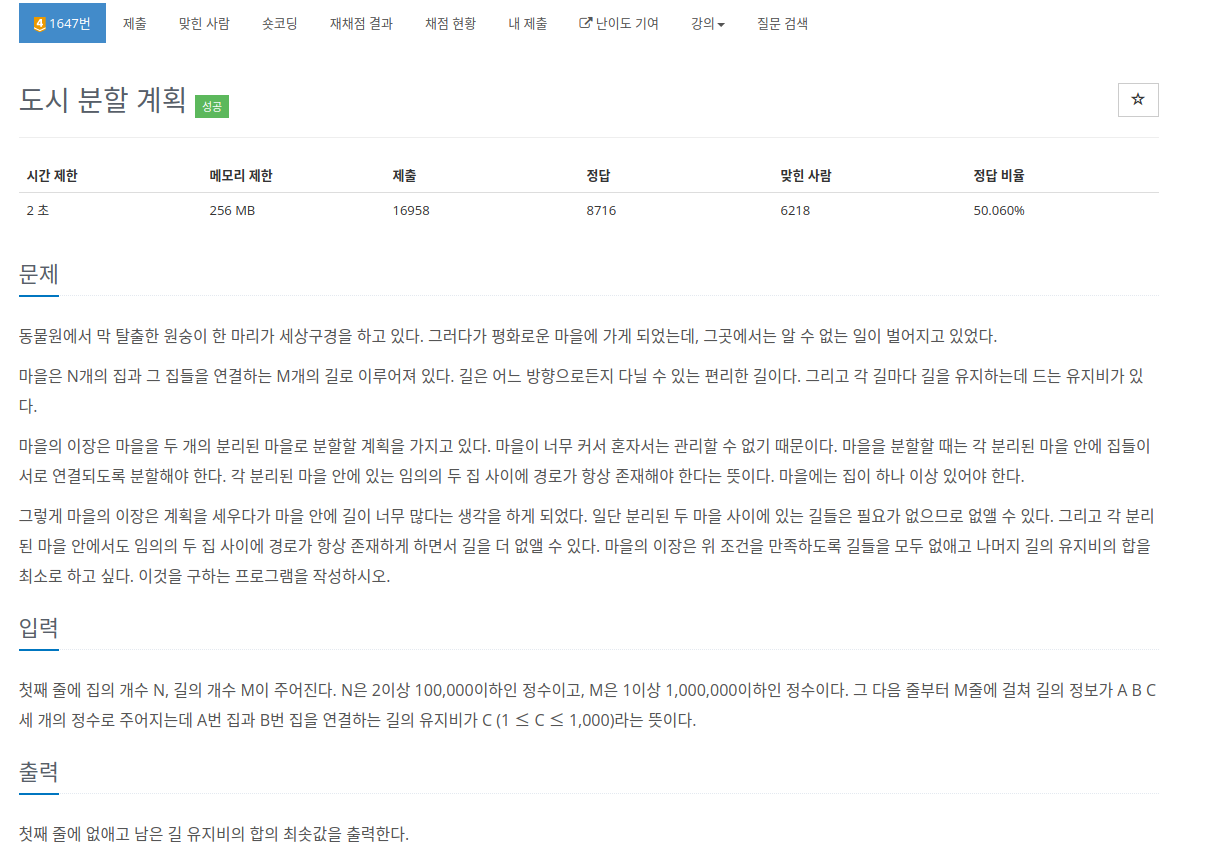
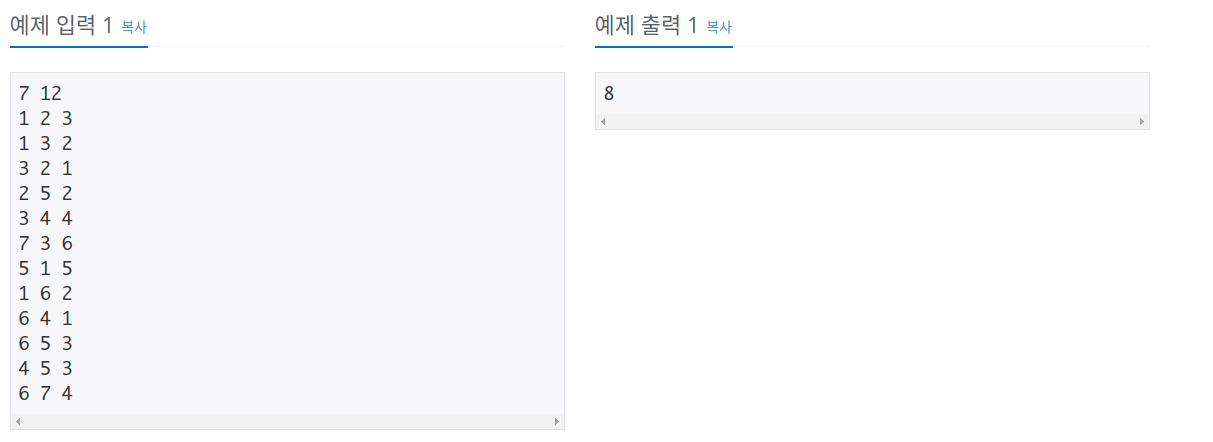
N개의 집(노드)와 M개의 방향성이 없는 길(간선)이 있는 마을이 있다.
마을 이장은 마을을 2개로 분할할 것이다.
또한 분할된 각 마을은 서로 연결되어 있으며 임의의 두 마을을 선택했을 때 항상 경로가있다.
(신장트리로 볼 수 있다!!!)

이 때 두개로 분할한 마을이 최소 신장트리가 된다면 문제의 조건을 만족한다.

idea : 최소 스패닝트리에서 가장 비용이큰 간선 1개를 없앤다.
내 방법을 간소화하면

1. 전체 그래프를 신장트리로 만든다.
2. 그 만든 신장트리중 가장 비용이 큰 간선을 없앤다.

코드

import sys
input = sys.stdin.readline

def find_parent(parent, x):
  if(x != parent[x]):
    parent[x] = find_parent(parent, parent[x])
    return parent[x]
  return x
  
def union_parent(parent, a, b):
  a = find_parent(parent,a)
  b = find_parent(parent,b)
  if a < b:
    parent[b] = a
  else:
    parent[a] = b

V, E = map(int, input().split())
edges = []

for _ in range(E):
  a, b, c = map(int, input().split())
  edges.append((c, a, b))

parent = [0] * (V+1)
for i in range(1, V+1):
  parent[i] = i
#크루스칼 알고리즘
max_cost = -1
result = 0
edges.sort()
for edge in edges:
  cost, a, b = edge
  if(find_parent(parent, a) != find_parent(parent, b)):
    union_parent(parent, a, b)
    max_cost = max(max_cost, cost)
    result += cost

result -= max_cost
print(result)