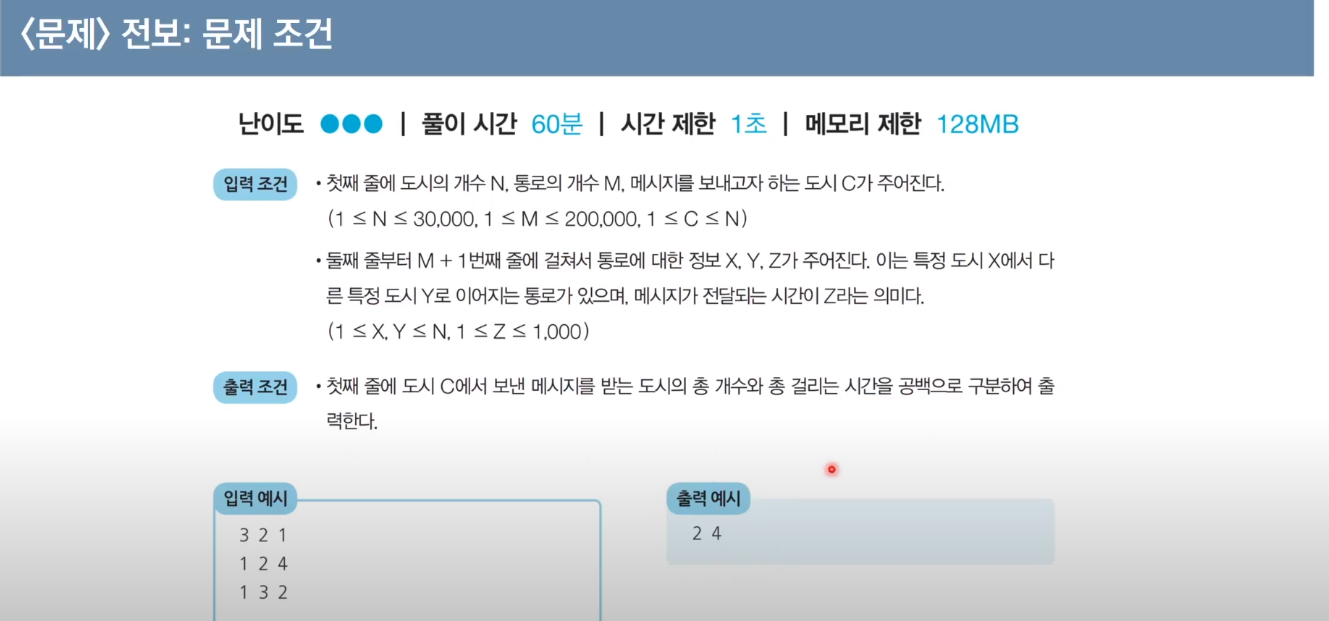
문제

풀이

먼저 이문제에서는 읽었을 때 알 수 있듯이 방향성이있는 간선을 가지는 방향 그래프이고
특정 한 지점에서 갈 수 있는 도시의 수 result1과 메세지가 다 전달되는시간 즉
특정 한 지점에서 갈 수 있는 도시들중 최고 비용인 result2를 출력해주면 된다.

그렇다면 한지점에서의 최단경로를 구하는 다익스트라 알고리즘으로 이 문제를 해결할 수 있고
나머지는 구현문제가 된다.

코드

#input sample
# 3 2 1
# 1 2 4
# 1 3 2
#첫째 줄에는 도시의 개수 N 통로의개수 M 메세지를 보내고자 하는 도시 C가 주어진다.
#둘째 줄부터 M+1줄까지는 간선의 정보가 주어지는데 출발도시 X 도착도시 Y 비용 Z가주어진다.

import sys
import heapq
input = sys.stdin.readline

INF = int(1e9)

N, M, C = map(int, input().split())
graph = [[] for _ in range(N+1)]
distance = [INF] * (N+1)

for _ in range(M):
  X, Y, Z = map(int, input().split())
  graph[X].append((Z, Y))


def dijakstra(start):

  q = []
  heapq.heappush(q, (0, start))

  while q:

    dis, cur = heapq.heappop(q)
    if(dis > distance[cur]):
      continue

    for j in graph[cur]:
      cost = dis + j[0]
      if(distance[j[1]] > j[0]):
        distance[j[1]] = j[0]
        heapq.heappush(q, (cost, j[1]))  
    
  
dijakstra(C)

result1 = 0
result2 = 0
max = -1

for i in range(N+1):
  if(distance[i] != INF and distance[i] != 0):
    result1 += 1
    if(distance[i] > max):
      max = distance[i]


result2 = max

print(result1, result2)