차원 축소 기법인 주성분 분석과 요인 분석의 차이는 무엇인지 설명해 주세요.
차원 축소란?
차원 축소는 매우 많은 피처로 구성된 다차원 데이터 세트의 차원을 축소해 새로운 차원의 데이터 세트를 생성하는 것이다.
일반적으로 차원이 증가할수록 데이터 간의 거리가 기하급수적으로 증가하기 때문에, 희소한 구조를 가지게 되고 모델의 예측 신뢰도가 떨어지게 된다.
따라서 차원 축소를 할 경우 학습 데이터의 크기가 줄어들어서 학습에 필요한 처리 능력도 줄일 수 있다.
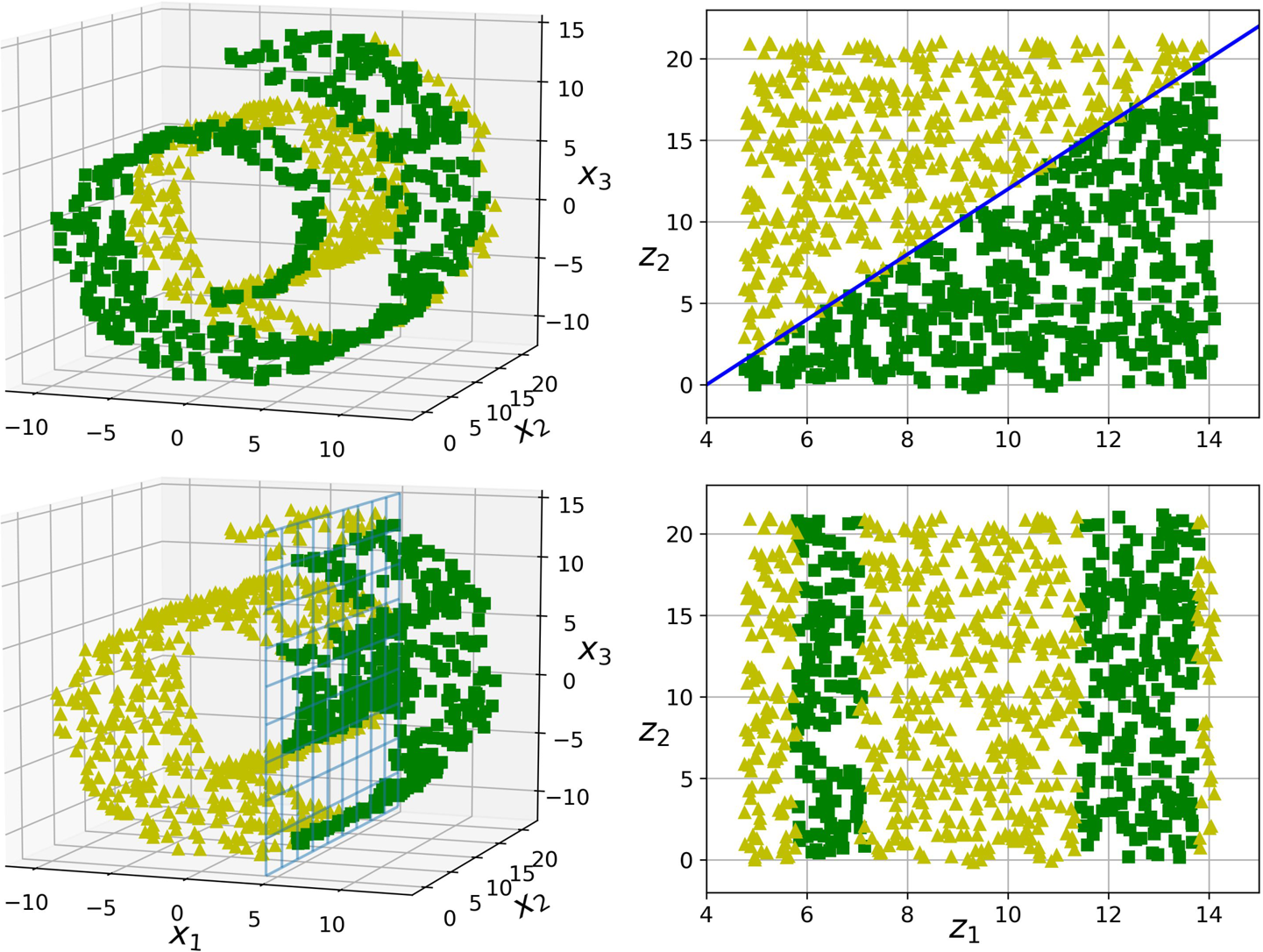
차원 축소는 크게 두 가지 접근 방식으로 구분된다.
바로 기존의 변수들을 결합하여 새로운 저차원의 변수 집합을 만들어내는 특징 추출과, 변수들 중에서 중요한 변수만 선택하고, 덜 중요한 변수는 제거하는 특징 선택이 있다. 오늘 이 글에서 설명할 주성분 분석과 요인 분석은 모두 특징 추출에 해당하는 기법이다.
1. 주성분 분석(PCA)란?
우선 주성분 분석(PCA)는 가장 대표적인 차원 축소 기법이다. 여러 변수 간에 존재하는 상관관계를 이용해 이를 대표하는 주성분을 추출해 차원을 축소하는 방식으로 동작한다.
PCA 기법의 핵심은 데이터를 축에 비추어 봤을 때 가장 높은 분산을 가지는 데이터의 축을 찾아 그 축으로 차원을 축소하는 것인데, 이 축을 "주성분"이라고 말한다. 높은 분산을 가지는 축을 찾는 이유는 정보의 손실을 최소화하기 위함이다.
데이터를 축에 비추어 봤을 때 분산이 크다는 것은 원래 데이터의 분포를 잘 설명할 수 있다는 것을 뜻하고, 정보의 손실을 최소화 할 수 있다는 것을 뜻한다.
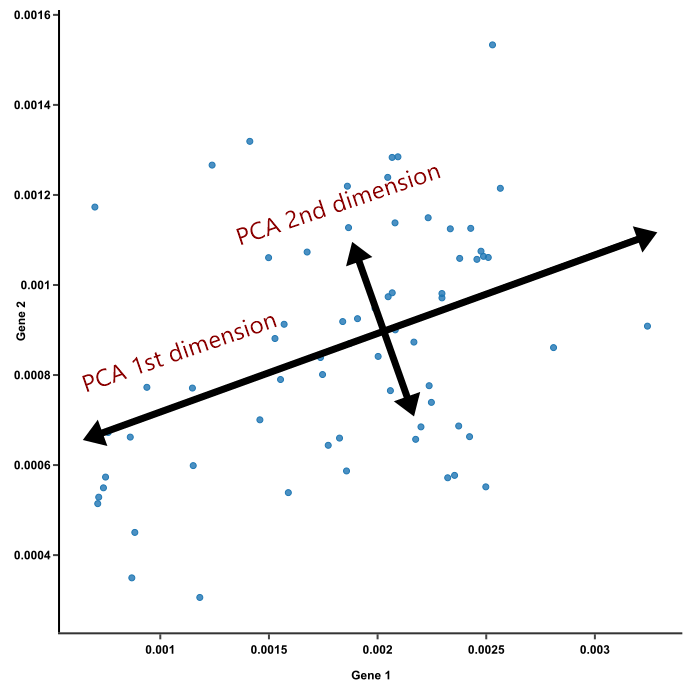
PCA는 제일 먼저 가장 큰 분산을 기반으로 첫 번째 축을 생성하고, 두 번째 축은 이 벡터 축에 직각이 되는 벡터를 축으로 한다. 첫 번째 주성분은 전체 데이터의 분산을 가장 많이 설명하고, 두 번째 주성분은 남은 분산을 설명하는 방식으로 진행되는 것이다.
이렇게 생성된 벡터 축에 원본 데이터를 투영하면 벡터 축의 개수만큼의 차원으로 원본 데이터가 차원 축소된다.
주성분은 데이터의 선형 결합으로 정의되며, 특정 변수 간의 관계나 잠재 요인을 직접적으로 해석하지는 않는다. 즉, 데이터의 구조를 간결하게 표현하는 데 초점을 맞춘다는 것이다.
2. 요인 분석이란(Factor Analysis)?
요인 분석(FA)는 여러 관찰된 변수들 간의 상관관계를 분석하여, 이들 뒤에 숨겨져 있는 잠재 요인(Latent Factors)을 찾아내는 기법이다. 변수 간의 공통된 상관성을 설명하는 잠재적인 요인을 도출하고, 변수들의 공통 요인 구조를 밝히는 데 중점을 둔다.
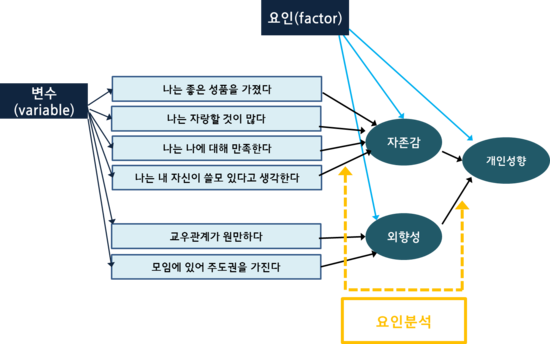
FA에서는 우선 관찰된 변수들이 공통적으로 영향을 받는 숨겨진 요인(공통 요인)을 도출한다. 예를 들어, 학생의 시험 점수에서 "지능"과 "성실성" 같은 잠재 요인을 추출하는 것이다. 이를 위해 관찰된 변수들 간의 상관관계를 분석하고, 잠재 요인이 데이터의 공통된 패턴을 얼마나 잘 설명하는지를 평가한다.
이후 변수의 개수를 줄이면서, 데이터의 핵심적인 공통된 정보를 유지한다. 이 과정에서 고유값 등을 활용하여 요인의 개수를 결정하며, 요인의 해석 가능성을 높이기 위해 회전 방식을 적용한다. 마지막으로 변수들 간의 상관관계를 단순화하고, 공통된 특성을 그룹화하여 각 요인의 의미를 해석한다.
- 회전(rotation): 공통 요인을 더 해석하기 쉽게 만들기 위해 요인 축을 조정하는 과정이다.
결론적으로 "주성분 분석"은 데이터의 전체 분산을 고려하여 차원을 축소하는 반면, "요인 분석"은 공통 요인을 도출하는 데 초점이 있고, 관찰된 변수의 원인을 설명하려고 하는 것이 차이이다.
