Hashing(충돌 처리) - Chainless(Linear probing, Linear Quotient, Brent’s Method)

gyumin.park·2023년 11월 14일

목록 보기

3/3

Chainless Hashing

Chain을 명시적으로 표시하는 link field를 사용하지 않는다.

Hash table에는 주소마다 오직 하나의 record만 저장한다.

동일 HA를 가지는 record를 가진 주소들을 찾아가는 방식이 존재한다.

Hash table 전체를 열린 공간으로 가정하고 HA가 충돌하면 빈 자리의 주소가 될 때까지 HA를 계속 만들어 낸다.
-> Open Addressing(개방주소법)이라고 부름

속도는 느린대신 공간을 덜 사용(link field 없음)

Table size: 항상 소수

Linear probing(선형 조사)

Chainless 중 가장 단순한 방법
HA에 이미 다른 레코드가 입력되있으면(충돌) 현재 주소에서 고정 폭으로 다음 주소로 이동하여 빈 자리가 발견되면 그곳에 저장
step size (sz)를 특정 자연수로 놓음

Insertion

넣을 레코드의 HA를 h라고 할 때 h0 = h, h1 = h0 + sz
h0이 빈자리인지 확인
비어 있다면 record를 h0에 삽입
비어 있지 않다면 h1이 빈 자리인지 확인
h0에 다시 도달하면 insertion실패(hash table 꽉 참)

Retrieval

찾을 레코드의 HA값에서 출발해 insertion처럼 probe sequence를 가정
probe sequence를 차례로 조사

Deletion

삭제할 레코드를 검색 후, 그 자리를 빈 자리(NULL)로 초기화 하면 안 됨
NULL 대신 "tombstone"이라는 indicator 사용
- tombstone 자리에 삽입이 일어나면 해당 위치의 indicator 제거

Linear Quotient(Double Hashing)

2개의 해시 함수 사용
Hash function H1 : key값을 hash table의 HA로 변환
Hash function H2 : 충돌 발생 시 다음 위치를 위한 step size를 구한다.
record들이 각자의 H2를 가지므로 probe sequence가 동일하지 않음
-> Linear probing의 개선된 방법으로 secondary clustering 문제를 해결

Secondary clustering: 2개 이상의 record가 동일한 probe sequence를 가지는 것

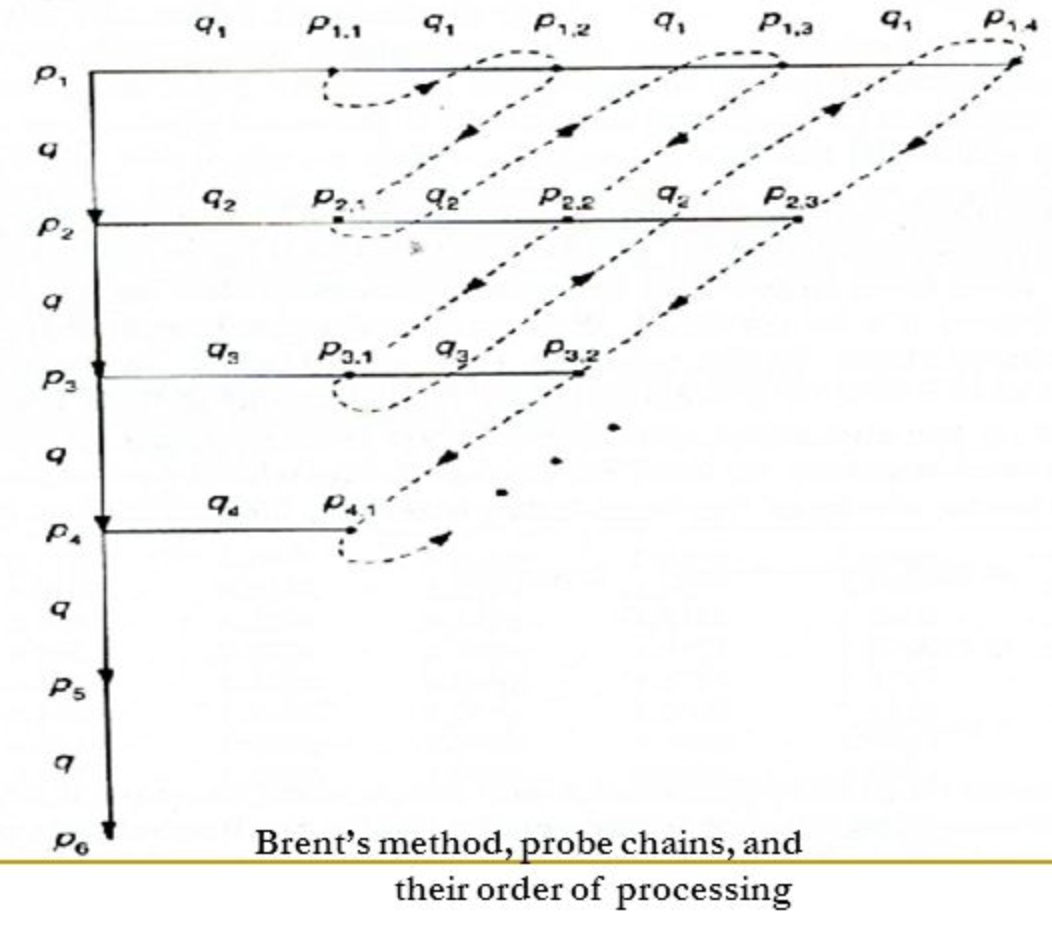
Brent's Method

Linear Quotient 기법을 개선한 기법
- 삽입할 레코드의 primary probe chain 상의 레코드를 다른 곳으로 이동시키고 그 자리에 삽입
- Linear Quotient 기법보다 retrieval 시 probe 수 감소
삽입할 레코드의 key값을 k, H1(k)=h, H2(k)=q 라 하자
Primary probe chain
- p1 = h, p2 = h + q, p3 = h + 2q
- Linear Quotient 기법이 조사하는 주소들임
Secondary probe chain
- Primary probe chain 상의 어느 위치 pi에 대해 생각해보자
- pi에 이미 들어있는 레코드의 key값을 B, H2(B)=qi 라고 하자
- B를 이동시킬 수 있는 위치의 sequence를 secondary probe chain 이라고 함
- pi,1 = pi + qi, pi,2 = pi,1 + qi, ...

Improved Brent Method

Complete Binary Tree를 이용하여 Brent's method를 개선한 기법
Brent method에서는 PPC상의 레코드들이 이동 대상이 된다.
new Brent method에서는 SPC상의 레코드들도 이동 대상이 된다.
일반화된 기법을 구현하기 위해 완전 이진 트리를 사용한다.
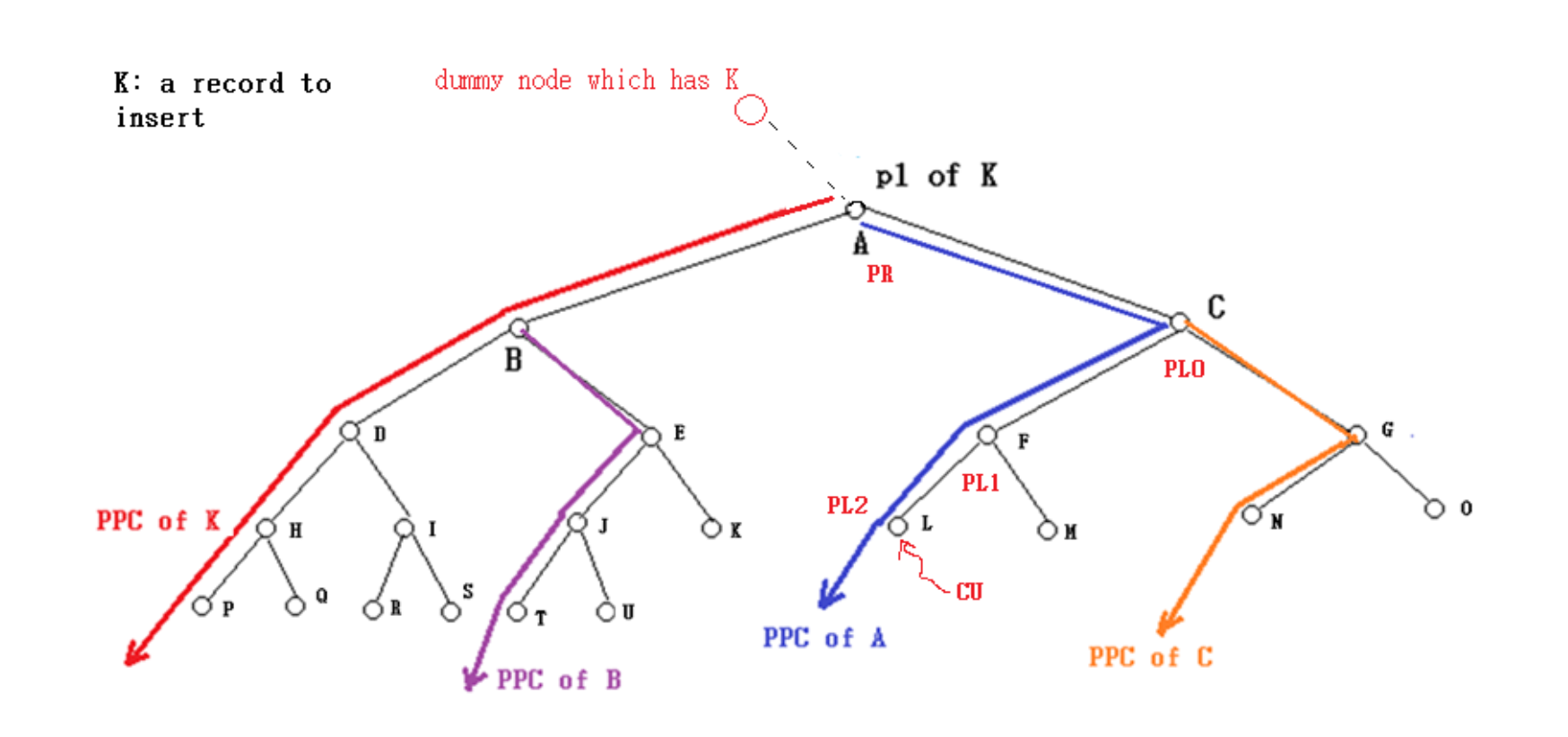
완전 이진 트리의 노드들은 1번부터 시작하여 번호 순으로 차례로 하나씩 생성됨(1번은 root노드)
마지막에 생성된 노드에 해당하는 hash table의 주소가 비어 있다면, 더 이상의 노드 생성을 중지함
각 노드는 hash table의 한 주소로 대응됨
임의의 노드마다 자신을 PR로 하는 노드들의 열을 생각할 수 있음
제일 먼저 root 노드에게 삽입할 레코드의 home address를 대응시킴
이 주소를 출발점으로 이후에 생성되는 각 노드에 hash table의 주소를 대응시킬 수 있음
지금 생성된 임의의 노드를 cu라 부르자. 그러면 이 노드에 대응하여 PL0, PR 노드가 존재함
- PL0 : cu에서 left-child 포인터만 따라 올라가서 나오는 마지막 노드. 한 번도 올라갈 수 없다면 cu가 PL0 임
- 여기서 거치는 노드를 역순으로 하여 PL0, PL1, ..., PLi(=cu)라 부르자
- PR : PL0에서 right-child 포인터를 한 번 따라 올라가서 나오는 노드
- 주 : root 노드는 dummy node의 right-child라고 간주함
결국 cu에 대응된 주소는 cu의 PR에 저장된 레코드의 PPC의 한 원소의 주소임
- cu가 PL0라면, cu의 주소 = PR의 주소 + increment of record in PR
- cu가 PLi라면(i > 0), cu의 주소 = PLi-1의 주소 + increment of record in PR