프로그래머스 | 점 찍기

📍문제 설명📍

좌표평면을 좋아하는 진수는 x축과 y축이 직교하는 2차원 좌표평면에 점을 찍으면서 놀고 있습니다. 진수는 두 양의 정수 k, d가 주어질 때 다음과 같이 점을 찍으려 합니다.

• 원점(0, 0)으로부터 x축 방향으로 ak(a = 0, 1, 2, 3 ...), y축 방향으로 bk(b = 0, 1, 2, 3 ...)만큼 떨어진 위치에 점을 찍습니다.
• 원점과 거리가 d를 넘는 위치에는 점을 찍지 않습니다.
  예를 들어, k가 2, d가 4인 경우에는 (0, 0), (0, 2), (0, 4), (2, 0), (2, 2), (4, 0) 위치에 점을 찍어 총 6개의 점을 찍습니다.
  
  정수 k와 원점과의 거리를 나타내는 정수 d가 주어졌을 때, 점이 총 몇 개 찍히는지 return 하는 solution 함수를 완성하세요.

---

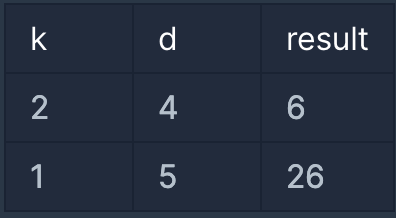
📚입출력 예시📚

---

❌실패한 풀이❌

function solution(k, d) {
    var answer = 0;
    for(let i = 0; i <= d; i += k) {
        for(let j = 0; j <= d; j += k) {
            if(Math.sqrt(i**2 + j**2) <= d) answer++;
        }
    }
    return answer;
}

---

💯성공한 풀이💯

function solution(k, d) {
    var answer = 0;
    for(let i = 0; i <= d; i += k) {
        let y = parseInt(Math.sqrt(d**2 - i**2))
        
        answer += parseInt(y / k) + 1
    }
    return answer;
}

💡문제 접근 방식💡

문제의 제한조건이 1,000,000까지이기 때문에 당연히 시간초과가 날 것이라고 생각했다.

그렇다면 이 문제는 시간복잡도가 O(n)이나 더 안정적인것으로 풀어야한다는 소리이다.

수학적으로 생각하면 원점과 한점은 원의 반지름이 될 수 있다.
그렇다면 반지름이 d인 원을 생각해보면 된다.
원의 방정식은 r^2 = (x-a)^2 + (y-b)^2 이므로
x를 좌변으로 넘기면 y 좌표를 구할 수 있다.
r^2 - (x-a)^2 = (y-b)^2 여기서는 원점과의 거리였기 때문에
r^2 - x^2 = y^2 으로 y 좌표를 도출 할 수 있다.
y가 또한 k의 배수이기때문에 k로 나누어주고 원점을 포함해야하기때문에 +1 을 해준다.