https://medium.com/@abby.s.mitchell/getting-started-with-qiskit-explained-by-a-software-developer-not-a-quantum-physicist-b8ba820685e5 / abby mitchell

이 글은 외국의 개발자분이 초보자를 위해 Qiskit 튜토리얼을 작성하신 것을 번역하였습니다. 정말 좋은 자료라 한국어로 번역하여 많은 분들이 읽으시면 좋겠는 마음에 원작자에게 허락을 구했더니 흔쾌히 번역을 허락해주셨습니다 다시 한번 감사드려요! (Abby, Thank you again!)
저와 개발자 친구 피터가 번역하였고 신소영(sophy.shin@kakao.com)님이 검수해주셨습니다 :)

Qiskit 시작하기 (물리학자말고 소프트웨어 개발자가 설명해줄게)

양자컴퓨팅에 관심이 있는 소프트웨어 개발자인데, 고등학교 때부터 물리학을 공부하지 않았다고요? IBM의 퀀텀 코드베이스(Qiskit)를 사용해 보고 싶지만, 어디서부터 시작해야 할지 모르겠다고요? 몇 개의 블로그나 튜토리얼을 찾았지만, 전문 용어 때문에 꼼짝 못하고 있진 않나요?
여러분은 운이 좋습니다. 저는 이미 위와 같은 어려움을 겪었고 여러분은 그런 과정을 겪지 않도록 이 블로그를 쓰기로 하였습니다.

이 튜토리얼을 안내해 드리겠습니다 : Getting Started with Qiskit (https://github.com/Qiskit/qiskit-tutorials/blob/master/tutorials/circuits/1_getting_started_with_qiskit.ipynb)

저는 양자물리학자가 아닙니다. 이 블로그의 목표는 튜토리얼의 개념에 대한 매우 수준 높은 개요를 제공함으로써 더 많은 소프트웨어 개발자들이 양자컴퓨팅을 시작할 수 있도록 돕는것입니다. 여러분이 쓰는 코드를 이해하는데 도움이 되는 아주 기본적인 필요한 지식을 알려드리겠습니다. 만약 여러분이 이 블로그에서 다루는 지식 이상으로 양자컴퓨팅을 다루고 싶다면, 아마도 어느 시점부터는 조금 더 깊이 있는 양자물리학 이론을 배워야할지도 모릅니다 (미안해요!)

시작하기에 앞서 (중요!)

여러분이 양자컴퓨팅에 대한 기본 지식이 있고, 기존 컴퓨팅과 어떻게 비교되는지 알고 있다고 가정합니다. 만약 큐비트(qubits), 얽힘(entanglement), 중첩(superposition)이 무엇인지 모른다면 여기서 기본을 다지는 것을 제안합니다 (기다릴테니 다녀오세요):

https://www.youtube.com/watch?v=JhHMJCUmq28&feature=youtu.be

여기서 사용된 실제 코드 아주 복잡하지 않기 때문에 그저 일반적인 프로그래밍 지식만으로 충분하긴 하겠지만 여러분이 파이썬에 대한 지식을 어느 정도 가지고 있다고 가정합니다.
튜토리얼을 진행하기 위해 Qiskit을 설치해야 하는데, 만약 아직 설치하지 않았다면 다음의 동영상을 따라 설치해 보세요.

https://www.youtube.com/watch?v=M4EkW4VwhcI&feature=youtu.be

Qiskit을 설치했다면 빈 주피터 노트북을 열고 시작할 수 있습니다!
(설치 파일은 다음의 링크를 확인하세요: https://www.qiskit.org/overview#quick-start)

Tutorial Part 0 — Qiskit 시작하기

튜토리얼 Part 0: Qiskit 시작하기

좋아요, 첫 번째 단원부터 시작합시다.
만약 다음과 같이 생긴 시각화된 양자 회로를 본 적 없다면:

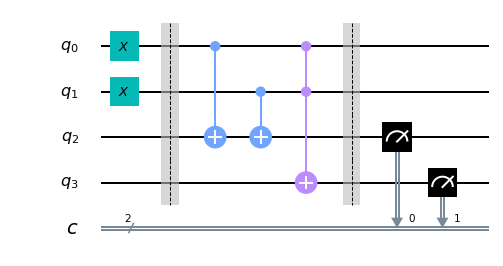
사용 중인 라이브러리에 따라 다른 스타일의 형태 봤을 수도 있습니다. 위의 시각화는 Qiskit을 통해 얻은 스타일화된 버전이며, 코드의 결과물로 다음과 같은 조잡한 버전도 볼 수 있습니다:

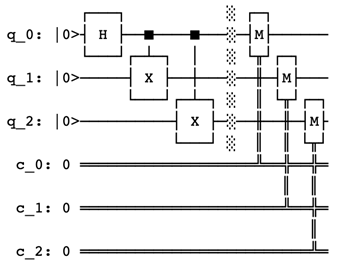
간단히 말하자면, 양자 컴퓨터로 알고리즘을 수행하는 것은 다음과 같은 과정을 포함합니다:
지정된 수의 큐비트를 시스템(예. 회로)에 전달합니다.
(알고리즘을 구성하는) 지정된 게이트 조합을 해당 큐비트에 적용합니다.
큐비트를 측정하고 그 결과를 고전적인 비트(예. 0과 1)로 저장합니다.

위에서 본 시각화된 회로를 다시 살펴 봅시다:

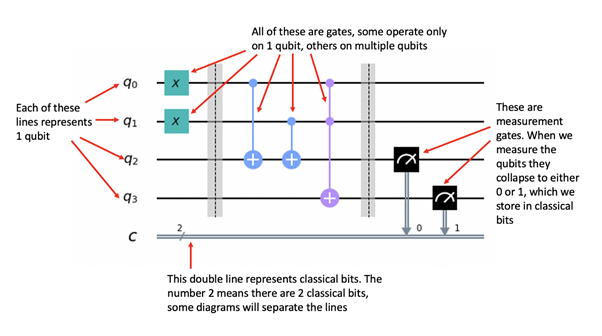
어떤 결과를 측정하기 전에 실제로 그 회로를 설정해야 합니다(이것을 빌드 단계라고 합니다). 그러고나서 양자 컴퓨터 시뮬레이션 혹은 실제 컴퓨터에서 (실행 단계라고 알려진) 실험을 실행합니다. 이 단계를 구현하기 위해 Qiskit 코드를 사용합니다.
큐비트에 적용할 수 있는 다양한 게이트들이 있는데 이 튜토리얼의 목적을 위해서는 두 개만 알면 충분합니다:

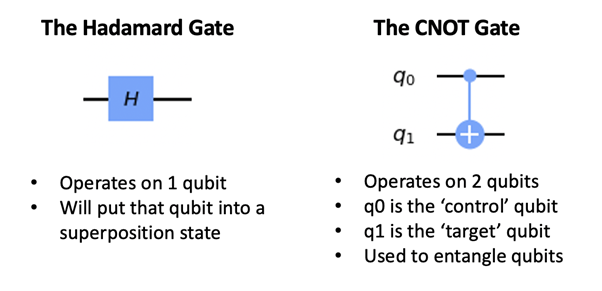
Tutorial Part 1 — 회로 만들기

괜찮아요 당황하지 마세요. 전문용어가 많기는 하지만 천천히 따라와 보세요.
세 큐빗 GHZ 상태란 무엇일까요?

이것은 얽혀있는 3개 큐비트 세트를 부르는 양자 물리학 용어입니다. 큐비트가 GHZ 상태에 있으면 0과 1만으로는 상태를 나타낼 수 없습니다. 그래서 다음과 같이 수학적으로 표기합니다:

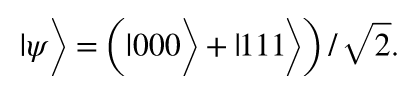
수학에 대해 너무 깊이 들어가지는 않겠지만 (자세한 것을 알고 싶으면 맨 밑에 있는 보너스 자료를 확인해주세요.) 튜토리얼에서 알 수 있듯이, 중첩 상태에 있는 한 개의 큐비트를 이렇게 나타낼 수 있습니다:

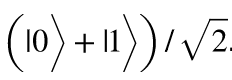
Controlled-Not (CNOT) 게이트를 이용해서 이 큐비트를 다른 두 개와 결합하면 GHZ 상태(상태가 하나의 0이나 하나의 1로 표현된게 아니라 세개의 0 (000)과 세개의 1(111)로 표현 된 것을 주목하세요)를 얻을 수 있습니다.

이 이상한 |〉 기호는 무엇일까요?

브라-켓 표기법은 양자컴퓨팅에서 큐빗을 나타내기 위해 매우 흔하게 쓰입니다. (클래식 비트나 일반적인 숫자와는 상반됩니다) 이 맥락에서 |0〉는 0 상태의 큐비트를 나타내고, |1〉은 1 상태의 큐비트를 나타냅니다.

튜토리얼에서 볼 수 있듯이, 마찬가지로 이 브라켓 표기법으로 여러 큐비트들을 나타낼 수 있습니다. 특히 이 표기법은 큐비트 상태를 벡터로 나타내기 위해 사용됩니다. 깊게 들어가진 않겠지만 만약 여러분이 양자컴퓨팅을 더 다루고 싶다면, 만약 아래쪽에 있는 보너스 자료 링크의 내용을 더 자세히 알고싶다면 양자 상태 벡터를 필수적으로 이해해야 합니다.

벨(Bell) 상태란 무엇일까요?
GHZ 상태가 3개의 얽힌 큐비트를 나타내듯이, Bell 상태는 2개의 얽힌 큐비트를 나타냅니다. 이 튜토리얼에서 회로를 만들 때 먼저 Bell 상태를 생성하여 처음 2개의 큐비트를 연결하고 그 다음에 첫번째 큐비트와 3번째의 큐비트를 연결하여 GHZ 상태를 생성합니다.

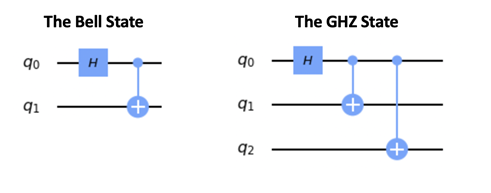
Tutorial Part 2 — 회로 시각화

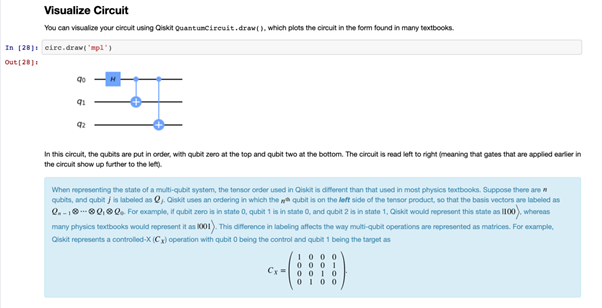
짠! 회로를 빌드하고 시각화했습니다!

참고: circ.draw('mpl') 대신 circ.draw()를 실행했다면, (앞에서 언급된 것과 유사한) 회로의 덜 예쁜 시각화를 얻을 것입니다.

파란 상자의 정보는 양자 컴퓨팅 이론으로 뛰어들기 시작합니다. 튜토리얼을 완료하기 위해서는 이 내용을 완전히 이해할 필요는 없습니다만 이 튜토리얼 이후에 양자 여행을 이어나가는 것에 관심 있다면 텐서곱(Tensor Product, 동그라미 안에 X표시가 된 연산자)과 큐비트의 행렬 표현에 대해 배우는 것으로 시작하길 추천 드립니다(마지막에 있는 보너스 자료의 링크를 확인하세요).

Tutorial Part 3 — 백엔드로 상태벡터 계산하기

이제 이번 파트에서 실제로 회로를 작동시키고 결과를 얻어 봅시다.

튜토리얼에서 실제 양자컴퓨터에서 회로를 실행하는 방법을 보여주지는 않지만, 몇 개의 다른 시뮬레이터를 실행합니다. 시뮬레이터는 더 빠르고 노이즈가 없는 완벽한 계산 결과를 보여줍니다. Qiskit은 다양한 양자 시뮬레이터 ‘백엔드(backends)’를 사용하여 동작하고, 각 시뮬레이터는 다른 형식으로 그 결과를 반환합니다. (예: statevector, unitary 와 QASM)

*실제 양자컴퓨터는 ‘소음(‘noisy’)’을 고려하는데, 이는 항상 올바른 결과가 나오지 않기 때문에 여러 번 실험을 해야 정확한 결과를 판단할 수 있다는 것을 의미합니다. 맨 밑에 있는 보너스 자료를 확인해보시면 아시겠지만, 소음 감소(Noise reduction)는 매우 중요한 연구 영역입니다. (연구 영역은 하드웨어와 소프트웨어를 포함합니다)

상태벡터란 정확히 무엇일까요?

3개의 클래식 비트가 있는 경우를 생각해 봅시다. 계산 과정에서 이 비트들은 0 또는 1의 값을을 가질 수 있게되므로 다음과 같이 총 8개의 조합을 만들어 낼 수 있습니다.

하지만, 앞에서 말했다시피 정확히 0과 1의 조합으로 중첩상태를 표현한다는 것은 불가능합니다. 대신에 상태벡터를 이용하여 이를 나타낼 수 있습니다. 상태벡터(State Vectors)는 양자 상태를 나타내는 복소수 벡터(Complex Vector)입니다. 복소는 ‘실수’ 부분과 ‘허수’ 부분을 갖고 있다는 것을 의미합니다.(고등학교 때 기억나시나요?) 3 qubit GHZ 상태를 상태벡터로 나타내면 다음과 같습니다:

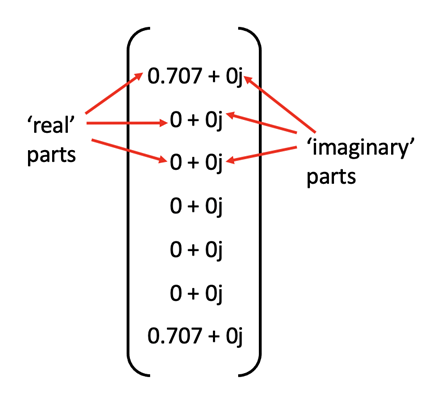
다음의 코드를 사용해서 Qiskit statevector 시뮬레이터로 상태벡터를 계산해 볼 수 있습니다:

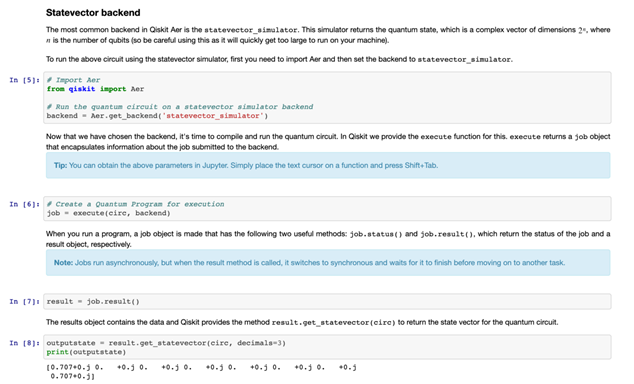
위에 보여진 행렬 표현과 다소 다른 형식이라 당황스러우신가요? 포맷이 다를 뿐 이라고 이해하시면 됩니다.
행렬의 스타일이 여러분의 마음에 들지 않는다면, Qiskit에서 시각화 라이브러리를 통해 다양한 옵션을 선택할 수 있습니다. (튜토리얼 2(https://github.com/Qiskit/qiskit-tutorials/blob/5cf8f3445fd900bb1ec3d5863e294ab355551135/tutorials/circuits/2_plotting_data_in_qiskit.ipynb) 는 가장 일반적인 것 중 일부에 대한 개요를 제공합니다.)

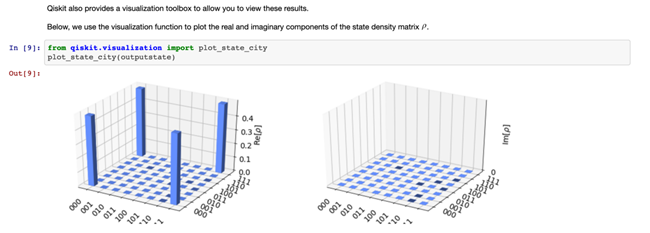
plot_state_city 함수를 사용해서 상태 벡터를 시각화 해보았습니다.

좋습니다. 이것이 가장 직관적인 시각화가 아닐 수 있지만, 왼쪽에 있는 그래프는 statevector의 ‘실수’ 부분을 나타내고, 오른쪽 그래프는 ‘허수’부분을 나타냅니다. 파란색 막대기의 높이는 우리가 관측할 때 큐비트가 0과 1의 조합으로 붕괴될 확률을 나타냅니다. 이 경우 큐비트가 000이나 111로 붕괴될 확률은 대략 50 대 50이며, 절대 다른 조합으로는 붕괴되지 않을 것입니다. (회로 게이트의 설치 방법 때문에)

이런 부분이 양자컴퓨팅의 놀라운 부분입니다. 게이트의 특정한 조합을 선택하여, 큐비트를 잘 처리하여 모든 가능한 경우의 수(8개)가 아닌 단 2개의 결과만을 계산해 낼 수 있습니다. 양자 알고리즘을 개발한다는 것의 아주 기본적인 부분이라고 볼 수 있습니다.

Tutorial Part 4 — 백엔드로 유니터리 계산하기 (Unitary Backend)

유니터리(Unitary)란 무엇인가요?

여기서 유니터리(unitary)라고 할 때 그것은 큐비트 게이트가 유니터리 행렬로 표현될 수 있음을 의미합니다. 행렬은 '켤레전치 또한 가역'일 때 유니터리입니다(이것이 잘 이해되지 않는다면 비디오(https://www.youtube.com/watch?v=DUuTx2nbizM) 를 시청하기 바랍니다).

양자 물리학에서 이 개념은 종종 다음과 같이 표현됩니다:

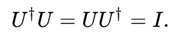
U가 원본 행렬일 때, U†는 컬레전치를, I는 단위행렬을 의미합니다(이런 표기법은 물리학 교재에서 많이 보게 될 겁니다).

따라서, Qiskit의 유니터리 시뮬레이터는 우리가 작성한 회로의 결과를 8x8 유니터리 행렬로 보여줄 것입니다. 이 결과 또한 주피터 노트북에서는 그다지 보기 좋은 형태가 아니지만, 기본적으로 그것은 다음과 같습니다:

Tutorial Part 5 — OpenQASM Backend

거의 다 끝나갑니다! 뇌가 녹지 않고 여기까지 온 것은 대단합니다.👏👏👏
이 마지막 섹션에서는 회로 출력을 여러 번 시뮬레이션 해보세요. (실행 횟수가 많을 수록 결과가 더 정확해 집니다.)

|0〉, |1〉의 계산 기저(basis : 선형독립적인 벡터)란 무엇일까요?
이 용어는 큐비트가 측정되는 방식을 말합니다. 이 튜토리얼의 목적상 여러분이 알아야 할 것은 우리의 큐비트가 클래식 비트로 붕괴될 때 큐비트는 0 또는 1의 값을 갖는다는 것입니다. 사용할 수 있는 다양한 기저가 있지만, |0〉, |1〉 기저( Z 기저(주석: Z축으로 측정이 진행되기 때문))가 가장 흔합니다.

이 방정식은 무엇을 의미하나요?

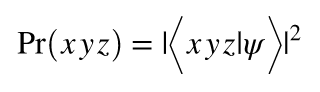
이 방정식은 Born Rule이라고 하며 회로를 실행할 때 0과 1의 특정 조합(예를들어 000 010 100 등등)을 얻을 확률을 대수적으로 계산하는데 사용됩니다. GHZ 상태의 경우 이 방정식은 결과가 000과 111이 나올 확률이 1/2이고, 다른 경우는 0이라는 것을 알려줍니다. 그런 다음 회로를 여러 번 실행하고 000과 111이 몇 번 나오는지 확인하여 이 확률을 검증할 수 있습니다. 이 튜토리얼에서 코드를 이해하기 위해 이 공식의 수학적 증명을 알필요는 없습니다만, 만약에 Born Rule과 다른 양자역학 원리에 대해 자세히 알고 싶다면 보너스 자료를 확인해주세요.

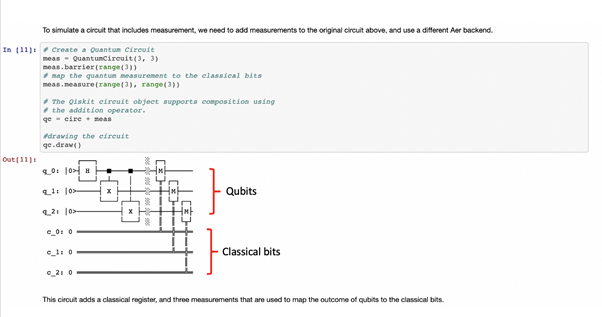
위 섹션은 비교적 명백합니다. 한 가지 주목할 점은 아래에 보이는 새로운 라인은 3개의 “클래식” 비트를 나타냅니다. 이 클래식 비트는 측정(측정된 큐비트 당 1개의 클래식 비트)을 통해 얻은 정보를 저장하는 데 사용됩니다. 일부 회로 다이어그램에서는 공간을 줄이기 위해 이러한 클래식 비트 라인 여러 개를 하나의 줄로 합쳐서 표현하기도 합니다.

다음 단계에서 회로를 여러번 실행하고 (정확하게는 1024번) 그 결과를 집계하는 작업을 합니다. 이론적으로 ‘완벽한’ 양자컴퓨터 (즉, 시뮬레이터)에서는 000과 111만 결과로 나오겠지만, 실제 양자컴퓨터에서 회로를 실행하면 실제 장비의 소음때문에 몇 가지 변칙적인 결과가 나올 수 있습니다.

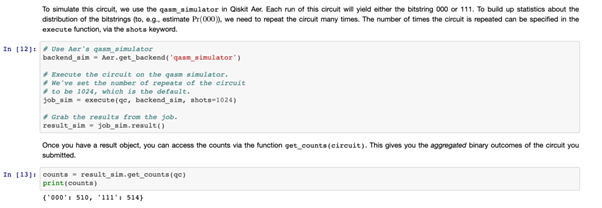
시뮬레이터에서 회로가 실행된 1024번 중 ‘000’이 나온 측정 결과가 510번 ‘111’이 나온 측정 결과가 514번이라는 것을 get_counts 함수를 사용하여 알 수 있습니다. 시뮬레이터를 사용한 결과이기 때문에 다른 결과는 없었습니다.

마지막으로 이 결과를 히스토그램으로 시각화해보겠습니다:

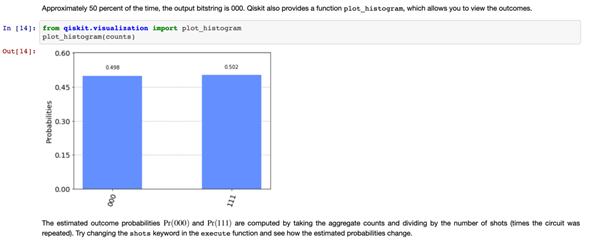
🎉🎉🎉 축하합니다 해내셨군요!🎉🎉🎉
여기 제가 약속했던 보너스 자료가 있습니다:
● Qiskit 튜토리얼 나머지 부분: https://github.com/Qiskit/qiskit-tutorials/blob/master/start_here.ipynb
● 컴퓨터 사이언스 너드를 위한: https://www.youtube.com/watch?v=F_Riqjdh2oM&t=4413s
● 역사 너드를 위한: https://www.youtube.com/watch?v=iol5936dZho&list=PLhyKYa0YJ_5ATEDqJRuoIvOH-eVkHP7ms
● 큐비트를 나타내는 다양한 방법을 빠르게 요약한 비디오: https://www.youtube.com/watch?v=tBnWG_95F9c
● 대수학과 브라켓 표기법: https://arxiv.org/pdf/1803.07098.pdf
● 양자컴퓨터에서의 ‘소음’: https://www.youtube.com/watch?v=AUAkoEiutOE
● 일반적인 양자 용어와 개념 사전 : https://www.quantiki.org/
● 양자역학을 학습하기 위한 자료: https://lookingglassuniver.wixsite.com/blog/post/how-to-learn-quantum-mechanics-on-your-own

소감

제대로 번역 작업을 해보는 것은 이번이 처음이었는데, 공부도 되고 재미있었습니다. 뜻을 이해하는 것은 쉬워도 우리말로 이해하기 쉽게 쓰는 것은 어려운 것 같습니다. :>