Graph

흔히 그래프라고하면 우리는 이런 그래프를 생각한다.

그런데 컴퓨터공학(자료구조)에서의 graph는 전혀 다른 모습이다.

이런식으로 네트워크 망같은 모습을 하고 있다.

A, B, C, D, E 각각의 점들이 서로 복잡하게 연결되있는 관계를 표현한 자료구조를 graph라고 한다.
A와 B처럼 직접적인 관계를 가지고 있는 선이 있고, B와 D처럼 간접적인 관계를 가지고 있는 선도 있다.
각각의 원들(A, B, C...)은 정점(vertex)이라고 불리고, 각 정점을 연결하는 선들을 간선(edge)라고 부른다.

실생활에서 우리가 그래프 자료구조를 이용하는것중에 대표적으로 네비게이션(길찾기)이 있다.
서울에서 부산까지 가는중에 대전에 들린다 하면 서울, 대전, 부산은 정점으로 사이사이 선들은 간선으로 볼 수 있다.

서울 부산 대전이 서로 이어져있는건 알 수 있지만, 서로간에 거리에 대해서는 알 수 없다.
간선이란건 그저 이어져있다는 정보만 주기때문에 이런 그래프들을 비가중치 그래프라고 부른다.

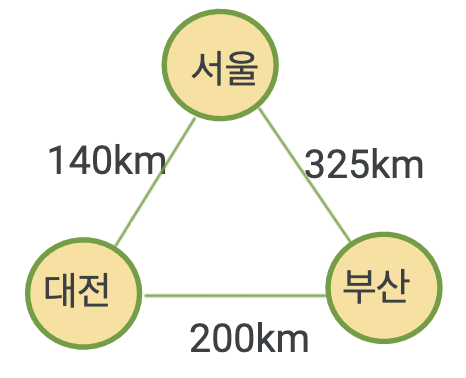
이런식으로 정보가 추가되어야 가중치 그래프라고 불릴수 있다.
더욱 더 자세한 정보들을 담고, 정점과 간선도 확장해 나가면 네비게이션에 쓰는 자료구조와 비슷해지는 거라고 볼 수 있다!

그래프의 표현방식(인접행렬, 인접 리스트)

인접행렬

두 정점간에 간선이 직접 이어져있을때 이 두 정점은 인접한 정점이라고 본다.

인접행렬로 한번 표현해보겠다.

위와같이 표현이 가능하다.
인접행렬은 주로 두 정점 사이에 관계가 있는지, 없는지를 확인하거나 가장빠른경로를 찾고자 할 때 사용된다.

인접 리스트

인접 리스트는 각각의 정점이 어떤 정점과 인접하고 있는지 리스트의 형태로 볼 수 있는 방식이다.
위 그래프를 인접 리스트형식으로 만들어보자.

인접 리스트는 메모리를 효율적으로 사용하고 싶을때 인접행렬 대신 사용한다.
왜냐하면 인접행렬은 연결 가능한 모든 수를 저장하기 때문이다.!