🔗 함수적 종속 (FD, Functional Dependencies)
어떤 테이블 R에서 속성 X의 각 값에 대해 속성 Y의 값이 오직 하나만 연관되어 있을 때, Y는 X에 함수적 종속이라고 하고 R.X → R.Y로 표현한다.
이때 R.X를 결정자(determinant), R.Y를 종속자(dependent)라고 한다.
🔍 예시
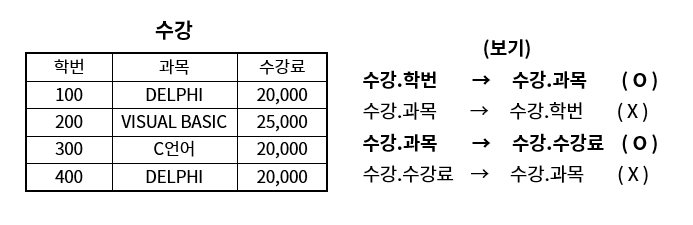
학번에 대해 과목의 값이 오직 하나만 연결되어 있다.
과목에 대해 수강료의 값이 오직 하나만 연결되어 있다.
🔑 키에 따른 함수적 종속
아래의 학생 테이블에서 함수적 종속이 있는지 알아봅시다.
1. {학번} → {이름} O
2. {이름} → {학번} X
3. {학번} → {학번} 뜻이 없는 함수적 종속
4. {학번, 이름} → {이름} 뜻이 없는 함수적 종속
결정자에 기본키, 후보키, 슈퍼키가 오면 키의 특성 중 유일성을 만족하기 때문에 무조건 함수적 종속이 성립한다.
❗ 인스턴스만 보고 결정할 수 없다
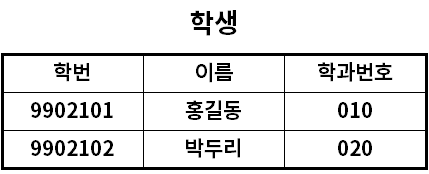
위 인스턴스가 {이름} → {학번}을 어기지는 않지만, 함수적 종속이 있다고 결론지을 수 없다.
함수적 종속은 데이터베이스 설계자가 데이터베이스를 설계할 때, 각 스키마에서 지켜져야 할 함수적 종속을 결정한다.
🤷🏻♀️ 뜻이 없는 함수적 종속 (trivial FD)
- β ⊆ α 일때 , α → β (부분 집합)
- 왼쪽 속성의 집합과 오른쪽 속성의 집합이 같을 때
👯♂️ 함수적 종속 집합의 클로저 (closure)
함수적 종속 집합 SFD (a set of FDs)가 있을 때, SFD의 클로저 SFD+는 SFD에 묵시적으로 포함되어 있는 모든 함수적 종속까지도 포함하는 집합을 가르킨다.
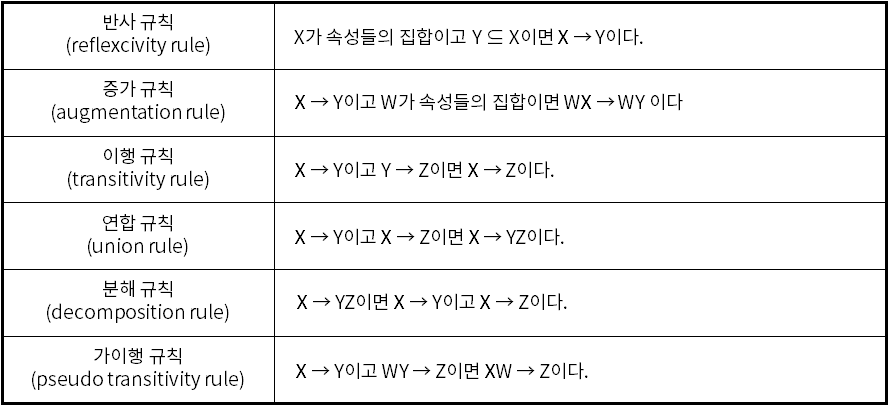
🤙🏻 암스트롱(Armstrong) 규칙
- 그리스 글자
(α, β, ...)는 각각 속성의 집합을 나타낸다. αβ는α∪β이다 (합집합)- 영어 대문자
A는 속성 A만으로 이루어진 속성의 집합 A를 나타낸다. - 영어 대문자 두 개를 붙인
AB는 속성 A와 B로 이루어진 속성의 집합 A, B를 나타낸다.
1. 반사 규칙 (reflexivity rule)
β ⊆ α일 때, 함수적 종속α → β가 있다.{이름} ⊆ {학번, 이름}일 때 함수적 종속{학번, 이름} → {이름}- 뜻이 없는 함수적 종속(trivial FD)을 이끌어내는 규칙.
2. 증가 규칙 (augmentation rule)
α → β가 있을 때, 왼쪽과 오른쪽에 속성의 집합r를 모두 더한 함수적 종속αr → βr도 존재한다.{학번} → {이름}이 있을 때,{학번, 전화번호} → {이름, 전화번호}도 존재한다.
3. 이행 규칙 (transitivity rule)
α → β와β → r가 있을 때, 함수적 종속α → r가 존재한다.{학번} → {학과번호}와{학과번호} → {학과이름}이 있다면,{학번} → {학과이름}도 존재한다.
4. 연합 규칙 (union rule)
- 함수적 종속
α → β와α → r가 있을 때, 함수적 종속α → βr도 존재한다. {학번} → {이름}과{학번} → {학과번호}가 있을 때,{학번} → {이름, 학과번호}도 존재한다.
5. 분해 규칙 (decomposition rule)
- 함수적 종속
α → βr가 있으면,함수적 종속α → β와α → r도 존재한다. {학번} → {이름, 학과번호}가 있을 때,{학번} → {이름}과{학번} → {학과번호}도 존재한다.
6. 가이행 규칙 (pseudotransivity rule)
- 함수적 종속
α → β와βr → δ가 있을 때, 함수적 종속αr → δ도 존재한다. {주번} → {학번}과{학번, 과목번호} → {성적등급}이 있으면,{주번, 과목번호} → {성적등급}도 있다.
정리