Tree

Red-Black Tree에 앞서 Tree의 정의와 용어에 대해 먼저 정리해 봅시다.
트리란 루트를 중심으로 노드들이 비순환적 경로로 연결되어 있는 그래프를 말합니다.

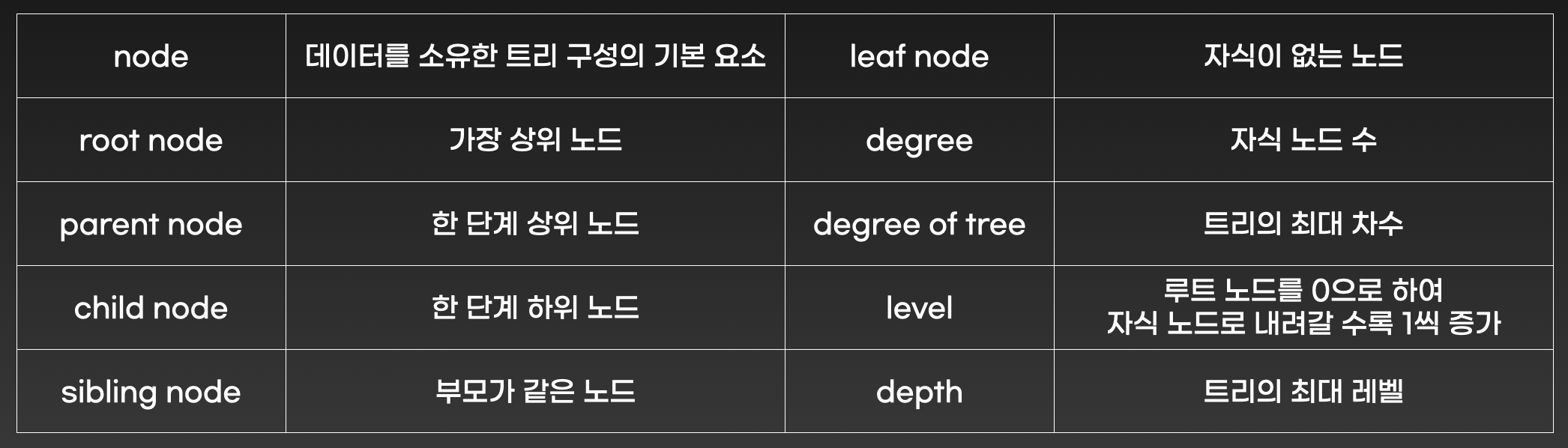
위 트리 용어를 그림으로 나타내면 아래 사진과 같습니다.

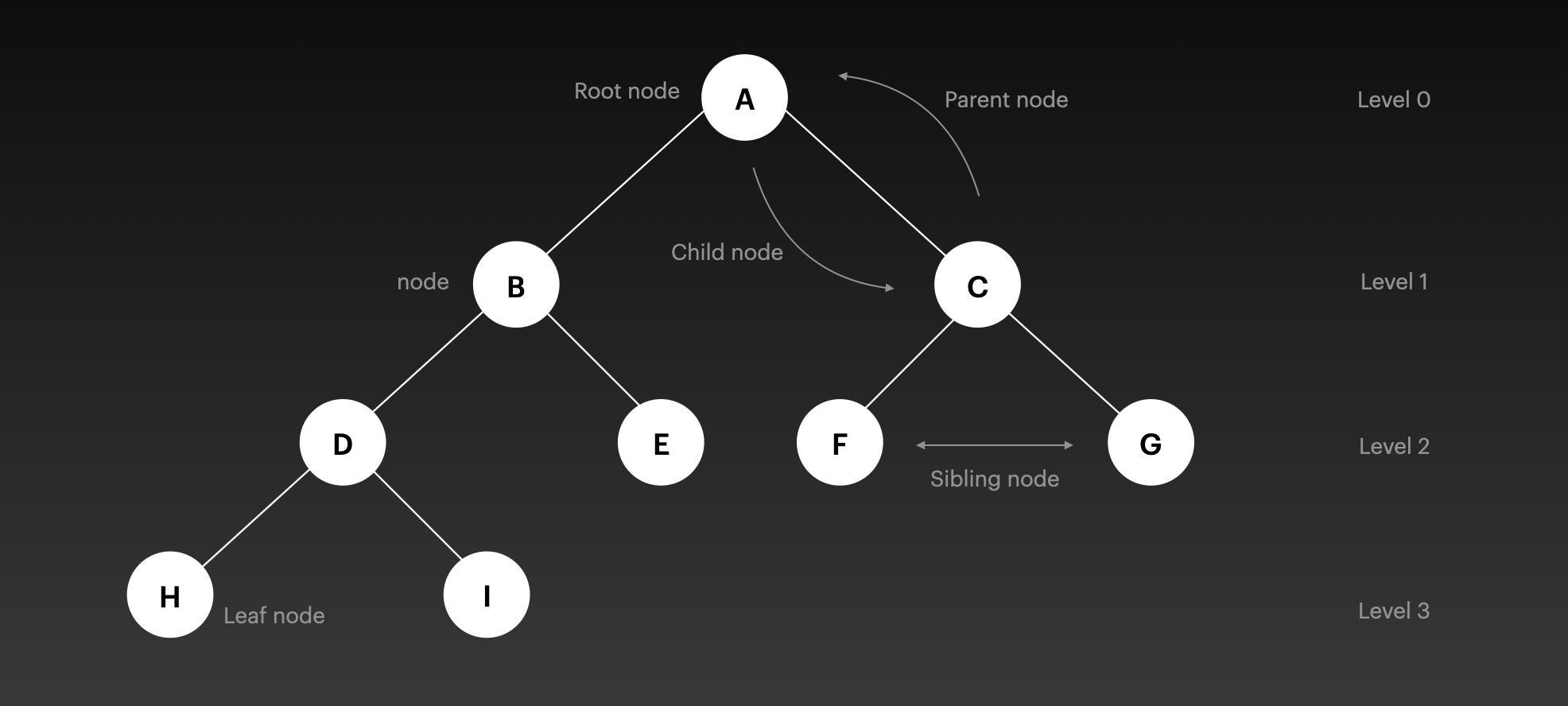
Binary Tree

Binary Tree이진 트리는 최대 두 개의 자식 노드를 가지는 트리입니다.

종류

Full binary tree 정이진트리
모든 노드가 0개 또는 2개의 자식 노드를 가지는 트리

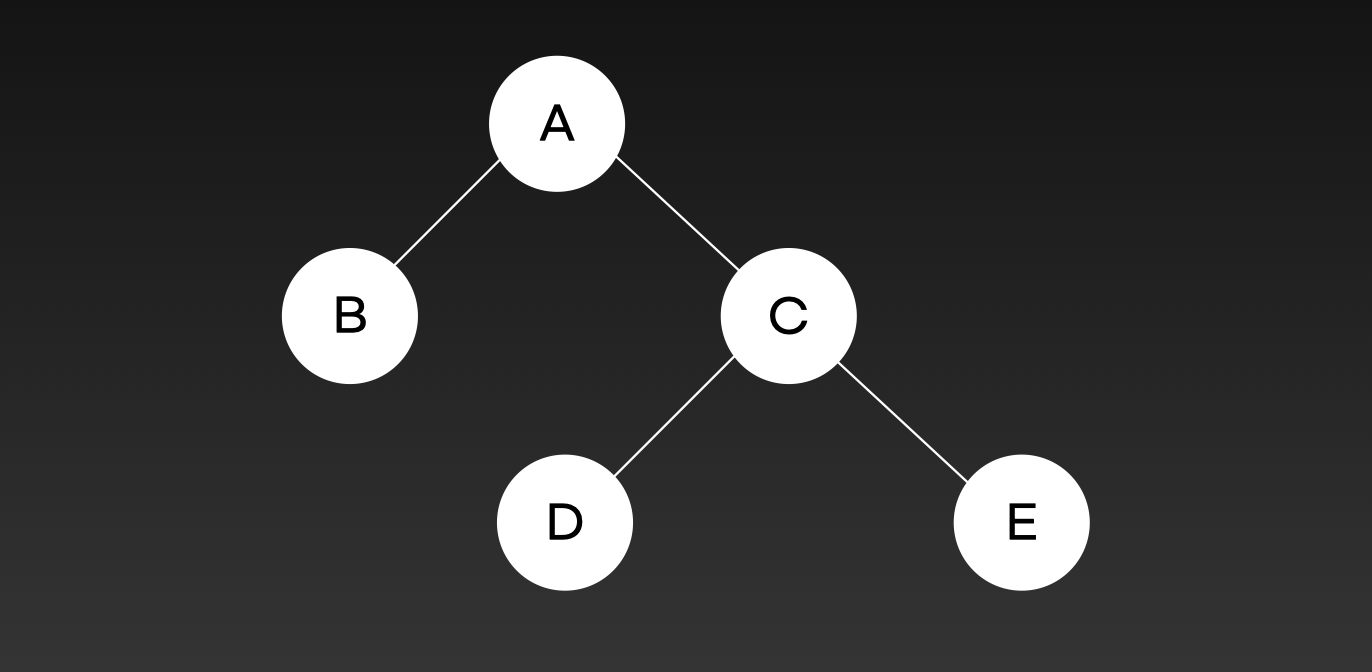
Complete binary tree 완전 이진 트리
마지막 level을 제외한 모든 노드가 채워져 있고,
마지막 level은 왼쪽부터 채워져 있는 트리

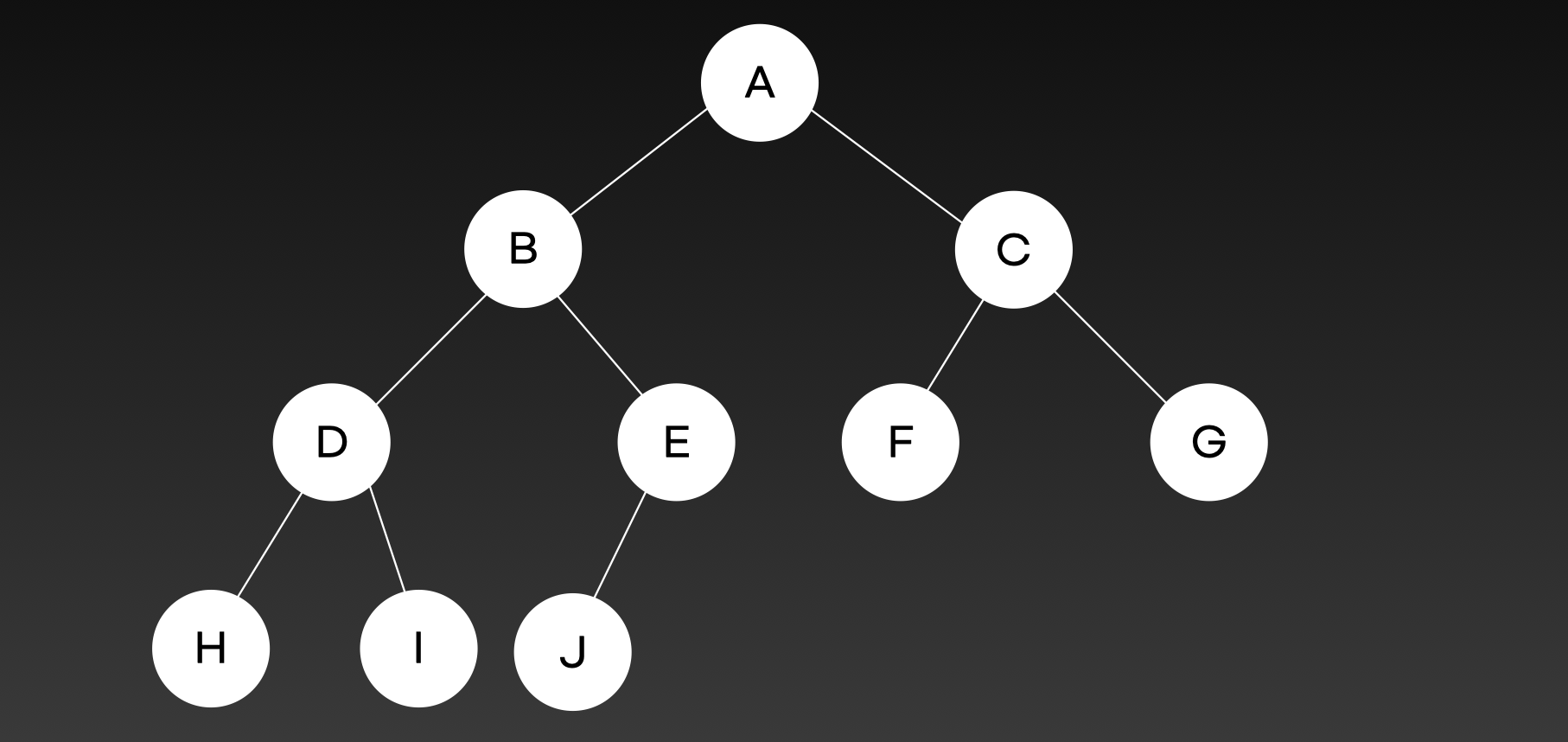
Perfect binary tree 포화 이진 트리
모든 내부 노드 (internal node) 가 두 개의 자식 노드를 가지고,
모든 leaf node가 동일한 level을 가지는 트리

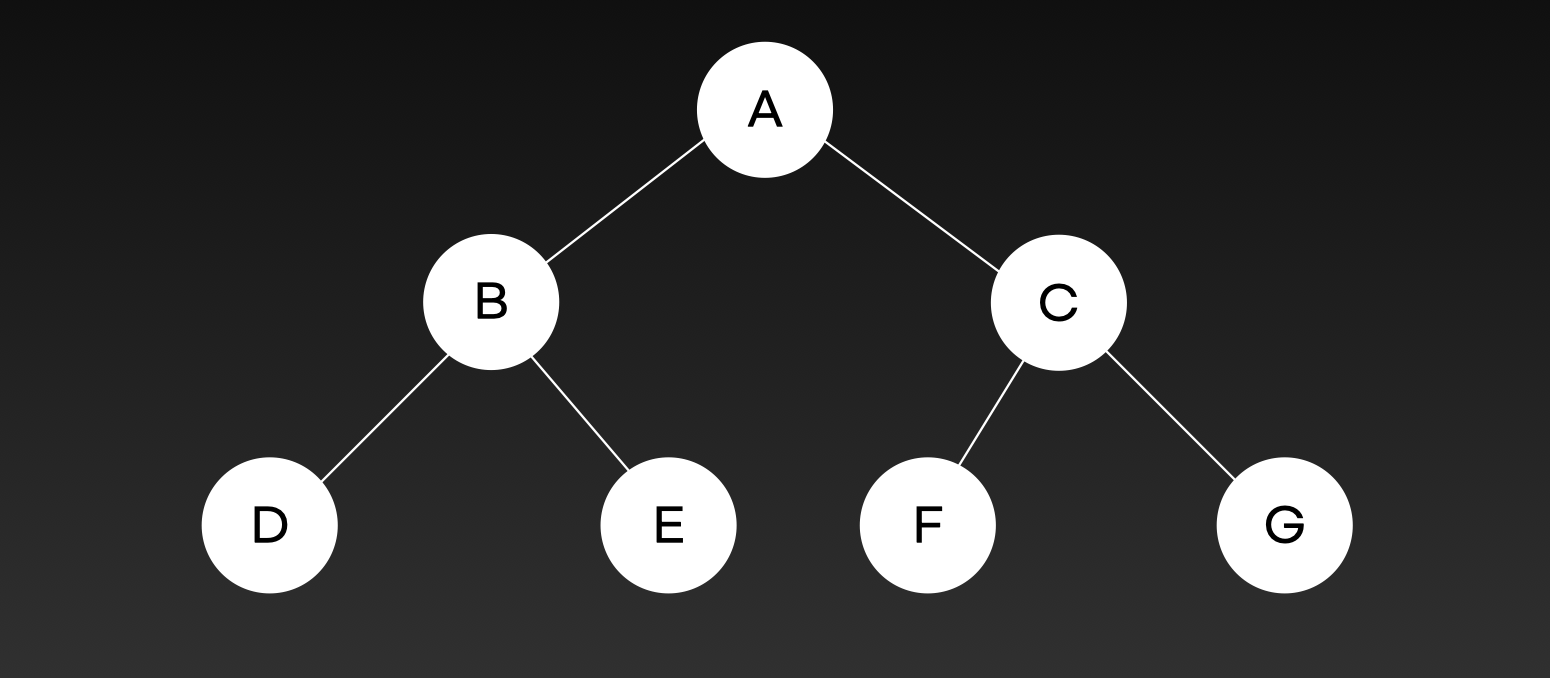
Balanced binary tree 균형 이진 트리
모든 leaf node의 깊이 차이가 최대 1인 트리

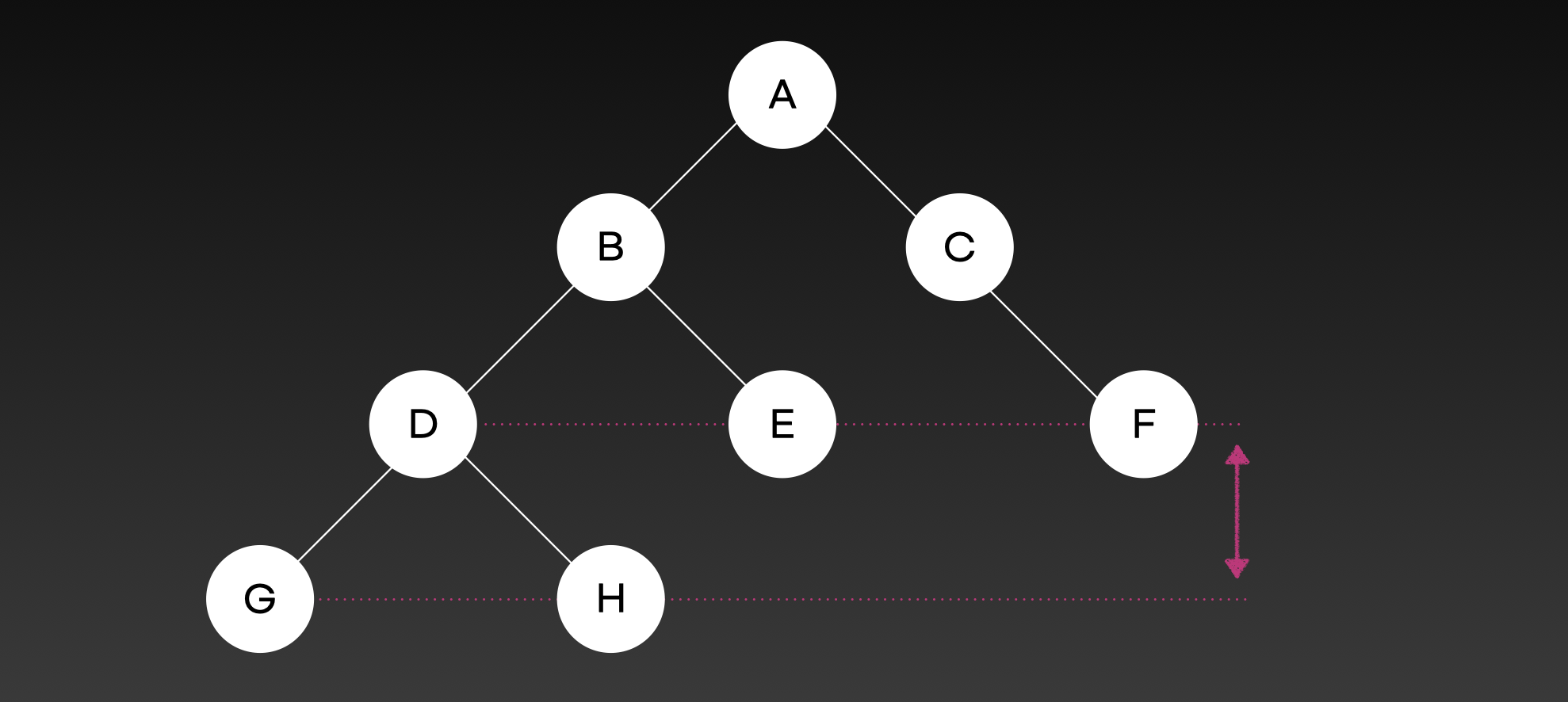
Skewed binary tree 사향 이진 트리
모든 노드가 좌/우 한 쪽으로만 치우친 트리

Binary Search Tree (BST)

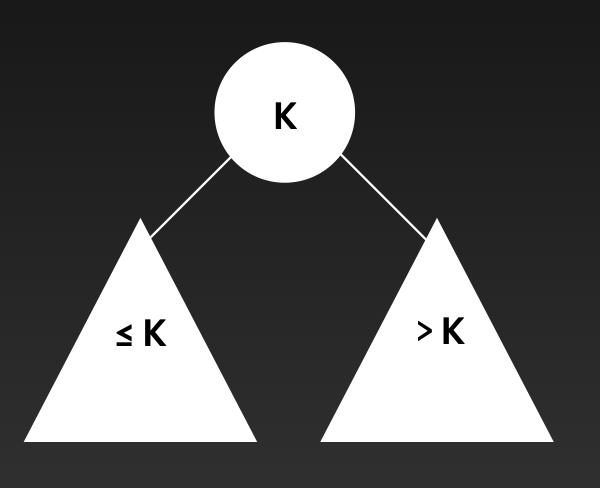
Binary Search Tree 이진 탐색 트리는 다음과 같은 속성을 가진 이진 트리입니다.

• 노드의 왼쪽 서브트리는 노드의 키보다 작거나 같다.
• 노드의 오른쪽 서브트리는 노드의 키보다 크다.

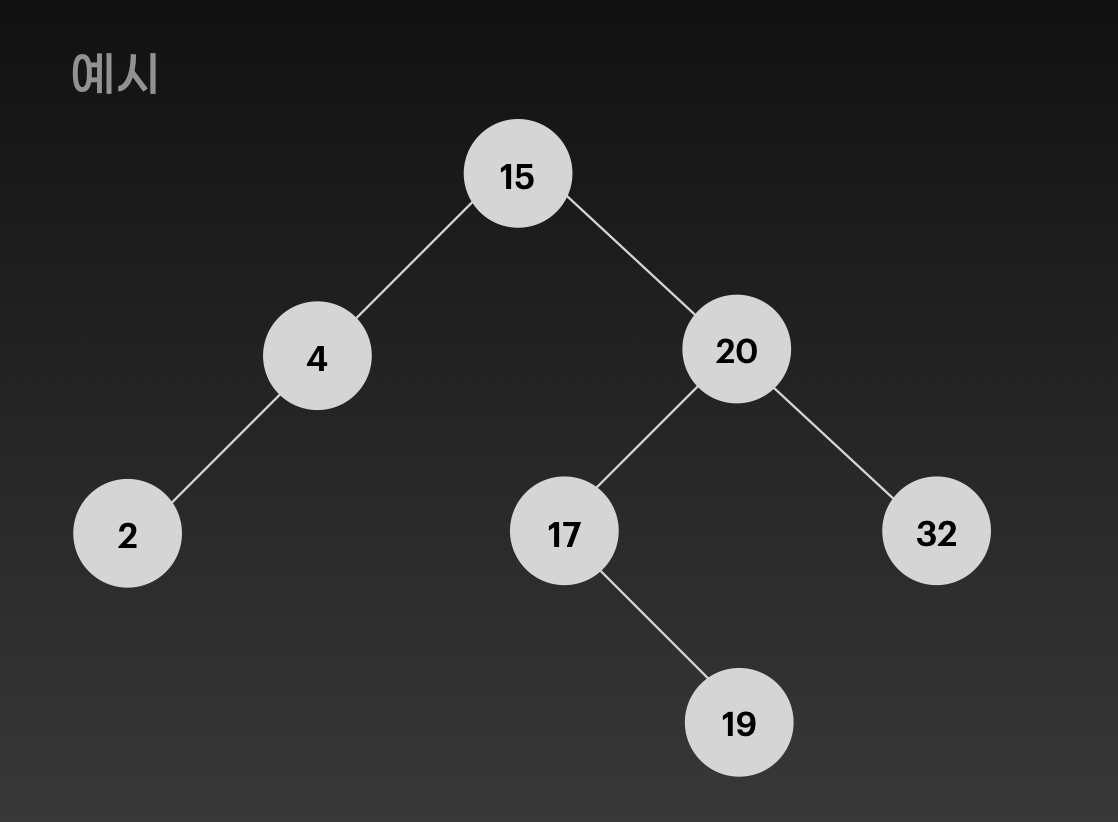
BST는 Search에 소요되는 시간복잡도는 트리의 높이가 h일 때, O(h)입니다.

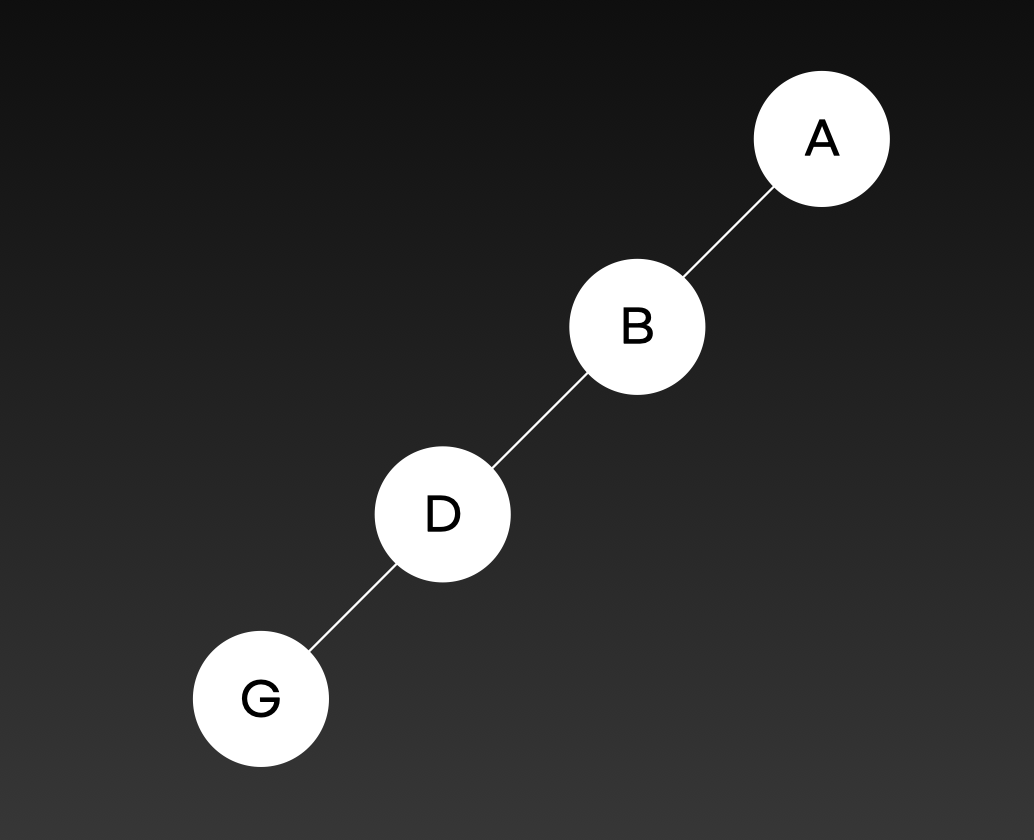
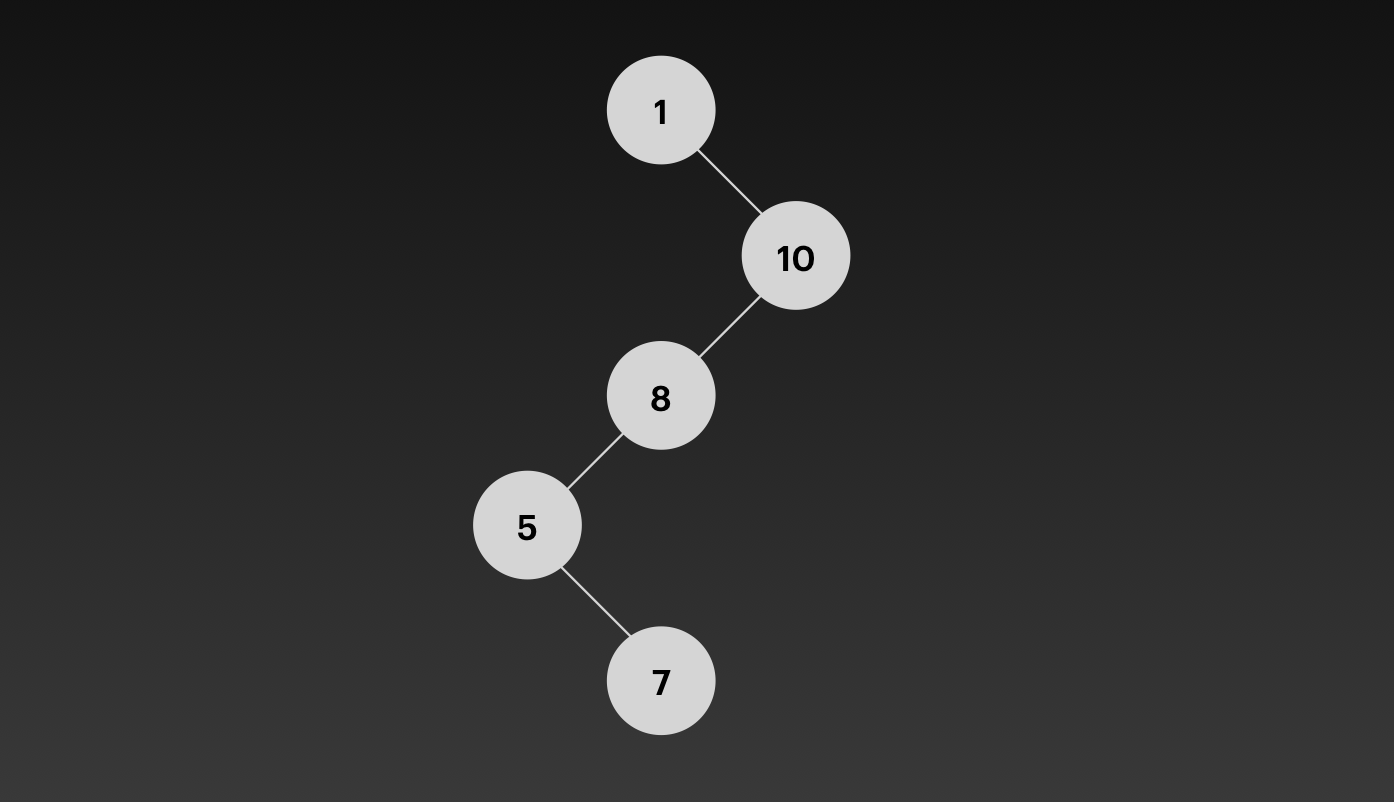
최악의 경우 h는 n-1입니다.
이는 아래 사진과 같이 연결리스트처럼 leaf node를 제외한 모든 노드가 자식을 하나씩만 가질 경우를 말합니다.

Balanced BST

Balanced BST 균형 이진 탐색 트리란 시간복잡도 O(log n)을 유지하는 이진 탐색 트리를 말합니다.
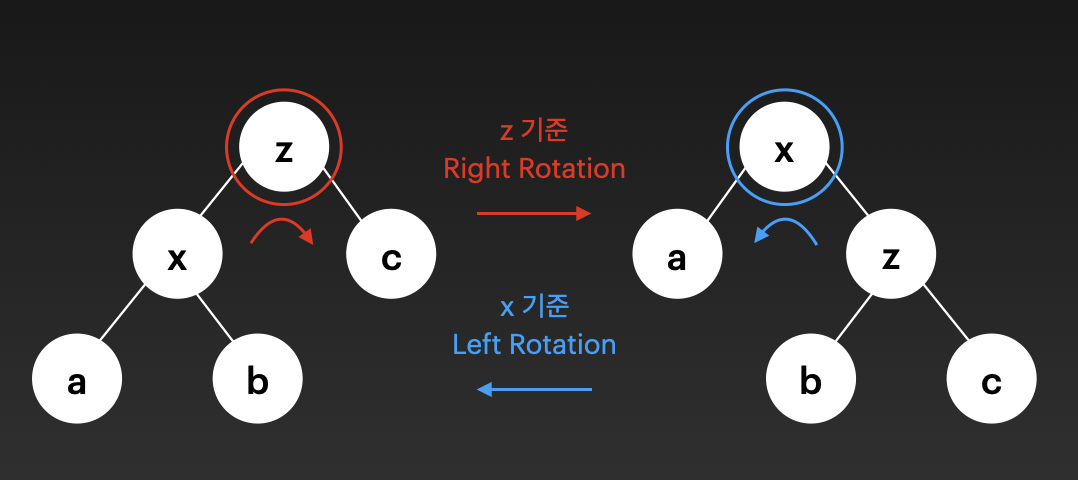
O(log n)을 유지하기 위한 조정 연산은 회전이다.

Red-Black Tree

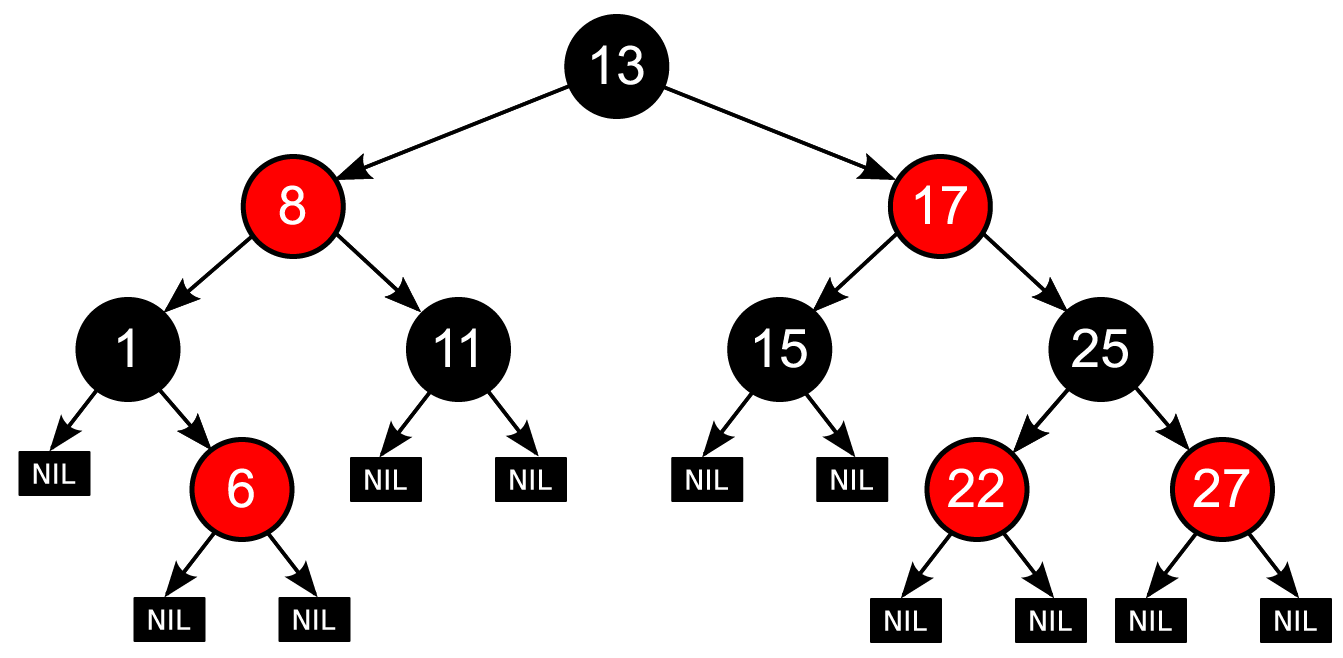
Red-Black Tree 레드-블랙 트리는 앞서 이야기 한 Balanced BST 중 하나로, 다음과 같은 속성들을 갖습니다.
1. 모든 노드는 Red나 Black이어야 한다.
2. Root 노드는 Black이다.
3. leaf(NIL) 노드는 Black이다.
4. Red 노드의 자식 노드는 Black이다.
5. 각 노드에서 leaf node로 갈 때의 Black 노드 수는 항상 같아야 한다.

Insert (삽입 연산)

삽입하는 노드를 Z라고 했을 때,

• red 색상인 Z를 삽입합니다.
• 위반 사항을 고치기 위해 최대 2번의 회전과 색 조정을 거칩니다.

why red?

• root와 NIL 노드가 black이어야 한다는 것(②, ③)과
• red 노드의 자식 노드는 black이어야 한다는 것(④)

위 두 가지 속성을 깨뜨릴 수는 있지만 수정하기 쉽기 때문입니다.

1. Z가 root일 때

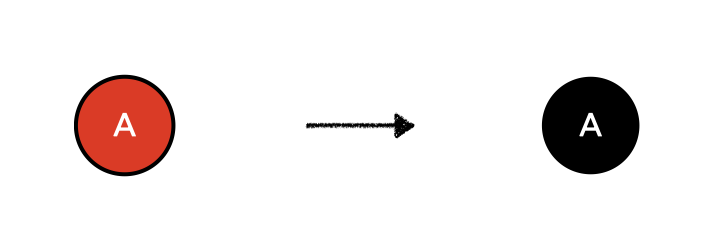
Z를 black으로 색을 조정한다.

2. Z.uncle이 red일 때

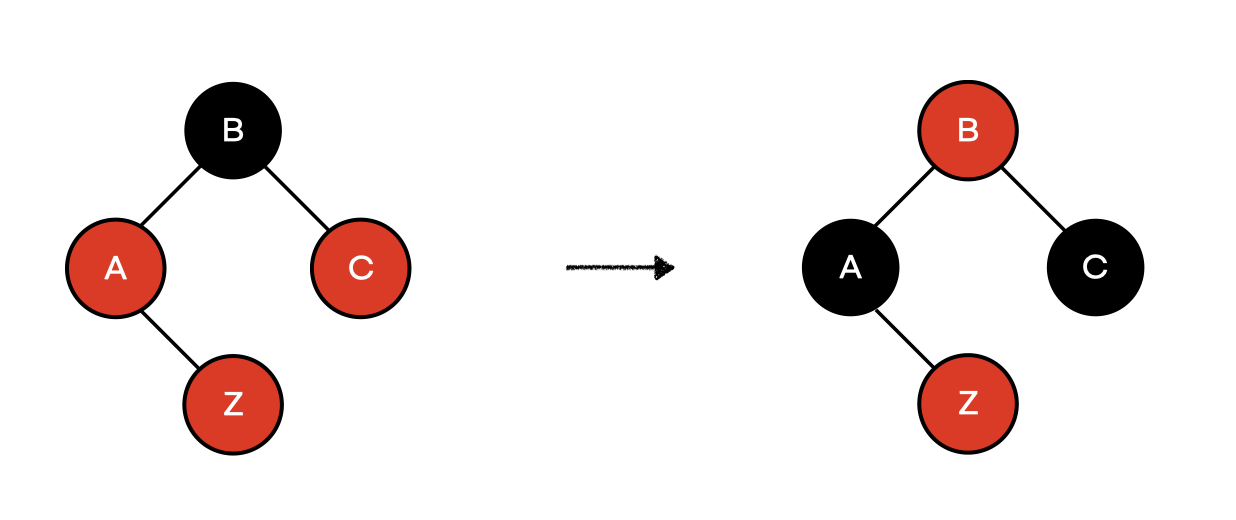
parent(A), uncle(C)을 black으로
grandparent(B)를 red로 색을 조정한다.

위 그림의 트리는 서브트리로 B는 root가 아니다.

3. Z.uncle이 black일 때 (triangle)

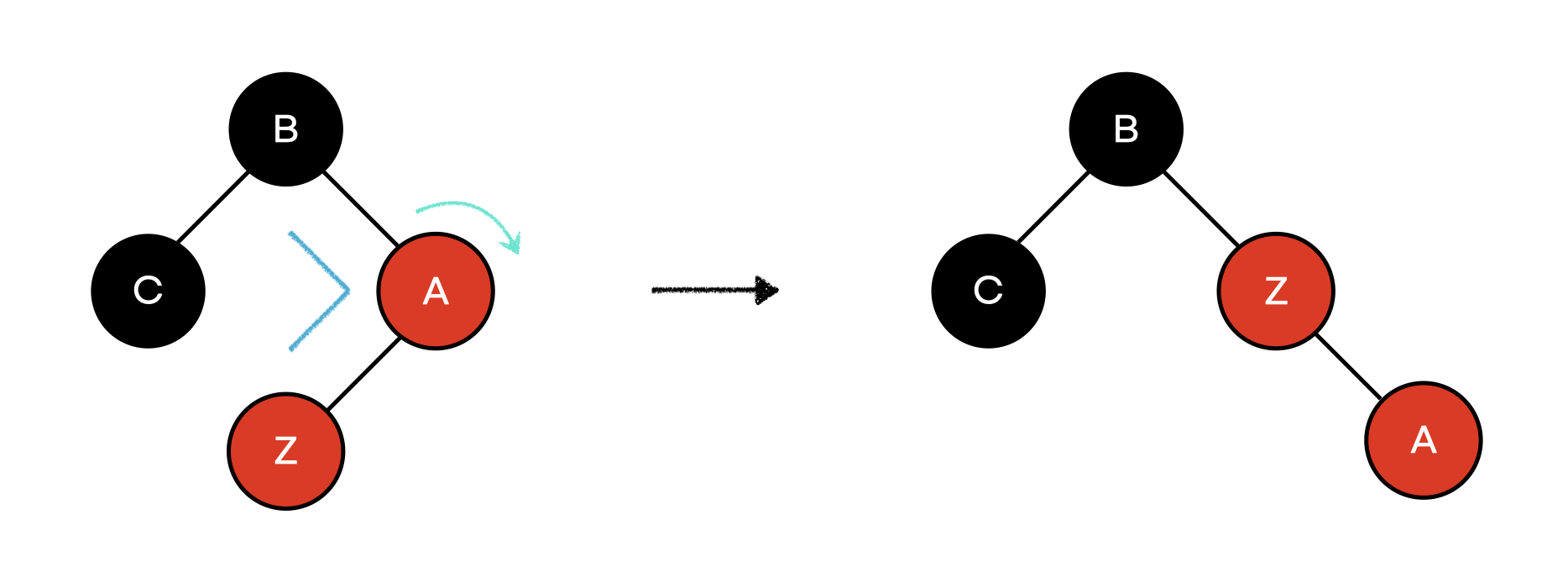
parent(A)를 회전한다.
4. Z.uncle이 black일 때 (line)의 경우가 된다.

4. Z.uncle이 black일 때 (line)

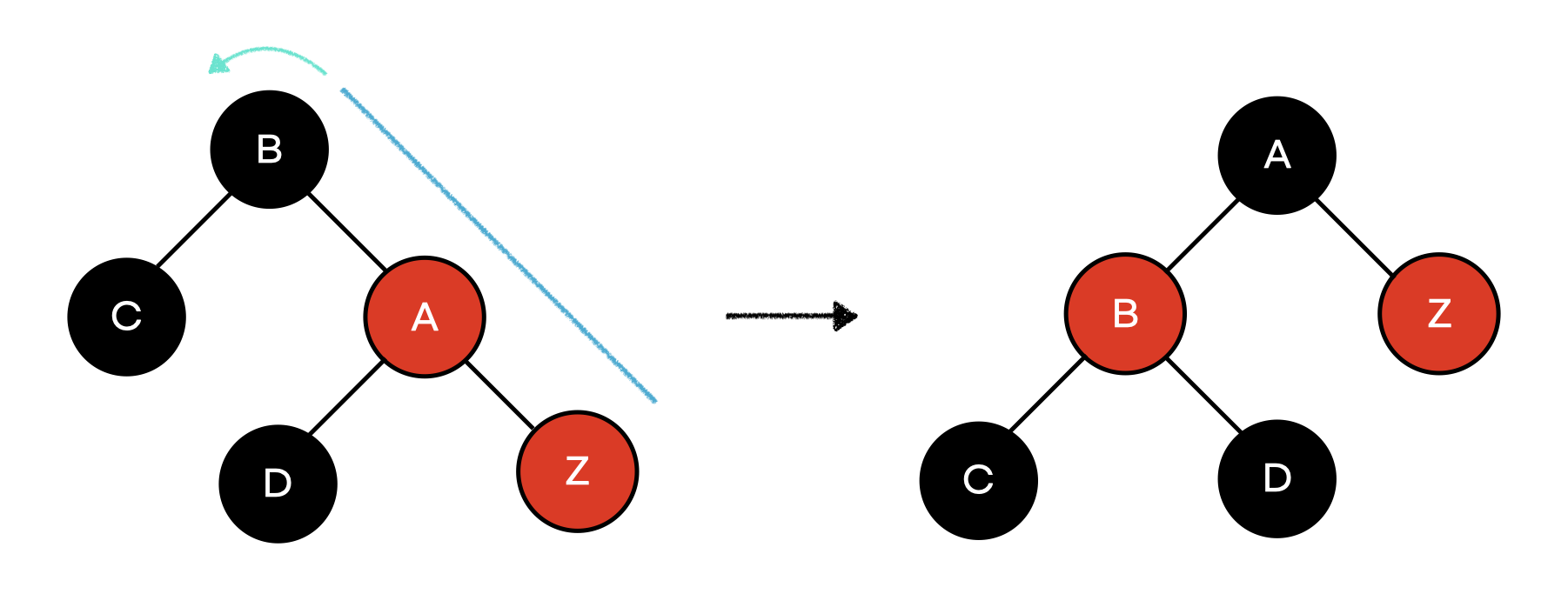
grantparent(B)를 회전하고 색을 조정한다.
위 예시에서는 A를 black으로, B를 red로 조정

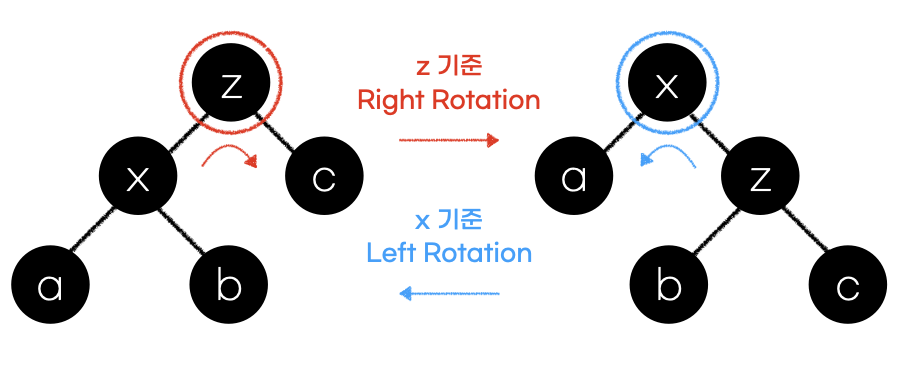
Rotation

삽입 혹은 삭제에서 레드-블랙 트리의 속성을 위반했을 때 수행하는 연산이다.
시간 복잡도는 O(1)이다.

def rotateRight(self, z):
    if not z: 
        return
    x = z.left
    if x == None: 
        return
    b = x.right
    x.parent = z.parent
    if z.parent:    # z가 root면 None일 수 있음
        if z.parent.left == z:
            z.parent.left = x
        else:
            z.parent.right = x
    x.right = z
    z.parent = x
    z.left = b
    if b:
        b.parent = z
    if self.root == z:  # root였다면 정보 업데이트
        self.root = x

참고 자료
Tree (data structure)
자료구조 - 균형이진탐색트리 - 정의와 회전
자료구조 - 균형탐색이진트리 - Red-Black 트리
자료구조 - 균형이진탐색트리 - Red-Black 트리 삽입연산
Red-black trees in 5 minutes — Insertions (strategy)
Red-black trees in 5 minutes — Insertions (examples)