[LeetCode] 530. Minimum Absolute Difference in BST

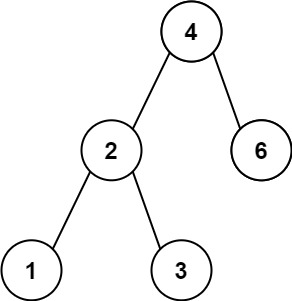
https://leetcode.com/problems/minimum-absolute-difference-in-bst

개요

1. 이진 검색 트리의 root 노드가 주어진다.
   • 노드의 개수는 최소 두개
2. 두 노드 간의 최소 차이를 구해라.

문제 해결 아이디어

• 이진 검색 트리는 각 부모 노드로부터 왼쪽에 위치한 자식 노드는 부모 노드의 값보다 작고, 오른쪽에 위치한 자식 노드는 부모 노드의 값보다 크다
  ➡️ (가정) 자식 노드와 그 상위 노드와 연산을 하면 최소값이다.
  • 리프 노드와 루트 노드가 최소 차이를 갖게 관계식을 만들어보자
  • 리프 노드 x는 x의 부모 노드, 조부모 노드와 최소값의 차이를 갖는다.
  • 부모 노드, 조부모 노드가 아닌 노드는 최소값이 될 수 없다.
    

🧐 자식 노드와 그 직계 상위 노드 간의 차이를 구하자

• 자식 노드가 모든 직계 부모 노드와 연산이 이뤄져야 한다
  ➡️ DFS (Depth First Search)
• 트리의 특성을 이용해, 각 노드 간 탐색을 재귀 구조로 구현한다.

의사 코드

1. 전역 변수 List 를 사용한다.
2. 전역 변수 List에 노드의 값을 삽입한다.
3. 하위 노드로 이동한다.
4. 하위 노드는 List에 저장된 모든 상위 노드와 빼기 연산하며 최소값을 구한다.
5. 하위 노드가 구한 최소값이 상위 노드로 반환된다.
6. 상위노드는 List에 저장된 모든 상위 노드와 빼기 연산하며 최소값을 구한다.
7. 하위 노드의 최소값과 상위 노드의 최소값을 비교해 최소값을 구한다.

int recursive(TreeNode 노드){
	list.add(노드 value);
    int a = recursive(노드 왼쪽 자식);
    int b = recursive(노드 오른쪽 자식);
    if(a>=b) 이전 최소값 = a;
    else 이전 최소값 = b;
    list.remove(노드 value);
    do list에 있는 값과 현재 노드 value와의 min 값 구하기 -> 이번 최소값
    if(이번 최소값 >= 이전 최소값) return 이번 최소값
    else return 이전 최소값
    
}

결과

전체 코드 github 링크

다른 풀이

int min = Integer.MAX_VALUE;
    public int getMinimumDifference(TreeNode root) {
        dfs(root);
        return min;
    }

    private void dfs(TreeNode root) {
        if(root == null) {
            return;
        }

        int minValue = Integer.MAX_VALUE;
        int maxValue = Integer.MIN_VALUE;

        if(root.right != null) {
            minValue = findMin(root.right);
            min = Math.min(min, minValue-root.val);
        }
        if(root.left != null) {
            maxValue = findMax(root.left);
            min = Math.min(min, root.val - maxValue);
        }

        dfs(root.left);
        dfs(root.right);
    }

    private int findMax(TreeNode root) {
        if(root == null) {
            return Integer.MIN_VALUE;
        }
        return Math.max(findMax(root.left), Math.max(findMax(root.right), root.val));
    }

    private int findMin(TreeNode root) {
        if(root == null) {
            return Integer.MAX_VALUE;
        }
        return Math.min(findMin(root.left), Math.min(findMin(root.right), root.val));
    }

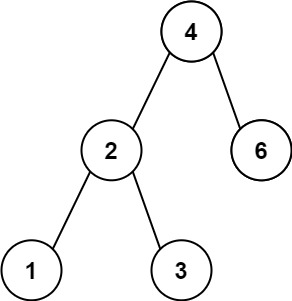
루트 노드와 왼쪽 하위 트리의 노드값의 최소차는 루트 노드의 값과 왼쪽 하위 트리의 최대값 사이의 차이이다.
루트 노드와 오른쪽 하위 트리의 노드값의 최소차는 루트 노드의 값과 오른쪽 하위 트리의 최소값 사이의 차이이다.

그래서 노드를 DFS 하며, 현재 노드에서 왼쪽 하위 트리의 최대값, 현재 노드에서 오른쪽 하위 트리의 최소값을 구한다.

루트 노드와 왼쪽 하위 트리의 최소값은 사실 최소 차이가 될 수 없다.
그런데 나는 모든 하위 노드의 직계 상위 노드를 다 연산하다보니, 불필요한 연산이 추가된다.
그래서 이 부분이 걸렸는데, 이 솔루션은 그런 문제를 해결한다.
또 이진 탐색 트리에 대한 이러한 특징을 다음번에도 활용할 수 있을 것 같다.
저번에 배웠던 min stack을 이용해 볼수도 있을 것 같고, 이 솔루션으로 다시 구현해보면 여러모로 좋을 것 같다.

트리 구조의 탐색을 처음 해봐서 어떤 식으로 구현을 해야할지 헷갈렸는데, 문제를 풀이하며 감을 잡게 된 것 같다.