[LeetCode] 88. Merge Sorted Array

https://leetcode.com/problems/merge-sorted-array

개요

1. 오름차순 정렬된 배열 nums1과 길이 m, nums2와 그 길이 n이 주어진다.
   • nums1 배열의 길이는 m+n 이며, 이중 n은 0으로 패딩되어 있다.
2. nums1에 nums2를 병합해라

문제 해결 아이디어

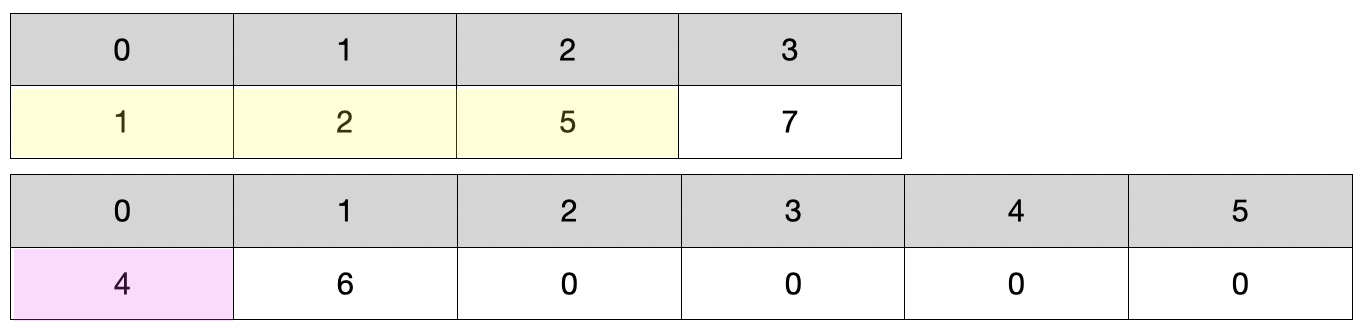
• nums1 = [4, 6, 0, 0, 0, 0], m = 2, nums2 = [1, 2, 5, 7], n = 4 일 때
  

1. nums1[0] 과 nums2[0]를 비교한다.
   nums1[0] 이 nums2[0]보다 크므로 nums1[0] 앞에 삽입한다.
   

2. nums1[1] 과 nums2[1]를 비교한다.
   nums1[1] 이 nums2[1]보다 크므로 nums1[1] 앞에 삽입한다.
   

3. 1) nums1[2] 과 nums2[2]를 비교한다. nums1[1] 이 nums2[2]보다 크지않다.
   2) nums1[3] 과 nums2[2]를 비교한다. nums1[3] 이 nums2[2]보다 크므로 nums1[3] 앞에 삽입한다.
   

4. 1) nums1[4] 과 nums2[3]를 비교한다. nums1[4] 이 nums2[3]보다 크지않다.
   2) nums1을 전부 확인해 비교할 대상이 없으므로, nums2[3]을 nums1[5]에 삽입한다.
   

🧐 nums1 배열에서 nums2[i]가 들어갈 자리를 찾는다

➡️ nums1의 각 원소를 순차적으로 확인하며 nums2[i] 보다 큰지 확인한다.
➡️ nums1의 모든 원소가 확인되어 비교할 대상이 없다면, nums2의 원소를 nums1의 채워지지 않은 부분에 순차적으로 채운다.

의사 코드

1. nums1을 돈다.
2. nums1과 nums2의 값을 비교한다.
   2-1. nums1의 현재값이 nums2의 현재값보다 크다.
   2-1-1. nums1의 현재 인덱스에 nums2의 현재값을 삽입한다.
   2-1-2. nums2의 인덱스를 이동한다.
   2-2-3. nums1이 크기인 변수 m을 +1한다.
   2-2. nums1을 다 검사했다.
   2-2-1. nums1의 현재 인덱스에 nums2의 현재값을 삽입한다.
   2-2-2. nums2의 인덱스를 이동한다.
   2-2-3. nums1이 크기인 변수 m을 +1한다.

while(p = 0 to n){
	if(nums1[i] >= nums2[p]){
    	do nums1[i:m] 인덱스 하나씩 미루기
        nums1[i] = nums2[p]
        p++
        m++
    } else if (i == m) {
    	nums1[i] = nums2[p]
        p++
        m++
    }
    i++
}

결과

전체 코드 github 링크

다른 풀이

public void merge(int[] nums1, int m, int[] nums2, int n) {
    int i = m - 1;
    int j = n - 1;
    int k = m + n - 1;
    while (j >= 0)
      if (i >= 0 && nums1[i] > nums2[j]) 
      	nums1[k--] = nums1[i--];
      else 
      	nums1[k--] = nums2[j--];
  }

이 문제가 유독 어려웠는데 nums1에 더 이상 비교할 원소가 없는 시점을 을 코드로 구현하기가 어려웠다.

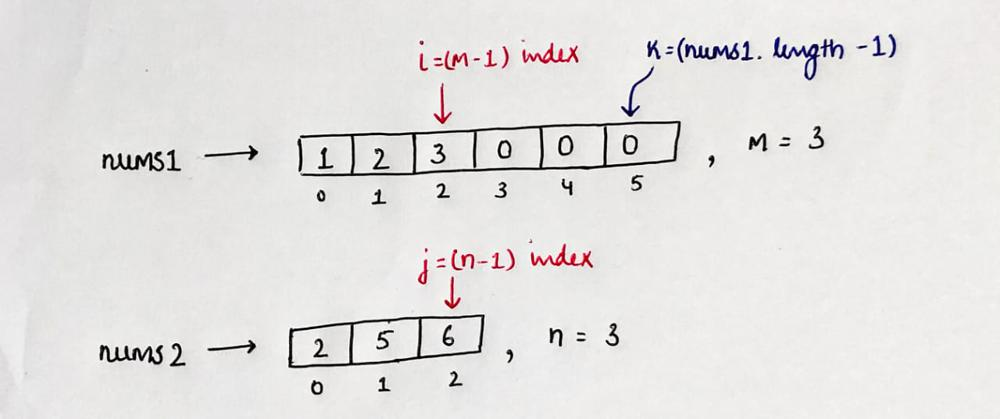
그런데 위와 같이 포인터를
1. nums1의 비교할 대상을 가르키는 포인터
2. nums2의 비교할 대상을 가르키는 포인터
3. nums1의 push할 인덱스를 가르키는 포인터
세 개를 구성하고

가장 뒷 원소부터 순차적으로 비교하는 방향으로 문제를 좀 더 간단하게 풀 수 있었다.

나는 뒷 원소부터 비교하는 방법을 떠올리지 못해서 단순 정렬처럼 nums2가 들어갈 자리를 찾으면 nums1의 인덱스를 하나씩 미루는 코드를 작성했는데,
시간 복잡도 상 효율적이지 못한 것 같다.