[Leetcode] 160. Intersection of Two Linked Lists

문제 바로가기

set을 이용한 visited 체크

1. 방문 여부 체크
   1.1. set에 object id가 있으면 방문했던 노드
   1.2. 아니면 처음 방문한 노드
2. 방문했던 노드면 그 노드가 intersect이다.
   2.1 아니면 set에 object id를 저장 후 재개

Time Complexity: $O(n_A + n_B)$
Time Complexity: $O(n_A + n_B)$

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
        visited = set()
        while headA is not None:
            visited.add(headA)
            headA = headA.next
        while headB is not None:
            if headB in visited:
                return headB
            headB = headB.next
        return
        

cycle check

다음과 같은 linked list에서 headA와 headB가 주어졌다고 하자.

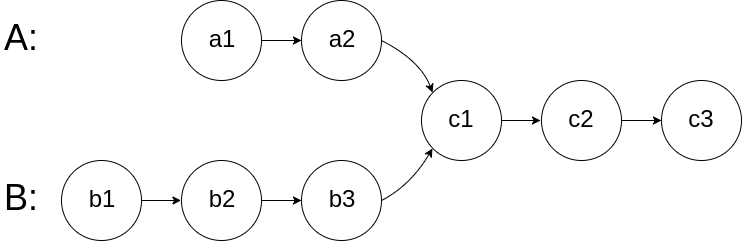
$len_A$, $len_B$, $len_C$를 다음과 같이 정의하자.

• $len_A$: headA가 c1에 도달하기까지 이동해야할 node의 개수
• $len_B$: headB가 c1에 도달하기까지 이동해야할 node의 개수
• $len_C$: c1부터 lead node까지의 node 개수

매 loop에서 headA와 headB가 leaf node를 만날때까지 한 칸씩 전진한다고 하자. 이 때 headA가 이동한 node의 개수는 $len_A + len_C$, headB는 $len_B + len_C$가 될 것이다.
leaf node에서는 headA는 node b1으로, headB는 a1으로 교차 이동해 다시 전진을 시작한다고 했을 때, headA가 $len_B$칸을, headB는 $len_A$칸을 전진하면 두 head의 이동거리가 $len_A + len_B + len_C$로 같아지면서 c1에서 만날 것이다. 따라서 headA와 headB가 같은 node를 가리킬 때까지 전진을 반복하면 된다.

만약 Linked list A와 B가 합류하는 지점이 없다면 어떻게 될까? 각 head는 $len_A + len_B$를 이동하고 headA == headB == None이 되어서 Loop문을 탈출할 것이다.

Time Complexity: $O(n_A + n_B)$
Time Complexity: $O(1)$

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
        pa, pb = headA, headB
        while pa is not pb:
            pa = pa.next if pa is not None else headB
            pb = pb.next if pb is not None else headA
        return pa