[Leetcode] 221. Maximal Square

문제 바로가기

DP

(r, c)의 위치에서 만들 수 있는 1로 이루어진 가장 큰 정사각형을 구해보자.
(r-1, c-1)에서의 최대 정사각형의 변의 길이 $k$를 저장해두었다고 할 때, 현재 위치에서 (r-1, c-1)에서의 최대 정사각형보다 더 큰 정사각형($k$+1)을 가질 수 있기 위해서는 다음의 조건을 만족해야 한다.

1. (r, c)의 값이 1
2. (r, c-$k$-1) ~ (r, c-1)의 값이 모두 1
3. (r-$k$-1, c) ~ (r-1, c)의 값이 모두 1

이 때 2번와 3번 조건 좌표는 이미 탐색을 거친 영역이므로 저장해둔 최대 정사각형 변의 값이 있을 것이다. 따라서 다음과 같은 조건을 만족하게 되면 된다.

1. (r, c)의 값이 1
2. (r, c-1)의 dp 값이 >= $k$
3. (r-1, c)의 dp 값이 >= $k$

만약 2번 혹은 3번의 조건을 만족하지 못해서 둘 중 하나의 dp 값이 $l$이라면 (r, c)에서의 최대 정사각형 변의 값은 $k$+1이 아닌 $l$+1이 될 것이다.
이를 다시 정리한다면 현 위치 (r, c)에서의 최대 값을 다음과 같다.

• if (r, c) 값이 0: 0
• else: 1 + min(dp[r-1][c-1], dp[r-1][c], dp[r][c-1])

Time Complexity: $O(mn)$
Space Complexity: $O(mn)$

class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        m, n = len(matrix), len(matrix[0])
        dp, new_dp = [0] * n, []
        ans = 0
        
        for r in range(m):
            for c in range(n):
                if matrix[r][c] == "0":
                    new_dp.append(0)                    
                elif c == 0:
                    new_dp.append(1)
                else:
                    new_dp.append(1 + min(new_dp[-1], dp[c-1], dp[c]))
            dp, new_dp = new_dp, list()
            ans = max(ans, *dp)
        return ans ** 2

DP + 최적화

사실 DP에서 (r, c)의 dp값을 업데이트할 때 (r-1, c-1), (r-1, c), (r, c-1) 이렇게 3개의 dp값만을 사용한다. 따라서 2차원이 아닌 1차원의 dp만으로도 같은 결과를 얻을 수 있다.

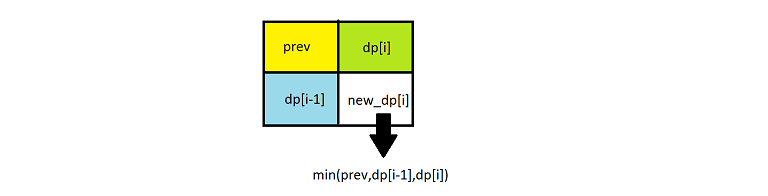
i열의 dp값을 업데이트한다고 할 때, dp[i-1]은 이미 업데이트된 i-1열의 dp 값이고 prev는 업데이트 전 i-1열의 dp 값이 된다.

Time Complexity: $O(mn)$
Space Complexity: $O(n)$

class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        m, n = len(matrix), len(matrix[0])
        dp = [0] * (n + 1) # 열이 0일 때도 참조할 i-1값을 위해 길이를 n+1로 생성한다.
        max_sq_len = 0
        
        prev = 0
        for r in range(m):
            for c in range(n):
                tmp = dp[c+1]
                if matrix[r][c] == "0":
                    dp[c+1] = 0
                else:
                    dp[c+1] = 1 + min(prev, dp[c], dp[c+1])
                prev = tmp
            max_sq_len = max(max_sq_len, *dp)
        return max_sq_len ** 2