[Leetcode] 96. Unique Binary Search Trees

문제 바로가기

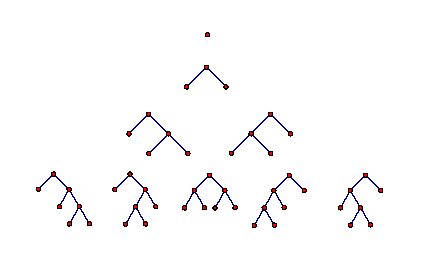
1부터 n까지의 정수들을 담고 있는 n개의 노드들로 구성된 이진탐색트리를 $T_n$이라 하자.
root 노드의 값이 n일 때, 나머지 n-1개의 노드는 전부 root의 왼쪽에 존재한다. 이는 root의 왼쪽 자식으로 $T_{n-1}$을 가지는 것과 같다.
그렇다면 root 노드의 값이 n-1일 때는 왼쪽에는 $T_{n-2}$가 오른쪽에는 n을 값으로 가지는 노드가 하나 존재한다.

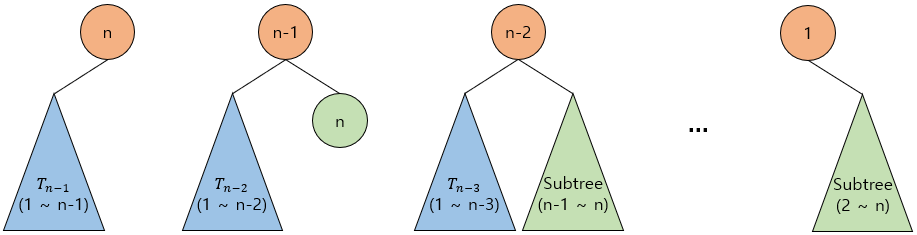
이 때, n-1 ~ n값을 가지는 subtree와 1 ~ 2를 가지는 $T_2$는 노드의 값은 다르지만 트리의 구조는 동일하다. 따라서 다음과 같이 표현할 수 있다.

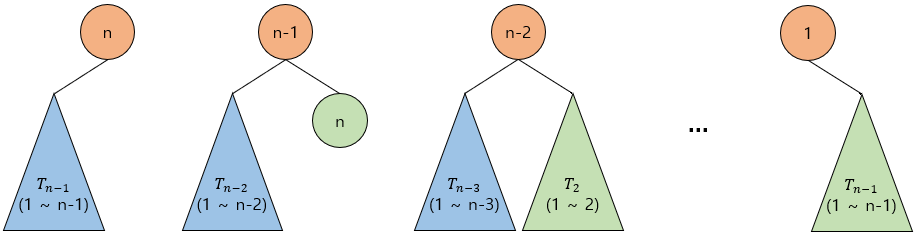
따라서 다음과 같은 점화식을 얻어 문제를 해결할 수 있다.
$T_n=\sum_{k=1}^n T_kT_{n-1-k}$

Top down

Time Complexity: $O(n^2)$
Space Complexity: $O(n)$

class Solution:
    def numTrees(self, n: int) -> int:
        dp = [0 for _ in range(n + 1)]
        dp[0], dp[1] = 1, 1
        
        def backtrack(n: int) -> int:
            if not dp[n]:
                res = 0
                for i in range(n//2):
                    res += backtrack(i) * backtrack(n-1-i)
                res *= 2
                
                if n % 2:
                    # odd
                    res += backtrack(n//2) ** 2

                dp[n] = res
            
            return dp[n]
        
        return backtrack(n)

Bottom up

Time Complexity: $O(n^2)$
Space Complexity: $O(n)$

class Solution:
    def numTrees(self, n: int) -> int:
        #dp tabulation
        if n==1:
            return 1
        dp=[1 for i in range(n+1)]
        dp[1]=1
        for nodes in range(2,n+1):
            ans=0
            for leftnodes in range(0,nodes):
                ans+=dp[leftnodes]*dp[nodes-1-leftnodes]
            dp[nodes]=ans
        return dp[n]

카탈란 수 (Catalan number)

정의

조합론에서 이진 트리의 수 따위를 셀 때 등장하는 수열이다.
음이 아닌 정수 n에 대해서, n 번째 카탈란 수 Cn은 다음과 같다.
$C_n=\dfrac{1}{n+1}\dbinom{2n}{n}=\dfrac{(2n)!}{n!(n+1)!}$

카탈란 수는 자연수열이며, n=0…37까지의 값들은 아래와 같다. (OEIS의 수열 A000108)

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, 18367353072152, 69533550916004, 263747951750360, 1002242216651368, 3814986502092304, 14544636039226909, 55534064877048198, 212336130412243110, 812944042149730764, 3116285494907301262, 11959798385860453492, 45950804324621742364, …

적용 예시

$C_n$은 -1과 1 값으로 만들어진 수열 $(a_1, a_2, \ldots, a_{2n})$에서 $a_1+a_2+\ldots+a_{2n}=0$일 때, 각각의 부분합 $a_1, a_1+a_2, \ldots, a_1+a_2+\ldots+a_{2n}$이 모두 0 이상이 되도록 하는 방법의 수이다.

$C_n$은 길이가 2n인 모든 뒤크 단어(영어: Dyck word)의 개수이다.

발터 폰 뒤크(독일어: Walther von Dyck)의 이름을 딴 뒤크 단어는 n개의 X와 n개의 Y로 이루어진 문자열 중 처음부터 X와 Y의 개수를 세었을 때 항상 X가 Y보다 많거나 같은 것을 가리킨다.

예를 들면, 아래의 예제는 길이가 6인 모든 뒤크 단어들을 나열한 것이다.
XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY.

뒤크 단어에서 X를 여는 괄호로 보고 Y를 닫는 괄호로 보면, Cn은 n쌍의 괄호로 만들 수 있는 올바른 괄호 구조의 개수이다.
((())) ()(()) ()()() (())() (()())

$C_n$은 n + 1개의 항에 괄호를 씌우는 모든 경우의 수이다. 혹은 n + 1개의 항에 이항연산자를 적용하는 순서의 모든 가지수로도 볼 수 있다.

이항연산자의 적용 순서는 이진 트리로도 나타낼 수 있다. 따라서 $C_n$은 n + 1개의 단말 노드를 갖는 이진 순서 트리의 개수임을 알 수 있다.

$C_n$은 동형이 아닌 모든 정 이진 트리 가운데 자식을 가진 노드(internal vertex, 혹은 branch라고 부르는)가 n개인 트리의 개수이다. (정 이진 트리는 한 개의 자식만 가진 노드가 없고, 모든 노드가 두 개의 자식을 가졌거나 혹은 단말 노드인 트리를 가리킨다.)

참고

• 카탈란 수: 블로그 바로가기