Critical instant 증명

앞서 포스팅했던 논문 Scheduling Algorithm for Multiprogramming in a Hard-Real-Time Environment을 읽으면서 선배와 함께 해봤던 증명을 정리한 내용이다. 사실 수식을 아직 온전히 다 옮기지 못해서 미완이다! 😅

증명 쓸 때 주의할 점

• 읽는 사람을 생각하면서 많이 풀어서 설명하기
• notation은 최대한 적게 쓰기

논문 읽을 때 주의할 점

• 해결하고자 하는 문제를 무엇으로 정의했는지
• 해당 문제를 해결하기 위해서 어떤 접근법을 사용했는지
• 나라면 어떻게 접근했을 것 같은지 생각하면서
• 증명할 때는 쉬운 케이스 $\rightarrow$ general case $\rightarrow$ corner case 확인

---

Theorem 1

Given a set of two tasks denoted as $\tau_1=(T_1, C_1)$ and $\tau_2=(T_2, C_2)$, where $T_i$ denotes the period of the task $\tau_i$, and $C_i$ denotes the worst-case exeucution time of the task $\tau_i$ (1 $\le i \le$ 2).
Suppose that the task set is scheduled with RM (Rate-Monotonic) algorithm. If the priority of the task $\tau_1$ is higher than the priority of the task $\tau_2$ (i.e. $T_1<T_2$), then the critical point of task $\tau_2$ starts simultaneously with the task $\tau_1$.

Proof

Assume there exist a time point $\epsilon$ where amount of the preemption by the task $\tau_1$ is larger than the point described above (simultaneously relased).
Let us suppose the amount of cumulative execution time of the task $\tau_1$ at the time point $k$ as the function $f(k)$, then $f(k)$ can be represented as follows.
Here, $\epsilon$ is a variation factor for $\tau_1$ initiation time. ($0 \le \alpha<T_1$) $\tau_1$ is initiated at times $\epsilon+kT_1 , k\ge0$. $\epsilon$ is 0 with described case.

$f'(\epsilon) = C_1 \lfloor\frac{T_2 - \epsilon}{T_1}\rfloor + \min(C_1, T_2-T_1\lfloor\frac{T_2 - \epsilon}{T_1}\rfloor-\epsilon)$

I'll show in every case, $f(0) > f(\epsilon)$, which means $\tau_2$ have critical instant when initiated with $\tau_1$.

Correctness of $f(t)$

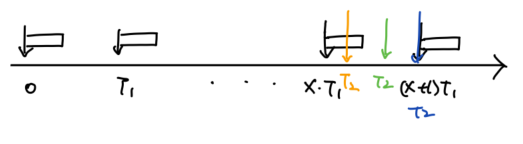
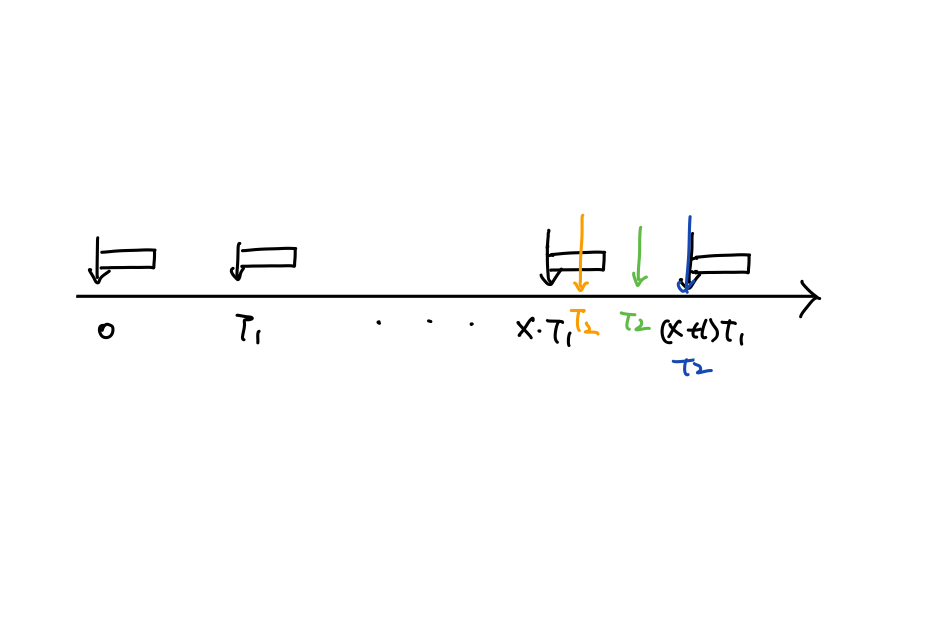
위의 그림과 같이 time 0에 task $\tau_1$과 $\tau_2$가 함께 release 되었을 때 task $\tau_2$의 $T_2$가 가질 수 있는 경우의 수는 3가지이다.

1. $C_1$과 $T_2$가 overlap되는 상황 (주황색)

   • $f(t)= C_1 \lfloor\frac{T_2}{T_1}\rfloor +T_2-T_1\lfloor\frac{T_2}{T_1}\rfloor$

2. $C_1$과 $T_2$ overlap되지않는 상황 (연두색)

   • $f(t)= C_1 \lfloor\frac{T_2}{T_1}\rfloor +C_1$

3. $\lfloor \frac{T_2}{T_1} \rfloor=\frac{T_2}{T_1}$ , $T_2=k\cdot T_1(k\in\mathbb Z^+)$ (파란색)
   - $f(t)= C_1 \lfloor\frac{T_2}{T_1}\rfloor$

   • 사실 이 케이스도 1번 케이스(주황색)으로 간주할 수 있다.

   // TODO : try extending range of $\epsilon$ to $(-T_2, T_2)$ and show $\ge$
   // TODO : add description of proof