안정적 그 자체, Merge Sort

개요

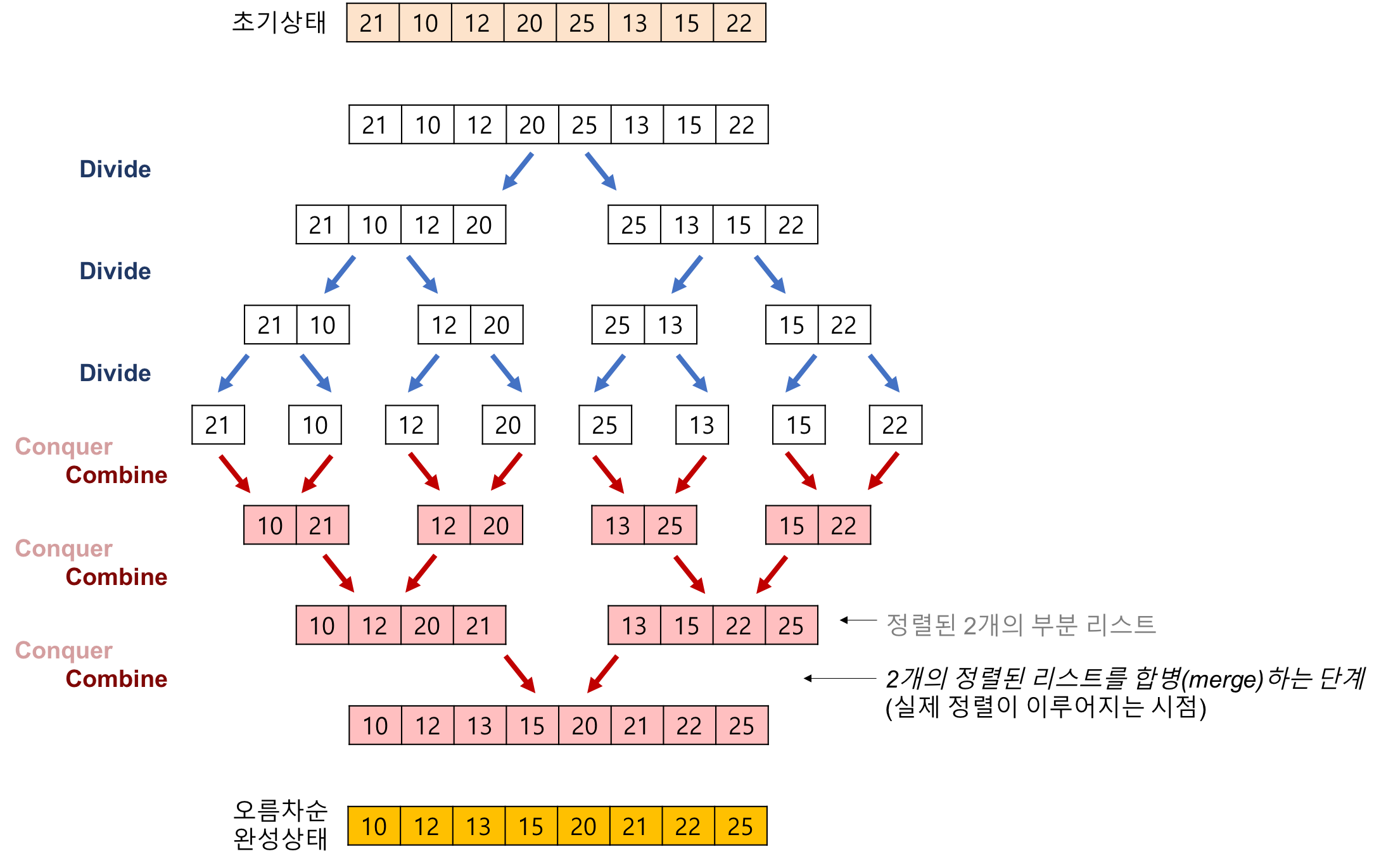
병합 정렬은 배열을 쪼갠 뒤, 다시 병합시키면서 차근차근 정렬해나가는 방식을 사용한다. 이 때 배열을 쪼개는 로직은 퀵 소트와 비슷하다.

이는 퀵 소트와 마찬가지로 분할 정복 기법을 통해 구현하게 된다. 병합 정렬 알고리즘도 속도가 매우 빠르기 때문에 퀵 소트와 함께 많이 언급되는 정렬 방식이다. 퀵 소트와 다른 점이라면 병합 정렬은 안정 정렬에 속한다는 점 정도. (즉, 정렬 후에도 같은 값을 가진 원소간의 순서가 바뀌지 않음을 보장한다.)

로직

1. 배열을 쪼갤 수 없을 때까지 계속하여 분할한다.
2. 더 이상 쪼갤 수 없을 때, 왼쪽 배열과 오른쪽 배열을 정렬하여 병합한다.
   1. 이 때, 정렬된 리스트를 도출하기 위해 새로운 리스트를 생성한다.
   2. 두 배열 값들을 처음부터 하나씩 비교해가며 더 작은 값을 새로운 리스트에 추가한다.
   3. 만약 하나의 배열이 먼저 소진됐다면 남은 배열의 값들을 왕창 추가한다.
   4. 새로운 리스트를 기존의 리스트에 반영한다.
3. 2번 작업을 원본 배열 크기가 될 때까지 재귀적으로 반복한다.

이를 코드로 옮겨보면, 아래와 같은 모양이다. (코틀린 기준)

fun mergeSort(data: MutableList<Int>, start: Int, end: Int) {
    if (start >= end) return

    val mid = (start + end) / 2  // 반으로 쪼갬
    mergeSort(data, start, mid)
    mergeSort(data, mid + 1, end)

    merge(data, start, mid, end)  // 분할된 두 리스트을 하나로 정렬하며 합침
}

fun merge(data: MutableList<Int>, start: Int, mid: Int, end: Int) {
    val sortedList = mutableListOf<Int>()  // 정렬된 새로운 리스트
    var indexA = start  // 왼쪽 배열 인덱스
    var indexB = mid + 1  // 오른쪽 배열 인덱스

    while (indexA <= mid && indexB <= end) {  // 두 리스트 중 하나라도 모두 소진되면 종료
        // 둘 중 최솟값을 새로운 리스트에 담아주는 작업
        if (data[indexA] <= data[indexB]) {
            sortedList.add(data[indexA])
            indexA++
        } else {
            sortedList.add(data[indexB])
            indexB++
        }
    }

    if (indexA > mid) {  // 오른쪽 배열 원소가 아직 남았다면
        for (i in indexB..end) {
            sortedList.add(data[i])
        }
    }

    if (indexB > end) {  // 왼쪽 배열 원소가 아직 남았다면
        for (i in indexA..mid) {
            sortedList.add(data[i])
        }
    }

    for (x in sortedList.indices) {  // 정렬된 부분 대입
        data[start + x] = sortedList[x]
    }
}

fun main() {
    val data = mutableListOf(9, 8, 7, 6, 5, 4, 3, 2, 1)
    mergeSort(data, 0, data.size - 1)
    println(data)
}

퀵 소트와의 차이점은 이렇다. 퀵 소트는 피벗을 통해 정렬 (Partition) 을 한 뒤 배열을 쪼갠다면, 병합 정렬은 배열을 쪼갤 수 있을 만큼 끝까지 쪼갠 뒤에, 이를 합쳐가며 물 흐르듯 정렬 (Merge) 하는 느낌이다.

시간 복잡도

데이터의 분포와 전혀 상관없이 항상 1/2 로 쪼개기 때문에 호출 깊이는 O(logn) 이 되고, 각 병합 단계에 있어 원소 비교 연산 (N) 이 필요하기 때문에 이를 곱하여 총 O(nlogn) 이 소요된다. 이미 정렬되어 있는 두 영역에 대해 병합을 하기 때문에, 순차적으로 비교하여 정렬할 수 있다는 장점이 있다.

공간 복잡도

정렬하여 병합하는 과정에서 새로운 리스트를 만드는 모습을 확인했다. 이 때 O(nlogn) 만큼의 공간 복잡도를 차지한다.

장단점 살펴보기

장점

• 안정적인 정렬 알고리즘임
• 데이터의 분포와 관계없이 시간 복잡도가 동일한 것이 가장 큰 장점

단점

• 구현이 다소 복잡함
• 배열을 병합하는 과정에서 임시 배열이 필요함 (공간 복잡도 상당함)

번외) LinkedList 에서의 Merge Sorting

병합 정렬은 순차적인 비교를 통해 정렬하기 때문에, 순차 접근에 용이한 LinkedList 의 정렬이 필요할 때 매우 효율적으로 동작하게 된다. 퀵 소트는 순차 접근이 아닌 임의 접근을 통해 정렬을 하기 때문에 오버헤드가 발생하여 성능이 좋지 않다.