정렬 세계관 최강자, Quick Sort

퀵 소트는 이름에서 풍기는 자신감이 돋보인다(?). 웬만한 상황에선 가장 빠른 속도를 자랑하는 정렬 알고리즘이다. 이번 포스팅에선 이 퀵 정렬 알고리즘이 어떻게 동작하게 되는지, 최선의 경우와 최악의 경우 시간 복잡도는 어떻게 되는지에 대해 알아보자.

개요

퀵 소트는 분할 정복 기법을 통해 데이터를 정렬하는 녀석이다. 분할 정복(Divide and Conquer) 는 말 그대로, 어떤 문제를 반+반으로 쪼개어 각각을 해결 한 뒤에 다시 하나로 모아서 원래 문제를 해결하는 기법이다. 분할을 하고, 그 분할된 문제들 각각을 정복하여 원래 해결하고자 했던 문제를 해결하는 것이다.

퀵 소트는 원소 간의 비교만으로 정렬을 수행하는 알고리즘이기 때문에 비교 정렬의 한 종류이고, 불안정 정렬에 속한 다. 또 한 가지 특징이라면, 분할정복을 활용하는 다른 정렬 알고리즘인 Merge Sort 와 다르게 분할되는 배열이 불균등하다. (즉, 분할해놓고 보니 두 배열의 크기가 일치하지 않는다는 뜻)

🤔 불안정한 정렬 알고리즘이란?

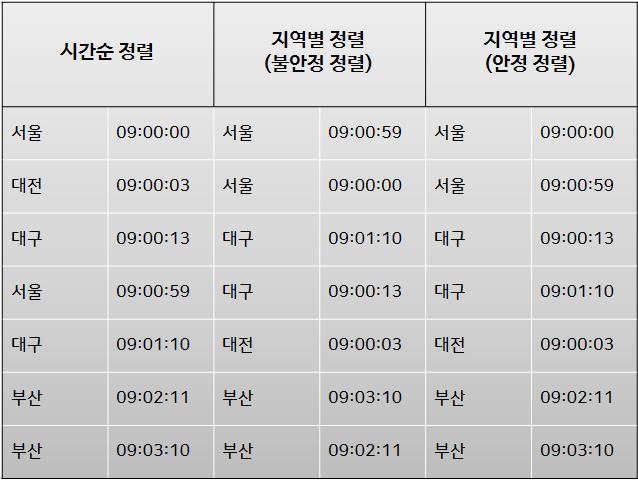
정렬 이후 데이터의 순서가 정렬 이전 원래 순서와 같음을 보장하지 못하는 정렬 알고리즘
아래 사진을 통해 불안정 정렬과 안정 정렬의 차이를 이해해볼 수 있다.

로직

1. 주어진 배열에서 임의의 한 원소를 고르고, 이를 피벗(Pivot) 이라 칭한다. (배열 한 가운데, 맨 앞 원소 등)

2. 피벗을 기준으로 피벗보다 값이 작은 원소들을 싸그리 모아놓은 배열 하나와, 피벗보다 값이 큰 원소들을 싸그리 모아놓은 배열 하나 → 이렇게 배열을 둘로 나눈다. 분할을 마친 뒤 피벗은 그 자리에서 더이상 움직이지 않는다.

3. 분할된 두 개의 배열에 대해 위 1, 2 과정을 재귀적으로 반복한다.

이렇게 하면, 1-2 과정을 한 번 수행할 때마다 피벗 원소의 자리가 고정되기 때문에 반드시 정렬이 언젠가 완수된다는 것을 보장할 수 있다.

위 로직에 따라, 코드를 작성해보면 아래와 같이 해볼 수 있을 것이다. (파이썬 기준)

array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]

def quick_sort(array):
    if len(array) <= 1:  # 길이가 1까지 도달한 경우 고대로 리턴
        return array

    pivot = array[0]  # 이 경우, 첫 원소를 피벗으로 삼음
    tail = array[1:]  # 피벗 제외 배열 슬라이싱

    left_side = [x for x in tail if x <= pivot]  # 피벗보다 작거나 같은 원소만 모은 배열 
    right_side = [x for x in tail if x > pivot]  # 피벗보다 큰 원소만 모은 배열

    # 피벗의 자리는 결정되었고, 피벗 기준 왼쪽 배열과 오른쪽 배열에 대해 재귀 수행
    return quick_sort(left_side) + [pivot] + quick_sort(right_side)

print(quick_sort(array))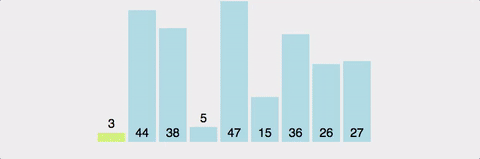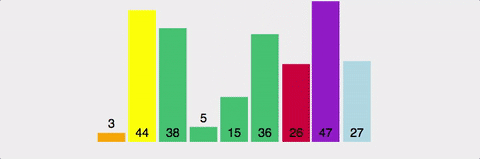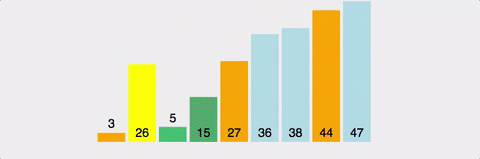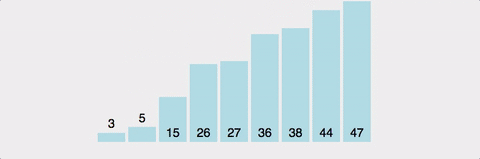

상황별 시간 복잡도 따져보기

최선의 경우

최선의 경우에 퀵 소트는 O(nlogn) 속도로 동작하게 된다. 이유는 다음과 같다.

1️⃣ 비교 횟수 : O(nlogn)

원소 개수 N 이 2의 거듭제곱이라고 가정했을 때 (n = 2^k), 예를 들어 n = 8 인 경우 (n = 2 ^ 3)

2^3 → 2^2 → 2^1 → 2^0 순으로 줄어들어, Recursive 깊이가 3임을 알 수 있다.

이것을 일반화 하게 되면, n = 2^k 라고 가정했을 때 k = log₂n 임을 알 수 있다.

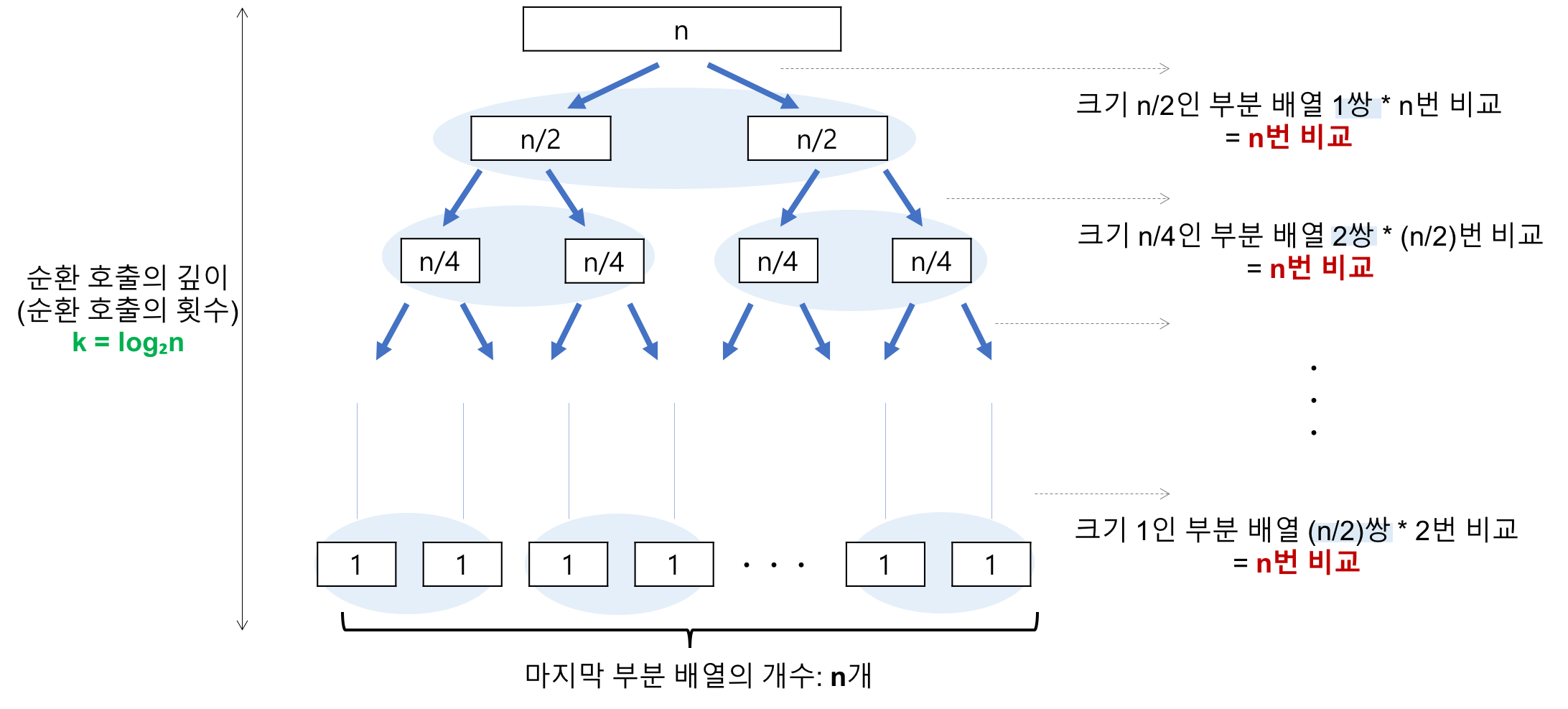
2️⃣ 각 Recursive 호출 단계의 비교 연산 : O(n)

순환 호출 각각에서는 피벗과 전체 원소들 각각을 비교해야 하기 때문에, 평균적으로 n 번 비교가 발생한다.

따라서, 이러한 연산 복잡도를 종합해보았을 때 O(nlogn) 이 나오게 되는 것이다.

최악의 경우

퀵 소트에 있어서, 정렬하고자 하는 배열이 오름차순 혹은 내림차순으로 정렬되어 있을 때가 최악의 경우이다. 이 경우 시간 복잡도가 O(n^2) 까지 치솟게 된다. (닉값 못한다)

1️⃣ 비교 횟수 : O(n)

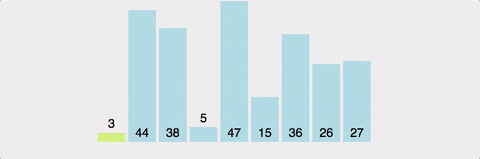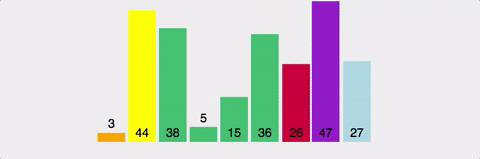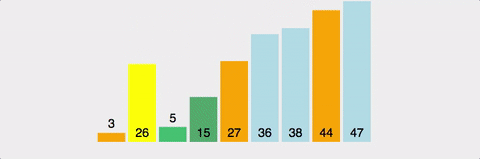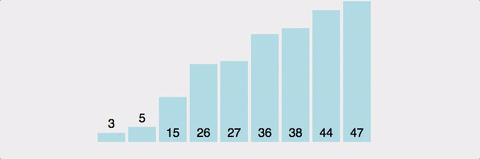
배열이 정렬되어 있기 때문에, 계속하여 아래와 같은 형태로 분할되고 말 것이다.

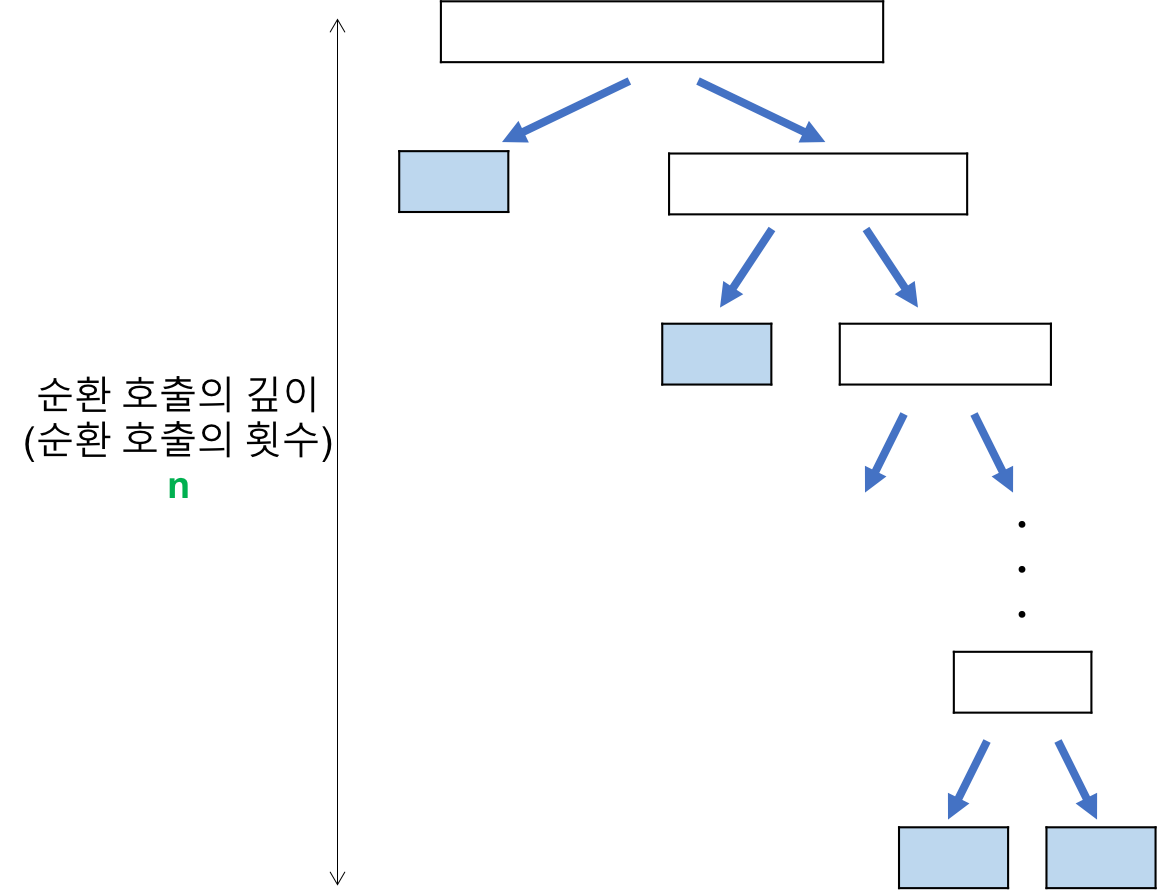
원소 개수가 n 이라고 하면, 순환 호출 깊이 역시 n 이 된다.

2️⃣ 각 Recursive 호출 단계의 비교 연산 : O(n)

아까 위에서 다룬 최적의 상황과 같은 맥락으로, O(n) 만큼 소요된다.

따라서, 최악의 경우 O(n^2) 이 소요된다.

(사실 정렬된 배열을 정렬하는 상황이 왜 있겠나 싶다)

공간 복잡도

뭐, 딱히 다른 테이블을 선언하고 그런 것이 아니고 정해진 배열 내에서 원소가 왔다갔다 하는 것이기 때문에 원소 개수 n 만큼, 즉 O(n) 을 차지한다.

장단점 살펴보기

장점

• 필요한 자리 교환 연산만 수행하기 때문에 웬만하면 O(nlogn) 이 나오는 것 자체가 아주 이상적임
• 다른 메모리 공간을 차지하지 않기 때문에 공간 복잡도 또한 우수함
  • 단, 위에서 소개한 코드는 퀵 소트 개념을 소개하는 코드일 뿐 공간 복잡도는 고려 안 됨

단점

• 불안정한 정렬 알고리즘임
• 이미 정렬된 상태에서 수행할 시 불균형 분할에 의해 O(n^2) 까지 성능이 안 좋아짐

---