Chapter 1-5 Searching an Ordered Array

1) 탐색 알고리즘 A

• Strategy

- Input data and Data structure : unsorted array
- sequential search

• Algorithm

int seqSearch(int[] E, int n, int K)
    int ans, index;
    ans = -1; // Assume failure
    for(index = 0; index < n; index++)
    	if(K == E[index])
           ans = index; // Success!
           break; // Done!
    return ans;

• Analysis A

- W(n) = n 
- A(n) = q[(n+1)/2] + (1-q)n
	(K가 array의 마지막이거나, 존재하지 않을 때 평균 수행시간)

• Optimality A

- F(n) = n이므로 Algorithm A는 Optimal 하다.

---

2) 탐색 알고리즘 B

• Strategy

- Input data and Data structure : 오름차순으로 정렬된 Array
- sequential search

• Algorithm

- int seqSearch(int[] E, int n, int K) 
  A와 동일

• Analysis B

- W(n) = n 
- A(n) = q[(n+1)/2] + (1-q)n
  A와 알고리즘이 같으므로 분석내용 또한 같다

• Optimality B

 정렬되었음을 그닥 활용하지 않아 효율성은 없다.

---

3) 탐색 알고리즘 C

• Strategy

- Input data and Data structure : 오름차순으로 정렬된 Array
- sequential search : 
  entry에서 K보다 큰 값을 만나면 알고리즘을 종료한다.

• Algorithm

int seqSearchMod(int[] E, int n, int K) 
  int ans, index;
  ans = -1; // Assume failure
  for(index = 0; index < n; index++)
  	if(K>E[index]) continue;
    	if(K<E[index]) break; //Done!
    	//K==E[index]
        ans = index; //Find it
        break;
  return ans;

• Analysis C
  

---

4) 탐색 알고리즘 D : Binary Search

• Strategy

- K값을 array의 중간값과 비교한다
- 한번의 비교에 entry의 나머지 절반을 제거한다.
- 같은 전략을 재귀적으로 반복한다.

• Algorithm

- Input : first, last (살펴볼 index의 처음과 끝), K, 
정렬된 배열 내에서 index 값이 first와 last 사이에 있는 모든 정수
- Output : K가 존재하는 index값, 혹은 E안에 K가 없을 때 나오는 결과 -1
- 반드시 정렬 된 array에서만 사용한다.

int binarySearch(int[] E, int first, int last, int K)
    if(last < first) // base case
    	index = -1;   // 재귀문을 탈출할 수 있도록 하는 조건
    else
    	int mid = (first + last) / 2;
        if (K == E[mid]) index = mid;
        else if(K < E[mid]) index = binarySearch(E, first, mid-1, K)
        else index = binarySearch(E, mid+1, last, K)
    return index

• Worst Case Analysis
  Binary Search 알고리즘의 경우 비교를 한 번 시행할 때 마다 entry의 원소가 절반씩 줄어든다.
  최악의 경우 원소가 1개가 남을 때 까지 이를 계속 반복하므로 최악의 경우의 원소의 개수는
  n x $\frac{1}{2}$ x $\frac{1}{2}$ x ... x $\frac{1}{2}$ = 1
  1이 남을 때 까지 $\frac{1}{2}$을 곱한 횟수를 d 라고 하면
  n x $\frac{1}{2} ^ d$ = 1 / d = $\log_2 n$ 이 되고, 최종적으로
  $W(n)$ = $\log_2 n$ + 1(recursive 호출하기 전에 비교한 것)

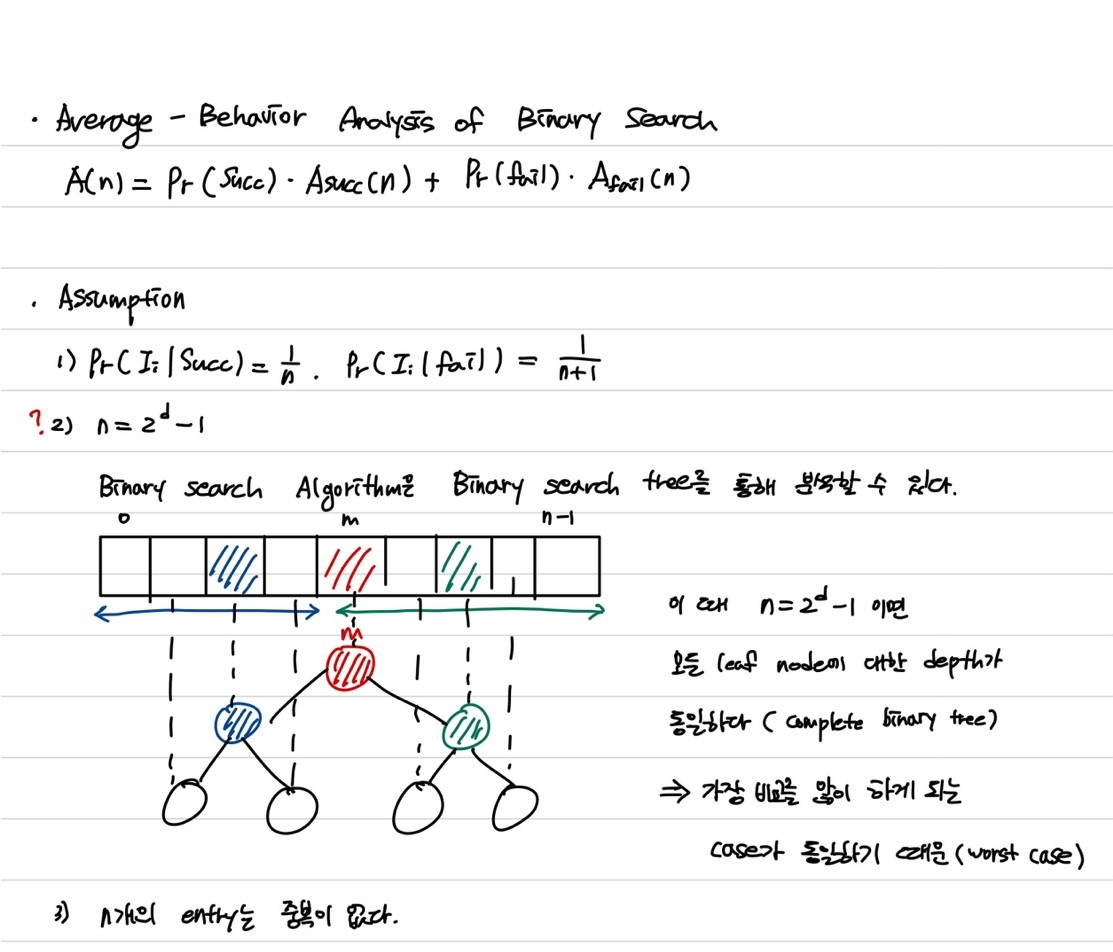
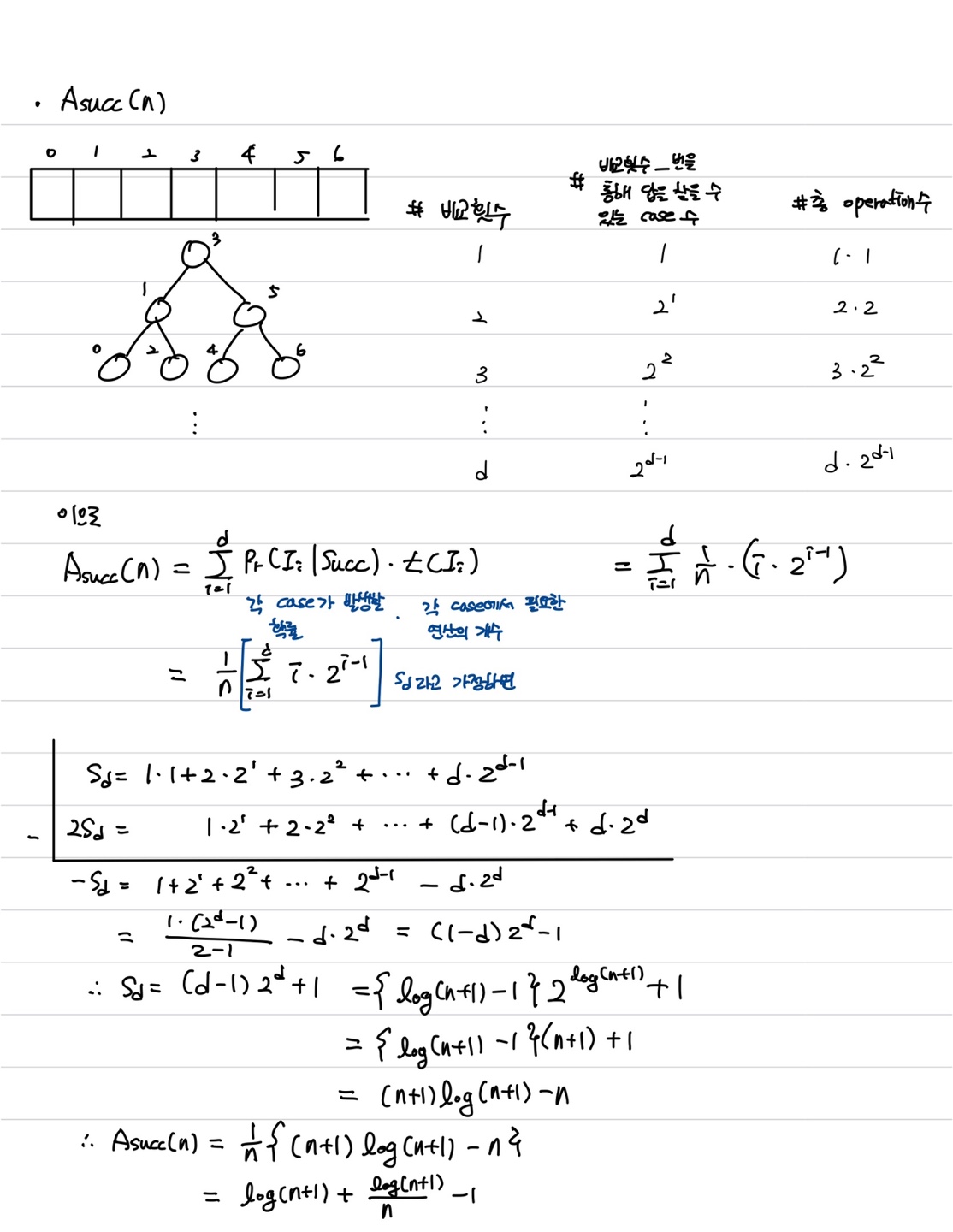
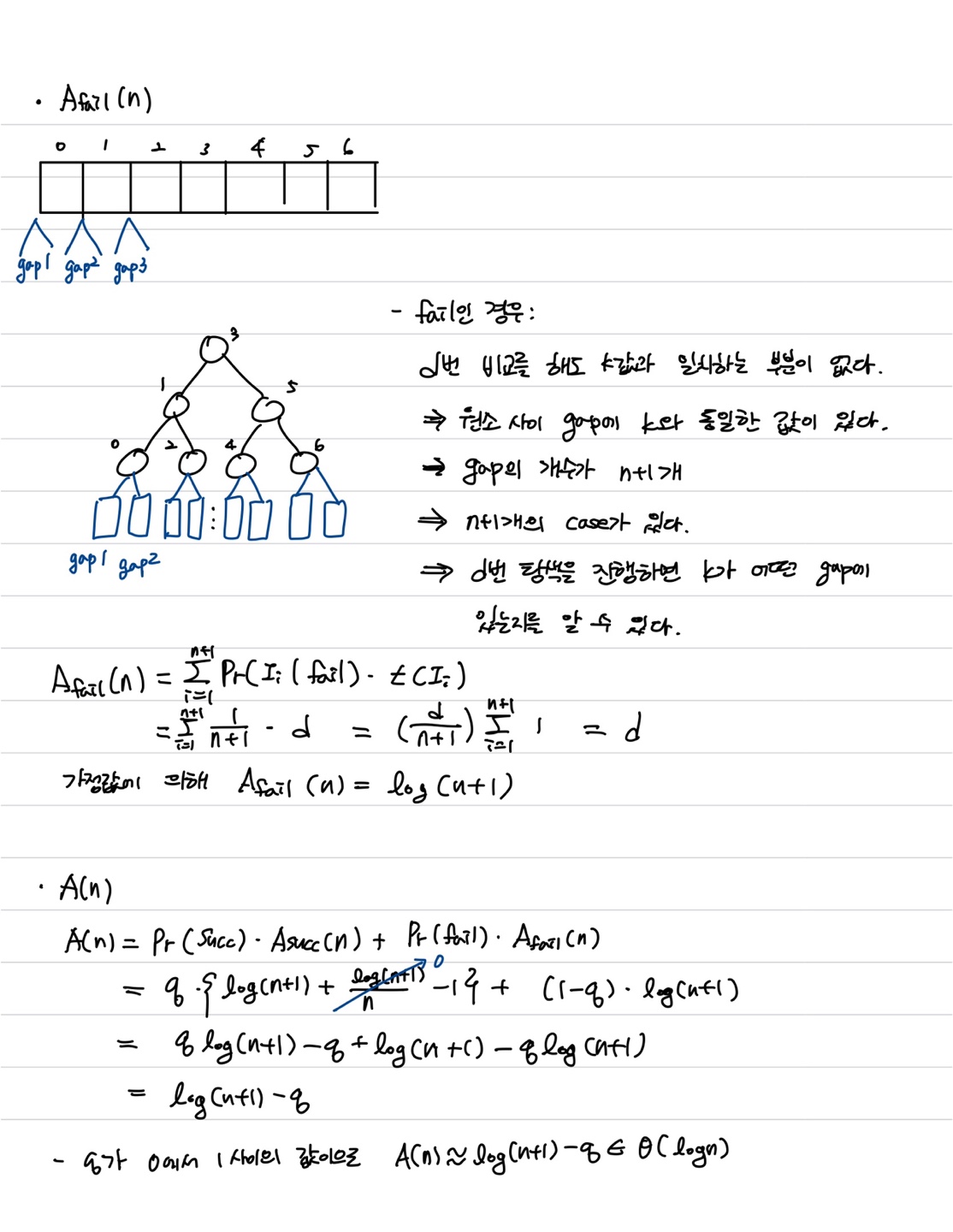
• Average-Behavior Analysis of Binary Search