개념
나눗셈 과정에서 나누어지는 수는 Dividend(피제수), 피제수를 나누는 수는 Divisor(제수)라고 부르고, 나눗셈의 결과로는 Quotient(몫)과 Remainder(나머지)가 있다.
즉, dividend = quotient * divisor + remainder 라고 할 수 있다.
나눗셈 알고리즘도 곱셈과 마찬가지로 두 가지 버전이 있다.
나눗셈 하드웨어 1
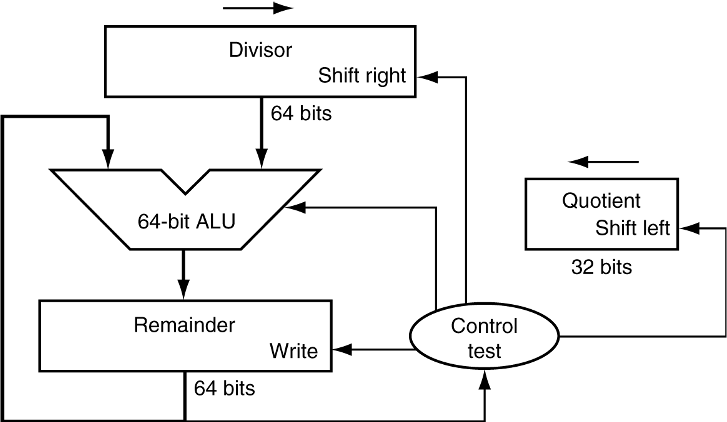
첫 번째 버전은 Divisor 레지스터, ALU, Remainder 레지스터는 모두 64비트이고, Quotient 레지스터만 32비트인 경우이다.
Divisor가 n bit이라면 n+1번 반복하게 되는데, Remainder의 값이 음수인지 양수인지에 따라 수행하는 작업이 달라진다.
- Remainer를 Dividend 값으로 초기화한다.
- Remainder = Remainder - Divisor
- Remainder의 부호를 확인한다.
3-1. Remainder < 0 이라면, Divisor을 빼기 전으로 복원한 후, Quotient(몫)을 왼쪽으로 1bit 이동하고, Quotient의 LSB = 0
3-2. Remainder >= 0 이라면, 연산을 수행하지 않고, Quotient를 왼쪽으로 1bit 이동하고 Quotient의 LSB = 1- Divisor을 오른쪽으로 1bit 이동한다.
예제
7 나누기 2를 계산하되, 공간을 절약하기 위해 4비트 알고리즘을 이용하여 0000 0111 나누기 0010 로 하라.
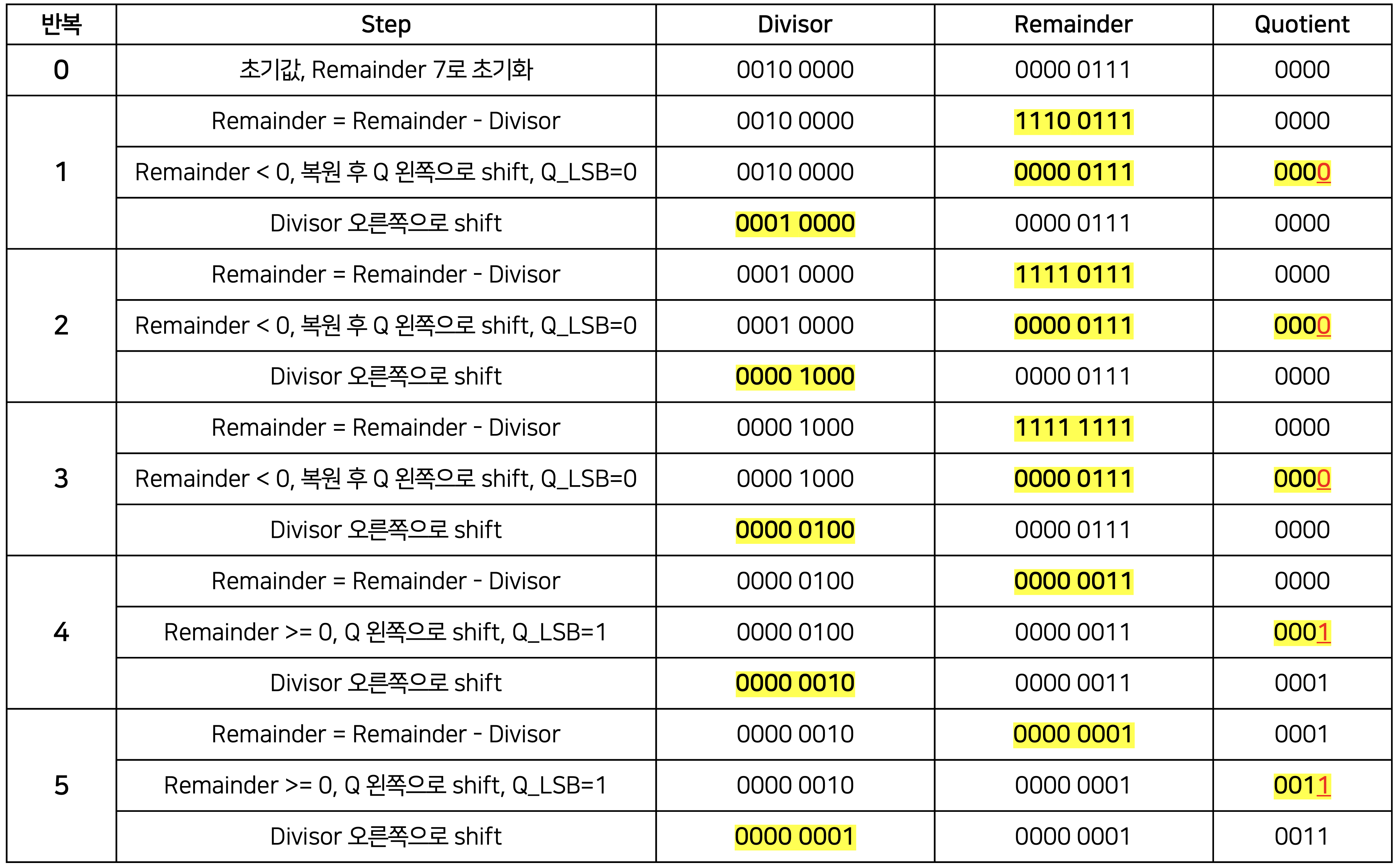
따라서 계산 결과는 Remainder(나머지)는 0000 0001 이고, Quotient(몫)는 0011 이다.
검산을 해보면, 7 나누기 2의 결과는 몫은 3(0011), 나머지는 1(0001)이므로 결과가 일치한다.
나눗셈 하드웨어 2
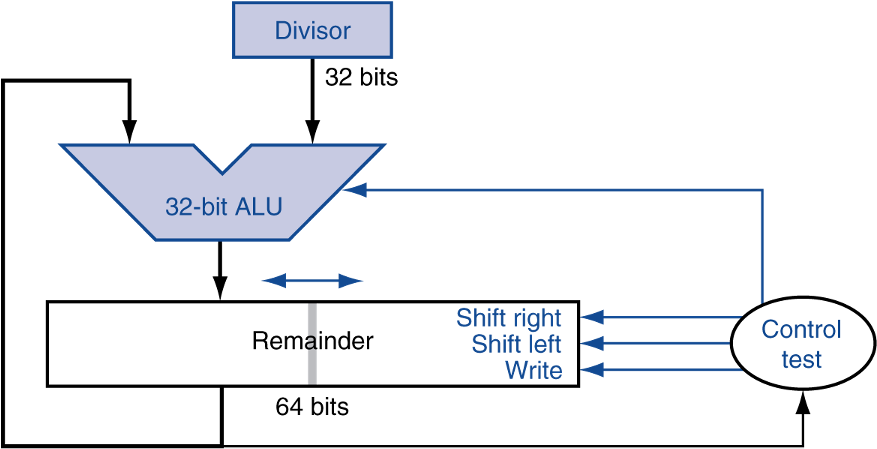
두 번째 버전은 Divisor 레지스터, ALU, Quotient 레지스터는 모두 32비트이고, Remainder 레지스터만 64비트인 경우이다. 별도의 Quotient 레지스터가 사라지고, Quotient을 Remainder 레지스터의 오른쪽 절반에 넣는다.
Divisor가 n bit이라면 n번 반복하게 되는데, Remainder의 값이 음수인지 양수인지에 따라 수행하는 작업이 달라진다.
- Remainer / Quotient를 왼쪽으로 1bit 이동한다.
- Remainder = Remainder - Divisor
- Remainder의 부호를 확인한다.
3-1. Remainder < 0 이라면, Divisor을 빼기 전으로 복원한다.
3-2. Remainder >= 0 이라면, 연산을 수행하지 않고, Quotient의 LSB = 1
이 알고리즘은 Optimized Divider로 뺄셈과 동시의 피연산자와 몫을 자리이동시킴으로써 성능 향상이 가능하다.
예제
7 나누기 2를 계산하되, 공간을 절약하기 위해 4비트 알고리즘을 이용하여 0000 0111 나누기 0010 로 하라.
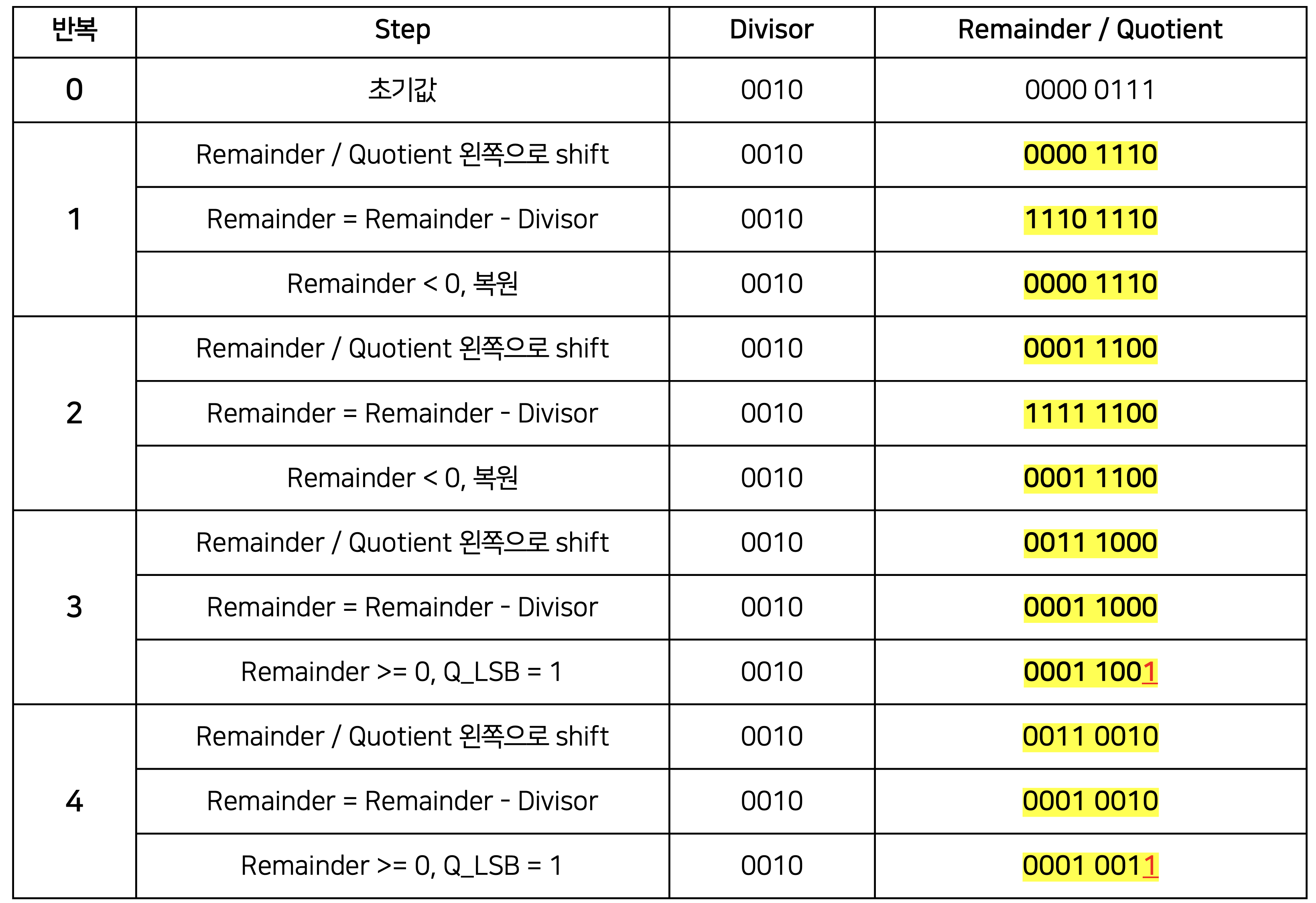
따라서 계산 결과는 Remainder(나머지)는 0001 이고, Quotient(몫)는 0011 이다.
검산을 해보면, 7 나누기 2의 결과는 몫은 3(0011), 나머지는 1(0001)이므로 결과가 일치한다.
요약
Dividend = Quotient * Divisor + Remainder
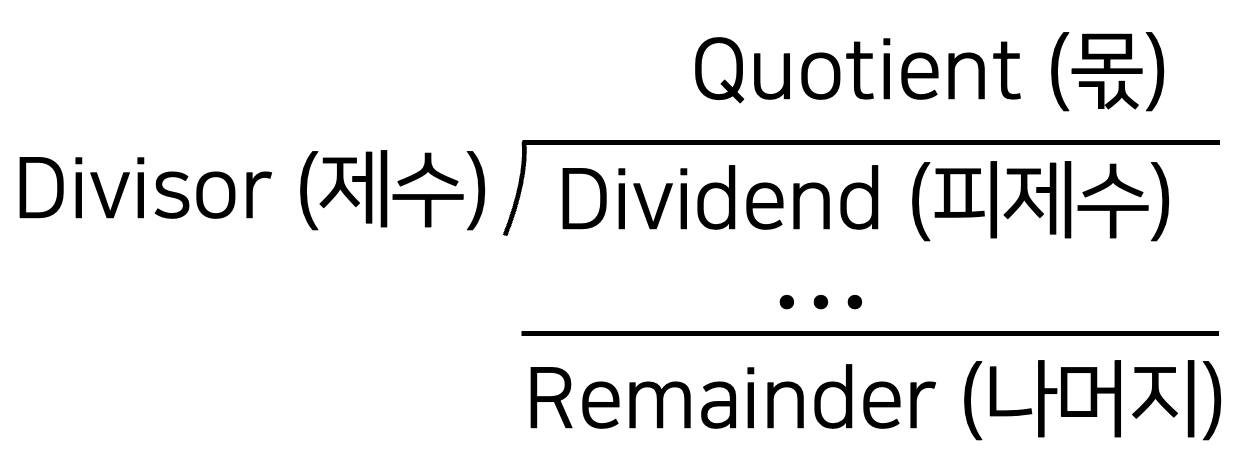
Division
- Remainer를 Dividend 값으로 초기화한다.
- Remainder = Remainder - Divisor
- Remainder의 부호를 확인한다.
3-1. Remainder < 0 이라면, Divisor을 빼기 전으로 복원한 후, Quotient(몫)을 왼쪽으로 1bit 이동하고, Quotient의 LSB = 0
3-2. Remainder >= 0 이라면, 연산을 수행하지 않고, Quotient를 왼쪽으로 1bit 이동하고 Quotient의 LSB = 1 - Divisor을 오른쪽으로 1bit 이동한다.
Optimized Divider
- Remainer / Quotient를 왼쪽으로 1bit 이동한다.
- Remainder = Remainder - Divisor
- Remainder의 부호를 확인한다.
3-1. Remainder < 0 이라면, Divisor을 빼기 전으로 복원한다.
3-2. Remainder >= 0 이라면, 연산을 수행하지 않고, Quotient의 LSB = 1

