
Dictionary
list가 접근에서, linked list가 추가,삽입에 장점을 가지고 있다면, dictionary는 키(key)를 통해서 데이터를 찾아가는 방식으로 탐색에서 강점을 가지는 자료구조 형태이다.
Hash table (해시 테이블)
key와 value로 이루어진 자료구조로, key값을 해시함수로 해싱하여 해시테이블의 특정위치로 직접 액세스하도록 만든 방식.
해시함수
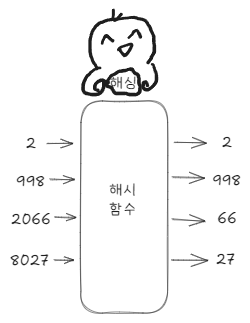
키 값을 해싱하여 고유한 인덱스를 만드는 함수이다. 인덱스가 중복되면 곤란하기 때문에, 반드시 하나의 키값을 해싱하는 경우 고유한 인덱스 값을 반환해야한다.
주의점
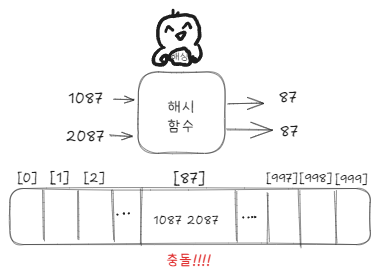
해시함수가 서로 다른 입력 값에 대해 동일한 해시테이블 주소, 인덱스를 반환하게 될 경우 동일한 인덱스에 2개 이상의 데이터가 들어가게 되는 문제가 발생한다. 하지만 모든 입력 값에 대해 고유한 해시 값을 만드는 것은 불가능하여 충돌은 피할 수 없기에, 이를 해결하기 위한 추가 조치가 필요하다.
충돌 해결 방안
-
체이닝
해시 충돌이 발생하면 연결리스트로 해당 인덱스의 데이터들을 연결하는 방식
장점 : 해시테이블의 자료 사용률에 따른 성능 저하가 적다.
단점 : 해시테이블 외 추가적인 저장공간이 필요하고, 삽입 삭제시 오버헤드가 발생하여 속도가 느려진다. -
개방 주소법
해시 충돌이 발생하면 다른 빈 공간에 데이터를 삽입하는 방식으로, 해시 충돌시 해시 테이블 내의 다른 빈 공간을 선정하여 저장한다.
장점 : 추가적인 저장공간이 필요하지 않고, 삽입 삭제시 오버헤드가 적어 속도가 느려지지 않는다.
단점 : 해시 테이블의 공간을 활용하기에 자료사용률에 따라 성능저하가 발생한다.
해시테이블의 효율
해시테이블은 공간 사용률이 높아짐에 따라 급격하게 성능저하가 발생한다. 따라서 70% 이상 사용을 하는 경우 재해싱 과정을 거쳐 확장을 진행하여 효율을 확보한다.
해시 테이블의 시간 복잡도는 접근을 제외한 나머지 항목에 대해 O(1)을 갖는다. 하지만 낮은 시간 복잡도로 해시테이블을 활용하는 것은 아니다. 사용률이 높아짐에 따라 효율이 떨어지는 특성상 여러 데이터를 추가하는 상황에는 어울리지 않기 때문이다.
Dictionary의 사용
static void Main1(string[] args)
{
Dictionary<string, Monster> monsterDic = new Dictionary<string, Monster>(10);
// 추가 : O(1)
monsterDic.Add("피카츄", new Monster("피카츄", 1));
monsterDic.Add("파이리", new Monster("파이리", 2));
// 키 값에 중복된 데이터가 들어가면 안된다.
monsterDic.Add("피카츄", new Monster("다른 피카츄", 5)); // 오류
// 제거 : O(1)
monsterDic.Remove("피카츄");
// 탐색 : O(1) - 있는지 없는지 불확실한 상황에서 사용
if (monsterDic.ContainsKey("파이리"))
{
monsterDic.Add("파이리",new Monster("파이리",2));
}
monsterDic.TryGetValue("파이리", out Monster monster);
// 인덱서를 통한 간략한 사용 - 키를 마치 인덱스처럼 사용이 가능하다.
// 탐색 : O(1) - 있는지 없는지 확실한 상황에서 사용
Monster find = monsterDic["파이리"];
// 인덱서를 통한 간략한 사용 - 키를 마치 인덱스처럼 사용이 가능하다.
// 추가 : O(1) - 이미 데이터가 있는 경우 신규 데이터로 변경된다.
monsterDic["피존투"] = new Monster("피존투", 6);
}Graph
데이터의 구조는 단순히 일직선 상으로만 표현되는 것이 아닌, 그물처럼 얽힌 구조도 존재한다. 이러한 데이터의 관계를 표현하기 위한 자료구조는 어떤 것이 있으며, 어떻게 구현해야하는지 알아보자.
비선형 자료구조
POE나 디아4에서는 거미줄 형태로 전개되어있는 스킬트리가 구현되어있는데, 이러한 형태의 데이터 관계를 나타낸 것이 비선형 자료구조라고 볼 수 있다.
그래프의 종류
- 방향성
- Directed Graph(단방향 그래프)
- Undirected Graph(양방향 그래프)
- 가중치
- Weighted Graph (가중치 그래프)
- Unweighted Graph (비가중치 그래프)
그래프의 구현 - vertex/edge
C#에서는 컬렉션으로 자료구조의 구현체를 제공했지만, 그래프는 쓰임과 활용에 따라 구조가 달라지기 때문에, 상황에 맞도록 구현하는 능력이 필요하다. 그렇다면 먼저 꼭짓점(vertex)과 모서리(edge)를 통해 구현하는 방식을 알아보자.
public class GraphNode<T>
{
public T vertex;
public T Vertex
{
get { return vertex; }
set { vertex = value; }
}
private List<GraphNode<T>> edges = new List<GraphNode<T>>();
public GraphNode(T vertex)
{
this.vertex = vertex;
}
public void AddEdge(GraphNode<T> node)
{
//단방향 연결
edges.Add(node);
//양방향 연결 (추가시)
//node.edges.Add(this);
}
public void RemoveEdge(GraphNode<T> node)
{
edges.Remove(node);
}
public bool IsConnect(GraphNode<T> node)
{
return edges.Contains(node);
}
}그래프의 구현 - matrix
그래프는 2차원 배열을 [출발점,도착점]으로 표현한 인접행렬로도 표현이 가능하다. 이 경우 인접 여부를 확인하는 과정이 빠르다는 장점이 있으나, 연결되어있지 않은 경우에도 메모리에 할당이 되어, 메모리 사용량이 많다는 단점을 가진다.
// 비가중치 그래프
bool[,] unWeightedGraph = new bool[8, 8];
unWeightedGraph[0, 3] = true;
unWeightedGraph[3, 0] = true;
// 가중치 그래프
int[,] weightedGraph = new int[8, 8];
weightedGraph[0, 3] = 3;
weightedGraph[3, 0] = 5;그래프의 구현 - List
matrix의 단점을 보완하기 위해 인접한 간선만을 List에 추가하여 양방향 비가중치 그래프를 표현하는 것이 가능하다. 이 경우 메모리 사용이 적다는 장점이 있지만, 인접 여부를 확인하기 위해서는 리스트 탐색이 필요하기에 조금 느리다는 단점을 가진다.
List<int>[] listGraph = new List<int>[8];
listGraph[0] = new List<int>() { 2, 3 };
listGraph[1] = new List<int>() { 3, 4, 5};
listGraph[2] = new List<int>() { 0, 3, 5};
listGraph[3] = new List<int>() { 0, 1, 2};
// 연결 추가
listGraph[0].Add(3);
listGraph[3].Add(0);
// 연결 제거
listGraph[1].Remove(3);
listGraph[3].Remove(1);
// 연결 여부 확인
bool isConected = listGraph[1].Contains(3);그래프의 구현 - class
Matrix와 List로 그래프를 구현하는 것을 class 생성하는 것으로도 진행할 수 있다. 추상클래스 선언과 함께 확장성을 고려하고, 자식 클래스에서 필수 메소드를 구현함으로써 단방향 비가중치 그래프를 구현해보자.
public abstract class Graph<T>
{
public abstract void AddEdge(int from, int to);
public abstract void RemoveEdge(int from, int to);
public abstract bool IsConnected(int from, int to);
}
public class MatrixGraph<T> : Graph<T>
{
private bool[,] data;
public MatrixGraph(int count)
{
data = new bool[count, count];
}
public override void AddEdge(int from, int to)
{
data[from, to] = true;
data[to, from] = true;
}
public override void RemoveEdge(int from, int to)
{
data[from, to] = false;
data[to, from] = false;
}
public override bool IsConnected(int from, int to)
{
return data[from, to];
}
}연결을 추가하는 AddEdge와 연결을 끊는 RemoveEdge, 연결을 확인하는 IsConnected를 구현하여 그래프의 기능을 할 수 있도록 한다.
Assignment
양방향 가중치 그래프를 구현하여라.
public class assignment
{
public class MatrixGraph
{
public int[,] matrix;
public int[,] Matrix
{
get { return matrix; }
set { matrix = value; }
}
public void Init()
{
matrix = new int[8, 8];
}
public MatrixGraph() => Init();
public void Add(int from, int to, int weight)
{
matrix[from, to] = weight;
}
public void Remove(int from, int to)
{
matrix[from, to] = -1;
}
public void Print()
{
for (int j = 0; j < 8; j++)
{
Console.Write($"{j}노드 : ");
for (int i = 0; i < 8; i++)
{
if (matrix[j, i] != 0 && matrix[j, i] != -1)
Console.Write($"- {i}노드, 가중치 {matrix[j, i]} ");
else continue;
}
Console.WriteLine();
}
}
public void Clear() => Init();
}
}Add함수를 통해 두 노드 간의 가중치를 matrix에 저장할 수 있도록 하고, Remove로 다시 없애도록, Print로 연관이 있는 노드 간의 가중치가 나타나도록 구현하였다.
