
A* Algorithm
Unity 3D는 NavMesh를 사용하여 간편히 길찾기 기능을 구현할 수 있었으나, 2D의 경우 유니티에서 직접적으로 지원하는 NavMesh 툴이 없기에 따로 구현할 필요가 있다.
길찾기 알고리즘은 Astar 알고리즘으로 구현할 수 있는데, BFS에서 파생된 길찾기 알고리즘 중 하나로, 다양한 분야에서 자주 사용되는 알고리즘이다. 자세한 개념은 A* 알고리즘 에 정리해놓았으니 참고하면 된다.
이번에는 A* 알고리즘을 활용하여 2D 타일 맵 상에서의 길찾기 기능을 구현해보자.
2D 타일맵 A* 알고리즘 시각적 표현
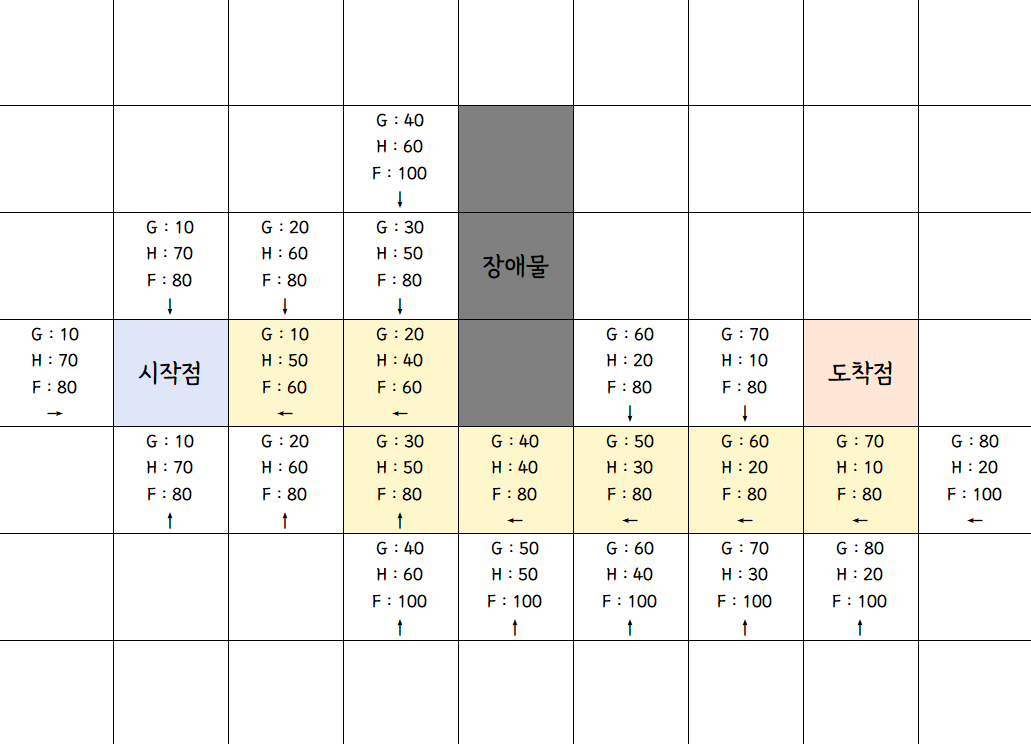
위의 사진은 2D 타일맵 상에서의 A* 알고리즘을 시각적으로 표현한 것이다.
- G : 현재까지 비용
- H : 목표까지 비용
- F : 총 비용 (G+H)
- 화살표 : 부모 노드 표현
다음 경로를 결정하는 기준은 탐색한 정점 중 F값이 최소인 정점이며, 탐색한 정점이 도착점인 경우 탐색을 멈추고 저장한 부모 노드를 추적하여 최종 경로를 출력한다.
A* 알고리즘 스크립트
Node
먼저 정점의 정보를 저장하기 위한 Node 클래스를 생성할 필요가 있다. 이전에 구현했던 것과는 달리 2D World 좌표를 가져와 저장할 수 있도록 Vector2Int 프로퍼티를 내부에 구현해둔다.
public class Node
{
// F : 총 비용
public float F => G + H;
// G : 현재까지 비용
public float G;
// H : 목표까지 비용
public float H;
// 부모 노드 : 자신을 탐색한 노드, 경로를 출력하기 위해 필요
public Node Parent;
// 현재 노드 위치
public Vector2Int Position;
public Node(Vector2Int position)
{
// 생성시 위치 설정
Position = position;
// 아직 방문하지 않았다는 의미로 최댓값 부여
G = float.MaxValue;
}
}Direction
대각선 이동이 가능하도록 설정했기에 현재 정점으로부터 8방향으로 탐색이 가능하도록 각 방향의 정보를 저장하기위한 Vector2Int 배열을 생성해둔다.
private static readonly Vector2Int[] Directions =
{
new Vector2Int(1, 0), // 오른쪽
new Vector2Int(-1, 0), // 왼쪽
new Vector2Int(0, 1), // 위
new Vector2Int(0, -1), // 아래
new Vector2Int(1, 1), // 오른쪽 위
new Vector2Int(-1, 1), // 왼쪽 위
new Vector2Int(1, -1), // 오른쪽 아래
new Vector2Int(-1, -1) // 왼쪽 아래
};Heuristic
대각선 이동이 가능하기에 휴리스틱 함수는 유클리드 거리를 사용하여 계산한다. 참고로 대각선 이동이 불가능한 경우 맨해튼 거리(Mathf.Abs(a.x - b.x) + Mathf.Abs(a.y - b.y))를 사용하면 된다.
private static float Heuristic(Vector2Int a, Vector2Int b)
{
// return Mathf.Round((Mathf.Pow((b.x - a.x), 2) + Mathf.Pow((b.y - a.y), 2)));
return Vector2.Distance(a, b);
}IsValid
매개변수로 입력된 position으로 이동 가능한지 여부를 판단하는 메서드. 매개변수에 입력된 map은 해당 좌표의 타일이 이동가능한지 여부에 대한 정보가 들어있는 bool타입 배열이다.
private static bool IsValid(bool[,] map, Vector2Int pos)
{
// 1. x의 값이 0보다 크거나 같고, 너비보다 작음
// 2. y의 값은 0보다 크거나 같고, 높이보다 작음
// => mapping되지 않은 타일은 모두 이동 불가 처리
// 3. 해당 x,y가 장애물이 아닐 경우 true
int w = map.GetLength(0);
int h = map.GetLength(1);
return (pos.x >= 0 && pos.x < w) && (pos.y >= 0 && pos.y < h) && map[pos.x, pos.y];
}ConvertToMap
실제 mapping 정보를 IsValid에 사용될 수 있도록 bool타입 배열로 바꿔주는 메서드이다. wallPositions에는 장애물, 벽 등의 갈 수 없는 타일의 위치 정보가 기록되어있다.
public static bool[,] ConvertToMap(List<Vector3Int> wallPositions, int width, int height)
{
bool[,] map = new bool [width, height]; // 반환에 사용하기 위한 bool타입 배열
for (int x = 0; x < width; x++) // 너비만큼 반복
{
for (int y = 0; y < height; y++) // 높이만큼 반복
{
// 해당 위치가
Vector2Int pos = new Vector2Int(x,y);
// wallPositions에 있으면 false 없으면 true
map[x, y] = !wallPositions.Contains((Vector3Int)pos);
}
}
return map;
}BuildPath
탐색을 끝낸 최단 경로를 출력해주는 메서드. 경로에 포함될 정점들의 위치를 저장할 배열을 선언하고, 마지막 노드부터 상위 탐색 노드를 타고 올라가며 탐색한 정점들의 정보를 저장한다. 마지막에 배열의 순서만 바꿔서 출력하면 시작점부터 도착점까지의 경로가 출력된다.
private static List<Vector2Int> BuildPath(Node endNode)
{
List<Vector2Int> pathList = new List<Vector2Int>();
// 매개 변수로 받은 마지막 노드
Node pathNode = endNode;
// 경로 찾는데에 사용된 노드가 null이 되면 종료
while (pathNode != null)
{
// 경로 노드의 위치 추가
pathList.Add(pathNode.Position);
// 추가 했으면, 경로 노드를 해당 노드의 부모 노드로 변경
pathNode = pathNode.Parent;
}
pathList.Reverse();
return pathList;
}A* Algorithm
사전 준비를 모두 마쳤다면 본격적으로 A* 알고리즘을 구현해보자. 우선 의사 코드로 로직을 작성하면 다음과 같다.
-
자료 구조 초기화
1)openList: 탐색할 가치가 있는 노드들을 저장할 수 있는 리스트
2)closedList: 이미 탐색을 마친 노드들의 위치를 가지고 있을 리스트
3)allNodes: 위치(Vector2Int) 기반으로 생성된 모든 노드를 저장하는 자료 구조 -
시작점에서 시작 노드 생성 및 openList, allNodes 추가
-
탐색 반복(goal 위치에 도달할 때까지)
1) openList에 노드가 들어있고, 여기에서 F값(같을 경우 H값)이 낮은대로 정렬2) 가장 첫번째 노드 (= F값과 H값이 최소인 노드)를 현재 노드로 설정
3) 해당 원소의 위치를 closedList에 추가
- 현재 선택 노드의 위치가 도착점과 같으면 최단 경로를 반환
4) Directions을 이용하여 자신을 중심으로 8방향 판단.
- 다음으로 진행할 방향이 이동할 수 있는 위치인지 => 장애물인지 아닌지 판단해야함. 맵 규격에 맞는지.
- 대각선 이동이 존재할 때, 인접한 수직, 수평방향으로 벽이 있지 않은지도 판단해야함.
5) 이동했으므로, 이동거리를 계산 (수직, 수평 = 1, 대각선 1.4) => G
6) 휴리스틱을 계산 => H, F(G + H)값 도출- 만약 해당 위치에 Node가 없다면 생성
7) 이동거리가 기존의 이동거리보다 작다면 G에 할당해주어야함 => H값, parent를 할당해준다.
8) openList에 해당 노드가 없다면 추가
public static List<Vector2Int> FindPath(bool[,] map, Vector2Int start, Vector2Int goal)
{
// 1. 자료 구조 초기화
List<Node> openList = new List<Node>();
List<Vector2Int> closedList = new List<Vector2Int>();
Dictionary<Vector2Int, Node> allNodes = new Dictionary<Vector2Int, Node>();
// 2. 시작점에서 시작 노드 생성 및 openList, allNodes 추가
Node startNode = new Node(start) { G = 0, H = Heuristic(start, goal) };
openList.Add(startNode);
allNodes[start] = startNode;
// 3. 탐색 반복(더 이상 탐색할 위치가 없을 때까지)
while (openList.Count > 0)
{
// 3-1) openList 순서 정렬
// PriorityQueue를 구현한 경우 해당 과정 필요x
openList.Sort((a, b) =>
{
// F값 기준 오름차순으로 정렬
int fComparison = a.F.CompareTo(b.F);
// 만약 F값이 같으면
if (fComparison == 0)
{
// H값 기준 오름차순으로 정렬
// => 남은 경로(H)가 작아야 최단 경로일 가능성 ↑
return a.H.CompareTo(b.H);
}
return fComparison;
}
);
// 3-2) openList의 첫 번째 원소(F가 제일 작은 정점)를 현재 노드로 설정
Node curNode = openList[0];
// 3-3) 탐색할 예정이므로 openList에서 제거 및 closedList에 추가
openList.RemoveAt(0);
closedList.Add(curNode.Position);
// 현재 노드(정점)이 도착점이라면 해당 노드부터 경로를 반환하고 반복문 종료
if (curNode.Position == goal)
{
return BuildPath(curNode);
}
// 3-4) Directions을 이용하여 자신을 중심으로 8방향 판단
foreach (Vector2Int dir in Directions)
{
// 현재 위치 기준 8방향 위치를 저장
Vector2Int nextPos = curNode.Position + dir;
// 해당 위치가 장애물이거나, closedList에 포함되어 있으면 스킵
if (!IsValid(map, nextPos) || closedList.Contains(nextPos))
{
continue;
}
// 대각선 이동일 경우(가로, 세로 이동이 존재하는 경우)
if (Mathf.Abs(dir.x) == 1 && Mathf.Abs(dir.y) == 1)
{
Vector2Int horizontal = new Vector2Int(curNode.Position.x + dir.x, curNode.Position.y);
Vector2Int vertical = new Vector2Int(curNode.Position.x, curNode.Position.y + dir.y);
// 가로, 세로 이동이 가능한 지 확인 후, 둘 다 불가능하면 스킵
if (!IsValid(map, horizontal) && !IsValid(map, vertical))
{
continue;
}
}
// 3-5) 이동거리 변화량(delta G) 계산
float deltaG = (dir.x == 0 || dir.y == 0) ? 1f : 1.4f;
// 3-6) 현재의 G값에 이동거리 변화량을 더한 값으로 갱신
float newG = curNode.G + deltaG;
float newH = Heuristic(nextPos, goal);
// Node로 생성되어있지 않은 경우
if (!allNodes.TryGetValue(nextPos, out Node nextNode))
{
// Node 신규 생성 및 allNodes에 추가
nextNode = new Node(nextPos) { H = newH };
allNodes[nextPos] = nextNode;
}
// 3-7) 만약 현재 새로운 G 값이 nextNode의 값보다 작다면
// => 최초 생성 Node G값은 Max
if (newG < nextNode.G)
{
// G값 갱신
nextNode.G = newG;
// 상위 탐색 노드 갱신
nextNode.Parent = curNode;
// 3-8) openList에 없으면 추가
if (!openList.Contains(nextNode))
{
openList.Add(nextNode);
}
}
}
}
// while 반복문 종료 이후에도 경로를 반환하지 못 한 경우 null을 반환
return null;
}