구간 합

구간 합은 합 배열을 이용하여 시간 복잡도를 더 줄이기 위해 사용하는 특수한 목적의 알고리즘이다.

합 배열S 정의

합 배열 S는 배열 A의 값을 빠르게 계산하기 위해 미리 부분합을 저장한 배열이다. 즉, 배열 S의 각 원소는 배열 A의 0번째부터 해당 인덱스까지의 누적합을 나타낸다.

S[i] = A[0] + A[1] + A[2] + ... + A[i-1] + A[i]

합 배열을 사용해야 하는 이유

합 배열을 미리 구해 놓으면 기존 배열의 일정 범위의 합을 구하는 시간 복잡도가 O(N)에서 O(1)로 감소한다.

# 배열 A
A = [2, 4, 6, 8, 10]

# 합 배열 S 구하기
S[0] = A[0] = 2
S[1] = S[0] + A[1] = 2 + 4 = 6
S[2] = S[1] + A[2] = 6 + 6 = 12
S[3] = S[2] + A[3] = 12 + 8 = 20
S[4] = S[3] + A[4] = 20 + 10 = 30

# 합 배열 S
S = [2, 6, 12, 20, 30]

# 특정 범위의 합 구하기 [1, 3]
# 직접 계산 
A[1] + A[2] + A[3] = 4 + 6 + 8 = 18
# 합 배열로 계산 
S[3] - S[0] = 20 - 2 = 18

합 배열 S를 만드는 공식

S[i] = S[i-1] + A[i]

구간 합을 구하는 공식

S[j] - S[i-1]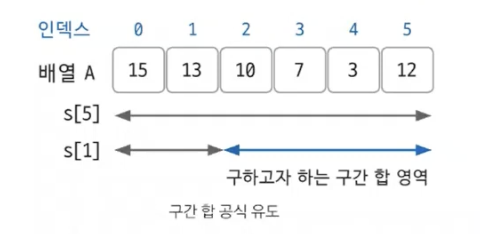

배열 A의 A[2]부터 A[5]까지의 구간 합을 합 배열을 통해 구하는 과정은 아래와 같다.

S[5] = A[0] + A[1] + A[2] + A[3] + A[4] + A[5]
S[1] = A[0] + A[1]
S[5] - S[1] = A[2] + A[3] + A[4] + A[5]

구간 합 구하기 5 : 11660

문제

예제

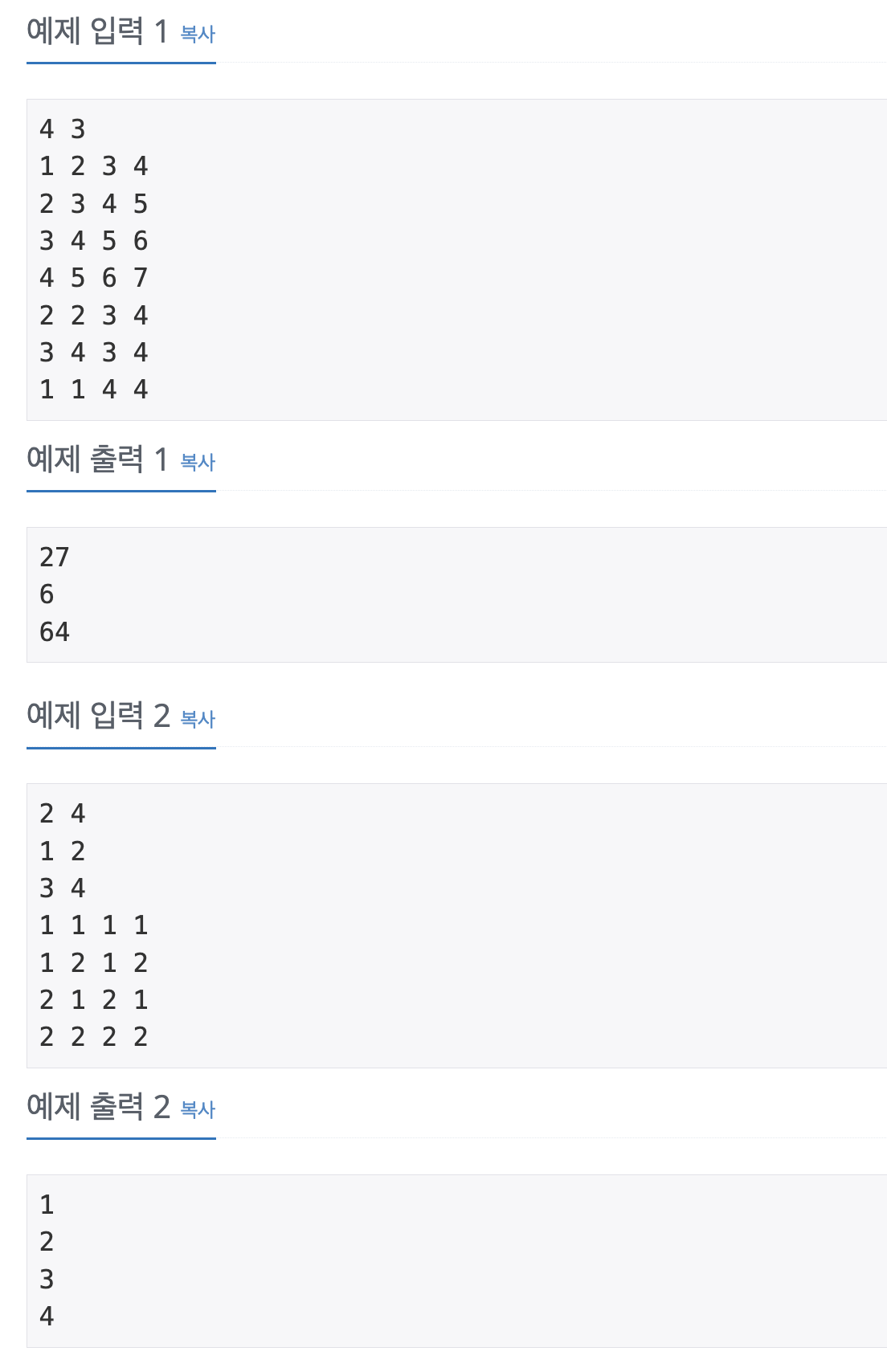
풀이

질의의 개수가 100,000이므로 질의마다 합을 구하면 안되고, 구간 합 배열을 이용해서 문제를 풀어야 한다. 구간 합 배열이 1차원에서 2차원으로 확장된 것으로 생각하여 구간 합 배열을 어떻게 구성할지 고민하는 것이 문제의 핵심이다.

import sys
input = sys.stdin.readline
n, m = map(int, input().split())
a = [[0] * (n+1)]
d = [[0]*(n+1) for _ in range(n+1)]

for i in range(n):
    a_row = [0] + [int(x) for x in input().split()]
    a.append(a_row)

for i in range(1, n+1):
    for j in range(1, n+1):
        d[i][j] = d[i][j-1] + d[i-1][j] -d[i-1][j-1] + a[i][j]
        
for _ in range(m):
    x1, y1, x2, y2 = map(int, input().split())
    result = d[x2][y2] -d[x1-1][y2] -d[x2][y1-1] + d[x1-1][y1-1]
    print(result)

끄적끄적

이 문제도 질의의 개수가 많아서 그런지 print()를 사용하면 시간초과 오류가 나온다.