브루트 포스

2798: 블랙잭

문제

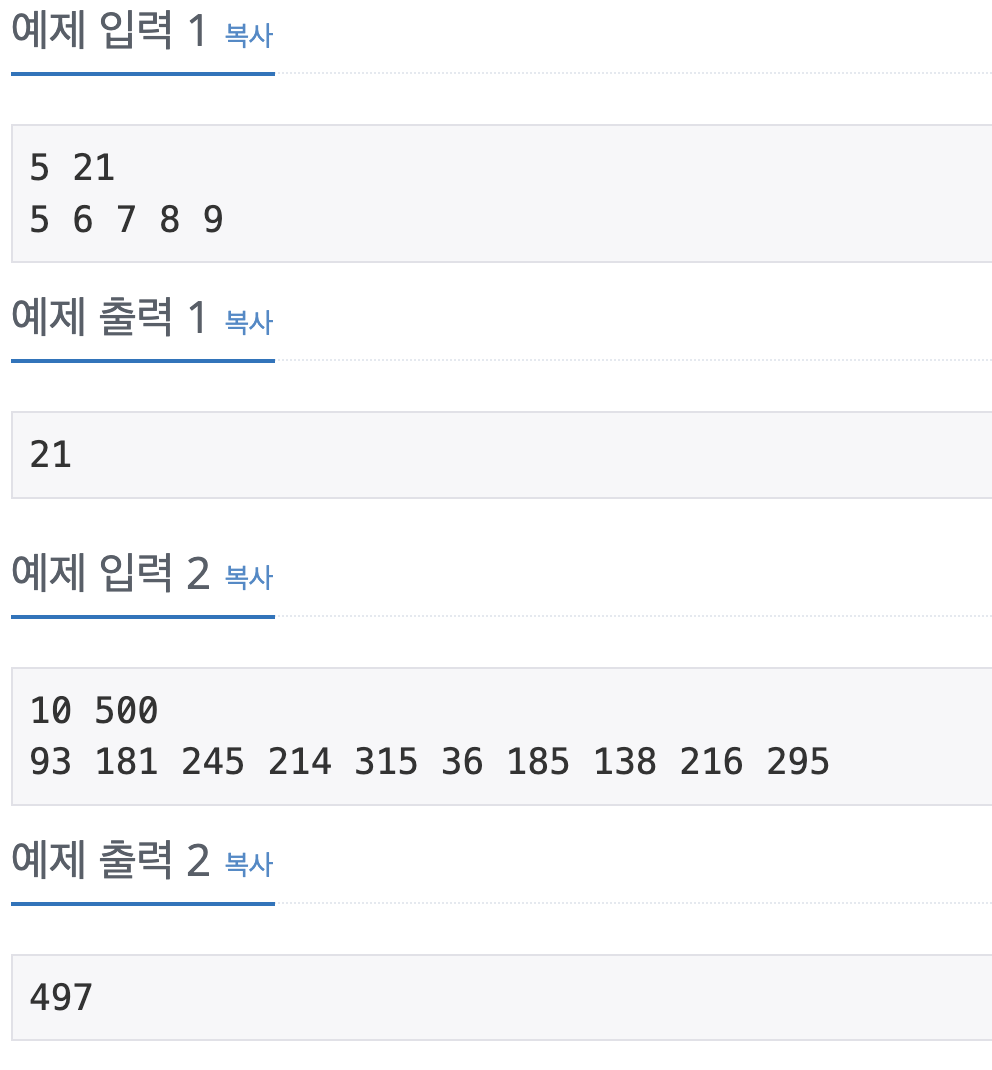
예제

나의 풀이

조합을 이용하면 간단하게 풀이할 수 있다.

from itertools import combinations
n, m = map(int, input().split())
cards = list(map(int, input().split()))

max_com = 0
com_cards = list(combinations(cards,3))
for i in com_cards:
    if sum(i) <= m and sum(i) > max_com:
        max_com = sum(i)
        
print(max_com)

다른 풀이

my_max = 0
for i in range(N - 2):
    for j in range(i + 1, N - 1):
        for k in range(j + 1, N):
            my_sum = arr[i] + arr[j] + arr[k]
            if my_max < my_sum <= M:
                my_max = my_sum 
print(my_max)

⭐️1018: 체스판 다시 칠하기

문제

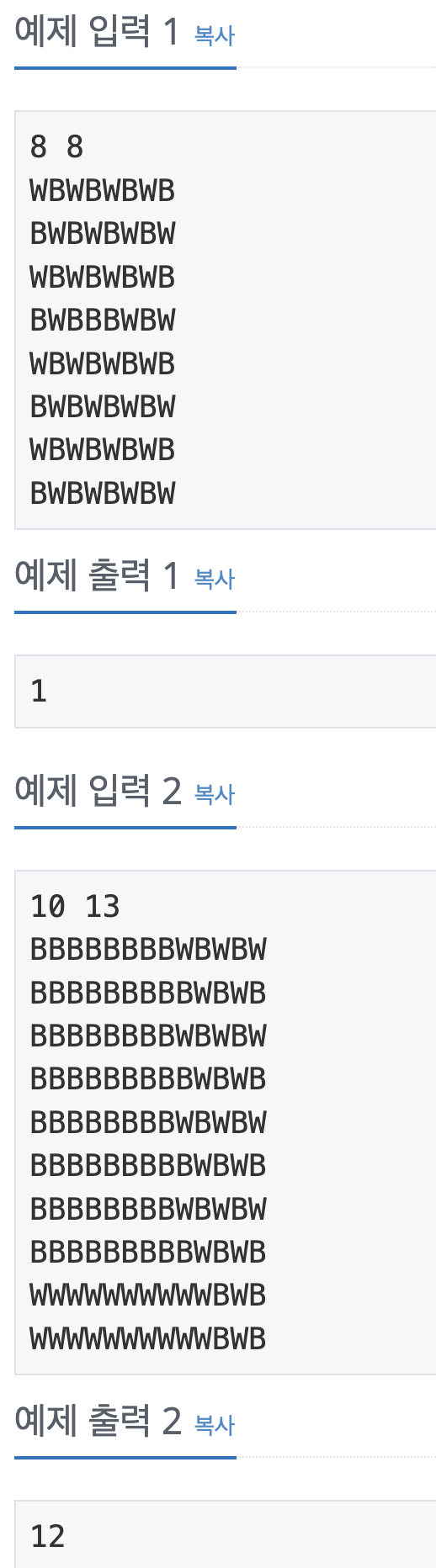
예제

풀이

다시 풀어봐야 겠다.

n,m = map(int, input().split())
board = []
for _ in range(n):
    color = input()
    board.append(color)

cnt = []
for a in range(n-7):
    for b in range(m-7):
        w_index = 0
        b_index = 0
        for i in range(a, a+8):
            for j in range(b, b+8):
                if (i+j)%2 == 0:
                    if board[i][j] != "W":
                        w_index+=1
                    else:
                        b_index+=1
                else:
                    if board[i][j] != "W":
                        b_index+=1
                    else:
                        w_index+=1
        cnt.append(w_index)
        cnt.append(b_index)
print(min(cnt))

2839: 설탕 배달

문제

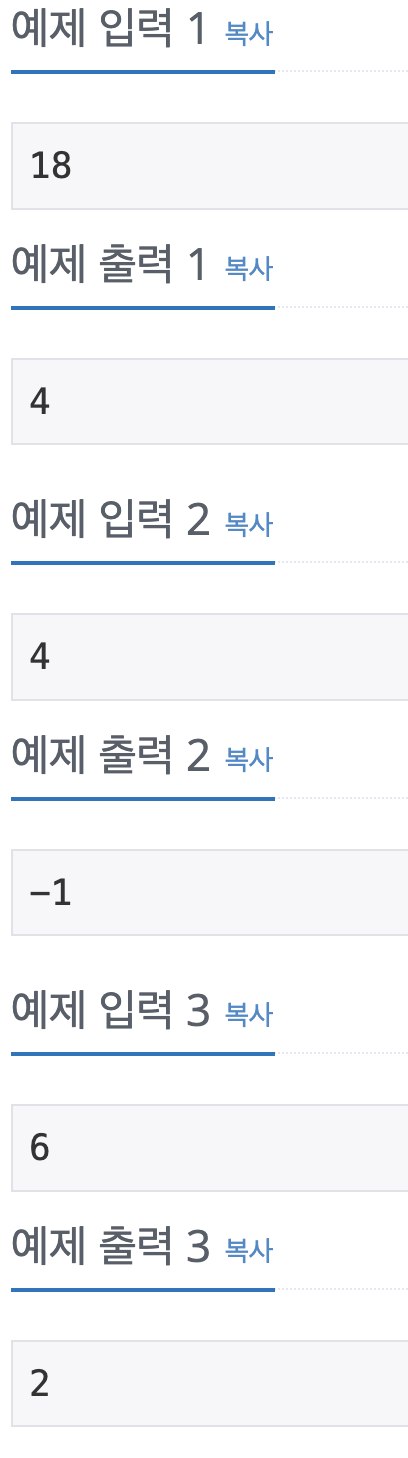
예제

나의 풀이

최대한 5kg 봉지를 먼저 사용하고 남은 무게를 3kg으로 채우는 방식으로 풀이했다.

n = int(input())

count = 0
while n >= 0:
    if n % 5 == 0:  # 5kg 봉지로 나누어 떨어지는 경우
        count += n // 5  # 5kg 봉지 개수 추가
        print(count)
        break
    n -= 3  # 5kg으로 나눠지지 않으면 3kg을 하나 사용
    count += 1
else:
    print(-1)  # 정확한 무게를 만들 수 없는 경우

다른 풀이

1. Brute Force(완전 탐색법)
   5kg 봉지의 개수를 줄여가면서 3kg 봉지로 나누어 떨어지는지 확인하는 방법이다.

n = int(input())

# 5kg 봉지를 최대한 많이 사용
for i in range(n // 5, -1, -1):  # 가장 큰 5kg 봉지 개수부터 시작
    remain = n - (5 * i)  # 5kg을 최대한 사용한 후 남은 무게
    if remain % 3 == 0:  # 남은 무게가 3kg으로 나누어 떨어지는 경우
        print(i + (remain // 3))  # 5kg 개수 + 3kg 개수 출력
        break
else:
    print(-1)  # 정확한 무게를 만들 수 없는 경우

2. DP 풀이방법(동적 계획법)
   메모이제이션 활용 방식으로 작은 문제를 풀면서 결과를 저장하여 큰 문제를 빠르게 해결하는 방식이다. 더 다양한 무게 조건이 있는 경우 DP를 활용하여 풀면 좋을 것 같다.

n = int(input())

dp = [-1] * (n + 1)  # dp[i] = i kg을 만들 수 있는 최소 봉지 수 (불가능하면 -1)
if n >= 3:
    dp[3] = 1
if n >= 5:
    dp[5] = 1

for i in range(6, n + 1):  # 3kg, 5kg을 이용해 dp 갱신
    if dp[i - 3] != -1:
        dp[i] = dp[i - 3] + 1
    if dp[i - 5] != -1:
        dp[i] = min(dp[i], dp[i - 5] + 1) if dp[i] != -1 else dp[i - 5] + 1

print(dp[n])