01. Tree
🔨 1. Tree의 정의!
- 자료구조 Tree는 나무를 뒤집어놓은 모습을 가진다.
- 단반향 그래프 구조로 하나의 뿌리로부터 가지가 사방으로 뻗은 형태이다.
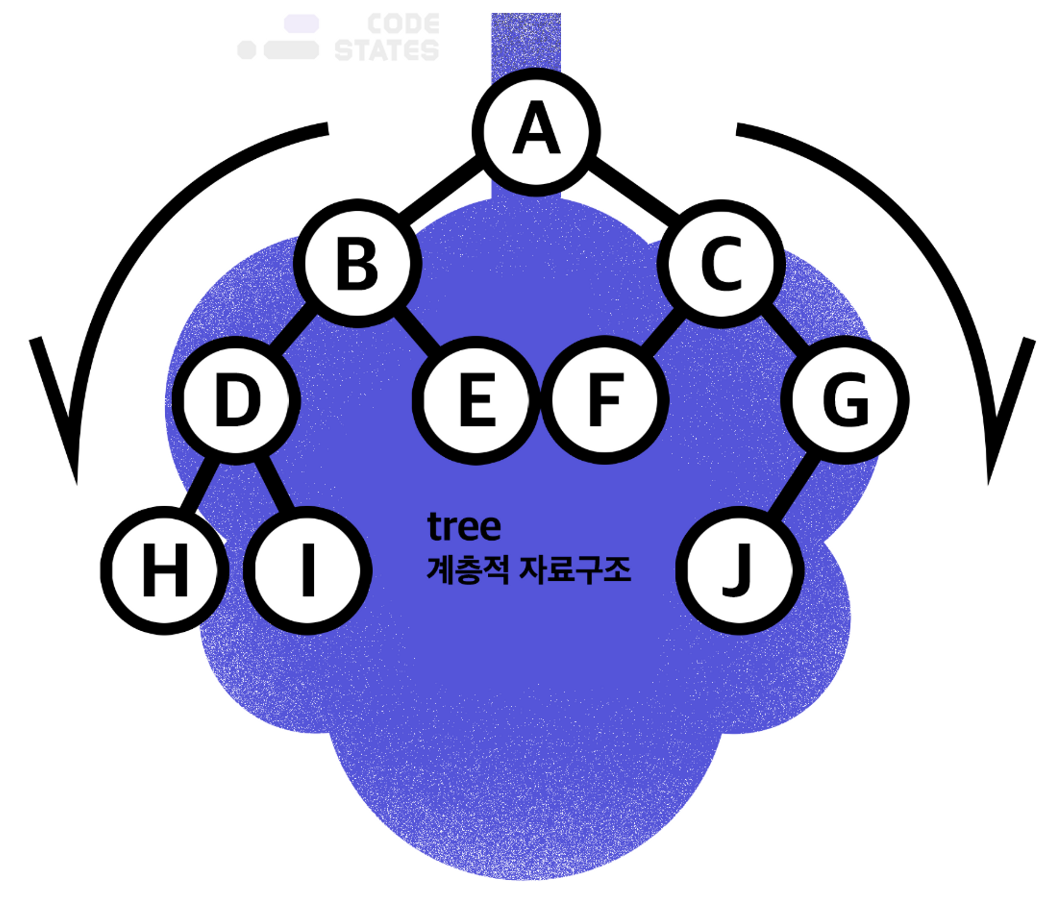
- 데이터가 바로 아래에 있는 하나 이상의 데이터에 →
한 개의 경로와 하나의 방향으로만 연결된 계층 자료구조이다.
- 선형구조 : 데이터를 순차적으로 나열
- 비선형구조 : 하나의 데이터 아래에 여러 개의 데이터가 존재 - 트리구조는 계층적으로 표현되고, 아래로만 뻗어나가기 때문에 사이클이 없다.
- 사이클이란 시작 노드에서 출발해 → 다른 노드를 거쳐 → 다시 시작 노드로 돌아올 수 있는 구조를 말하며, 이를 사이클이 존재한다고 한다.
- 따라서 트리는 사이클이 없는 하나의 연결 그래프(Connected Graph)이다.
🔨 2. Tree의 구조
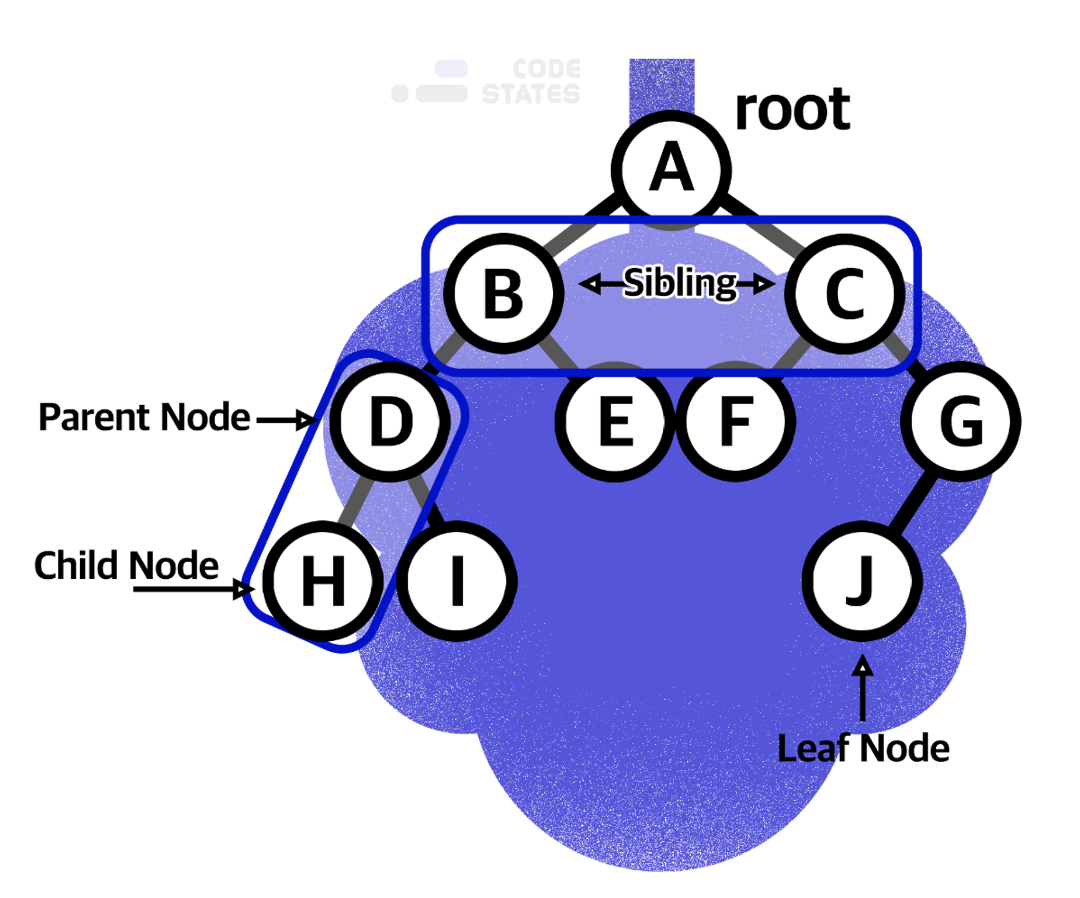
루트(Root)
하나의 꼭짓점 데이터를 시작으로 → 여러 개의 데이터를 간선(edge)으로 연결한다.
노드(Node)
각 데이터를 노드(Node)라고 하며,
두 개의 노드가 상하계층으로 연결되면 → 부모/자식 관계를 가진다.
A : B와 C의 부모노드(Parent Node)
B, C : A의 자식 노드(Child Node)이다.
...
J : 자식이 없는 노드로, 리프 노드(Leaf Node)라고 한다.🔨 3. Tree의 특징
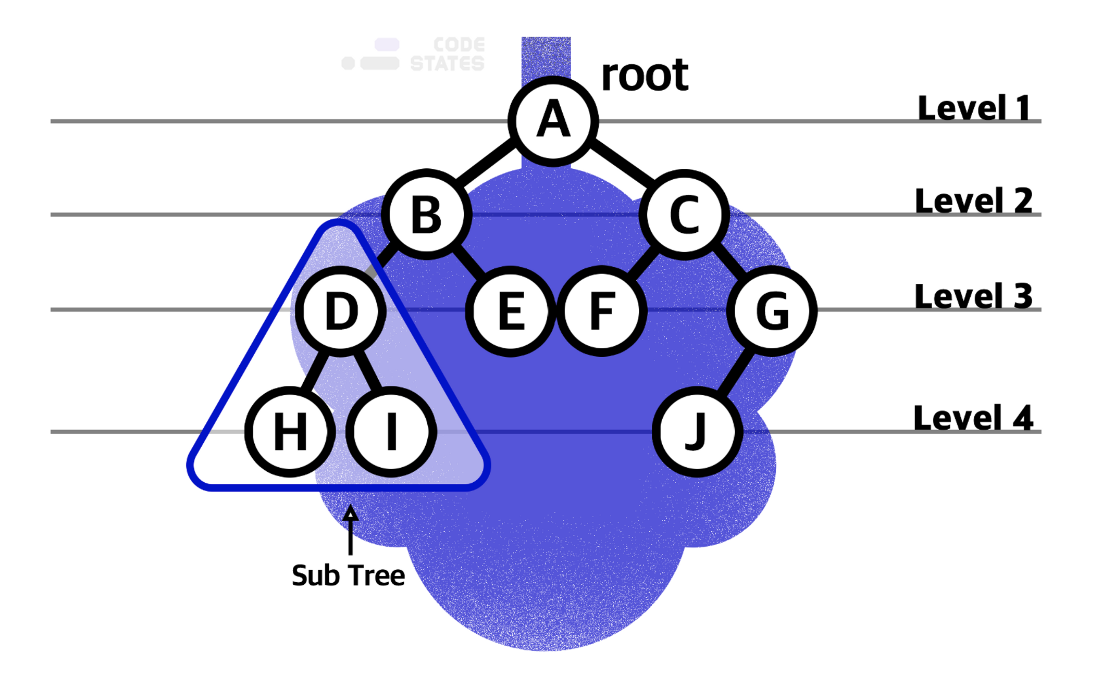
깊이(depth)
- 루트로부터 하위계층의 특정 노드까지의 깊이를 표현한다.
- 루트 노드의 깊이는 0이다.
- 루트 A의 depth : 0
- B, C의 depth : 1
- D, E, F, G의 depth : 2
- H, I, J의 depth : 3레벨(Level)
- 같은 깊이를 가진 노드를 묶어 레벨로 표현한다.
- 같은 레벨에 나란히 있는 노드를 형제 노드(Sibling Node)라고 한다.
- 루트 A의 level : 1
- B, C의 level : 2 --> 형제 노드
- D, E, F, G의 level : 3 --> 형제 노드
- H, I, J의 level : 4 --> 형제 노드높이(Height)
- 리프 노드를 기준으로 루트까지의 높이를 표현한다.
- 각 리프 노드의 높이는 0으로 놓는다.
- H, I, E, F, J의 높이 : 0
- D, G의 높이 : 1
- B, C의 높이 : 2 --> B : D의 height + 1 / C : G의 height + 1
- 루트 A의 높이 : 3서브트리(Sub tree)
- 큰 트리 내부에서, 트리 구조를 갖춘 작은 트리를 → 서브트리라고 한다.
* 서브트리
- D, H, I
- B, D, E
- C, F, G, J✏️ 용어정리
- 노드(Node) : 트리 구조를 이루는 모든 개별 데이터
- 루트(Root) : 트리 구조의 시작점이 되는 노드
- 부모 노드(Parent node) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 가까운 노드
- 자식 노드(Child node) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 먼 노드
- 리프(Leaf) : 트리 구조의 끝 지점이고, 자식 노드가 없는 노드
🔨 4. Tree의 실사용 예제
- 가장 대표적인 예제는 컴퓨터의 디렉토리 구조이다.
02. Binary Search Tree
트리 구조는 편리한 구조를 전시하고 + 효율적인 탐색을 위해 사용한다.
효율적인 탐색을 위한 트리구조 :이진 트리(binary tree),이진 탐색 트리(binary search tree)
🔨 1. 이진 트리(Binary tree)
- 자식 노드가 최대 두 개 인 노드들로 구성된 트리로, 두개의 자식 노드는 왼쪽 자식 노드와 오른쪽 자식 노드로 나뉜다.
- 자료의 삽입, 삭제 방법에 따라 종류가 구분된다.
정 이진 트리(Full binary tree)
- 각 노드는 0개 or 2개의 자식노드를 갖는다.
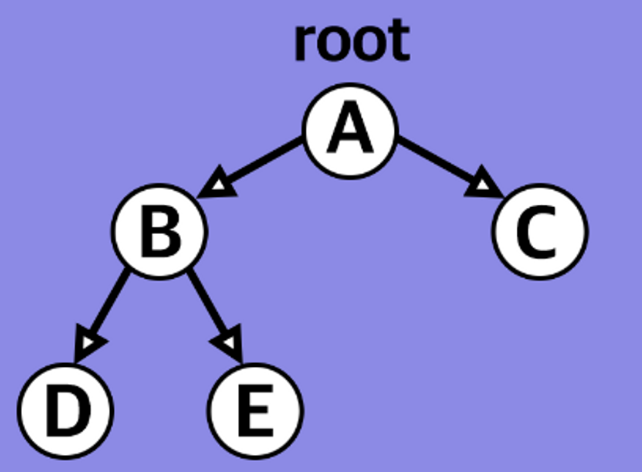
완전 이진 트리(Complete binary tree)
- 마지막 레벨을 제외한 모든 노드가 있고
- 마지막 레벨의 노드 중 왼쪽 노드는 반드시 있어야 한다.
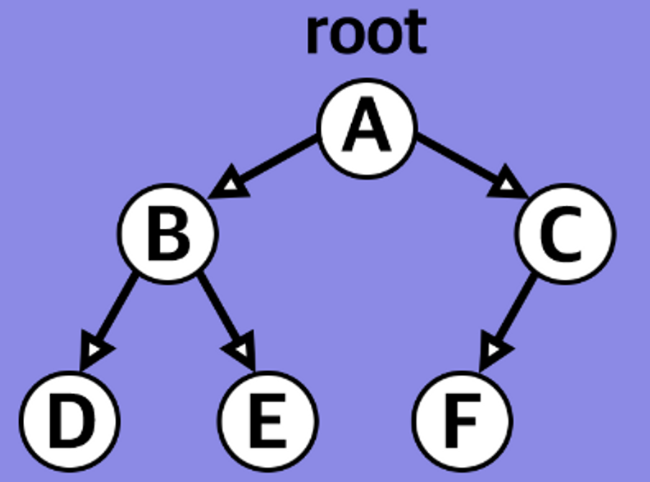
포화 이진 트리(Perfect binary tree)
**정 이진 트리**면서**완전 이진 트리**
- 모든 리트 노드의 레벨이 동일하고
- 모든 레벨이 가득 채워 있어야 한다.
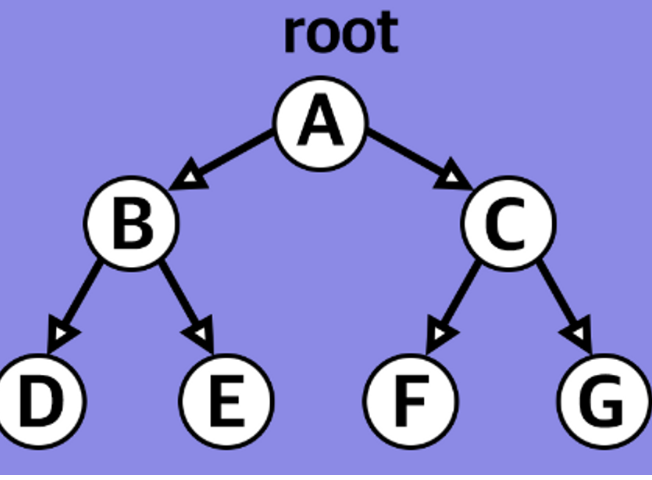
🔨 2. 이진 탐색 트리(Binary Search Tree)
- 이진 탐색 트리는
이진 탐색(binary search)과연결 리스트(linked list)를 결합한 이진트리 를 말한다. - 이진 탐색의 효율적인 탐색 능력을 유지하고 && 빈번한 자료 입력과 삭제가 가능하겠금 고안되었다.
- 각 노드엔 중복되지 않은 키(key)가 있다.
- ⬅️ 루트 노드의 왼쪽 서브 트리 : 해당 노드의 키보다 작은 키를 갖는다.
- ➡️ 루트 노드의 오른쪽 서브 트리 : 해당 노드의 키보다 큰 키를 갖는다.
- 좌우 서브트리도 모두 이진 탐색 트리여야 한다.
⇒ 즉 모든 왼쪽 자식의 값이 루트나 부모보다 작고, 모든 오른쪽 자식의 값은 루트나 부모보다 큰 값을 가진다.
🔎 이진 탐색 트리의 탐색 방법- 찾고자 하는 값과 루트 노트의 키와 비교한다. 만약 찾고자 하는 값이면 탐색을 종료한다.
- 찾고자 하는 값이 루트 노트의 값보다 작다면 왼쪽 서브트리로, 크다면 오른쪽 서브 트리로 탐색을 진행한다.
→ 만약 트리 안에 찾고자 하는 값이 없더라도 → 최대 높이(h)번의 연산 및 탐색이 진행된다.
03. 트리 순회Tree Traversal
- 특정 목적을 위해 트리의 모든 노드를 한 번씩 방문하는 것을 트리 순회라고 한다.
- 트리 구조에서 노드를 조회하는 순서는 항상 왼쪽 → 오른쪽이다.
- 트리 순회의 방법으론 전위 순회, 중위 순회, 후위 순회가 있다.
🔨 1. 전위 순회(Preorder Traverse)
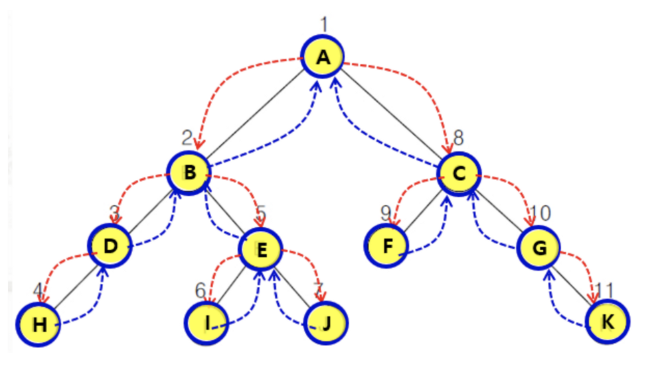
- 루트부터 순회한다.
1. 루트에서 시작해
2. 왼쪽 노드들을 순차적으로 둘러본 후,
왼쪽 노드 탐색이 끝나면
3. 오른쪽 노드들을 순차적으로 탐색한다.
-> 즉 부모 노드가 제일 먼저 방문되는 순회 방식이고
-> 전위 순회는 주로 부모 노드가 먼저 생성되어야 하는
트리를 복사할 때 사용한다.🔨 2. 중위 순회(inorder Traverse)
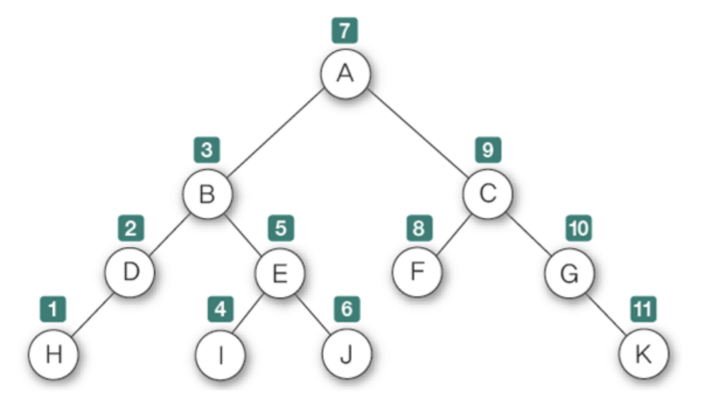
- 루트를 가운데 두고 순회한다.
1. 맨 왼쪽 끝에 있는 노드부터 순회하여
2. 루트를 기준으로 왼쪽 노드의 순회가 끝나면
3. 루트를 순회하고
4. 오른쪽에 있는 노드로 이동해 탐색한다.
-> 맨 오른쪽 자식 노드가 마지막이다.
-> 부모 노드가 서브트리의 방문 중간에 방문되는 순회 방식
-> 이진 탐색 트리의 오름차순으로 값을 가져올 때 사용한다.🔨 3. 후위 순회(Postorder Traverse)
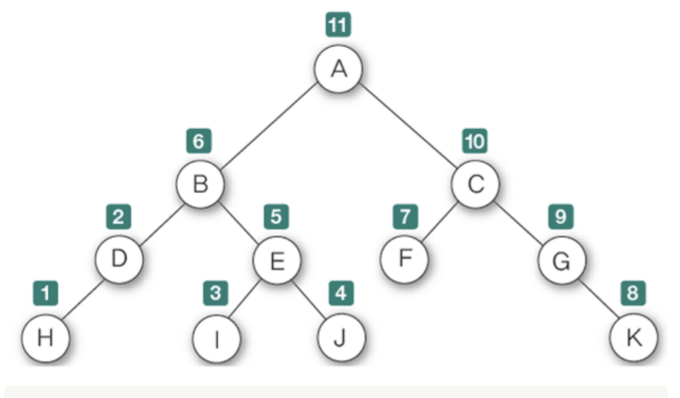
- 루트를 마지막으로 순회한다.
1. 맨 왼족 끝에 있는 노드부터 순회하여
2. 루트를 거치지 않고 -> 오른쪽으로 이동해 순회한 후
3. 제일 마지막에 루트를 방문한다.
-> 트리를 삭제할 때 사용한다.
because, 자식노드가 먼저 삭제되어야 상위 노드를 삭제할 수 있기 떄문이다.❓순회 방식을 나누는 이유
이진 트리 탐색의 경우 -> 탐색은 간단하지만 순회 방법이 조금 복잡하다.
- 일정한 조건에 의해 설계된 트리 구조는 -> 자식 노드에 대한 조건이 명확하다면 원하는 값을 쉽게 찾아낼 수 있지만,
트리 구조 전체를 탐색할 때는 값을 찾기 까다롭거나 오랜시간이 걸릴 수 있다.
-> 따라서 모든 노드를 방문하기 위해서는
1. 일정한 조건이 필요하고
2. 트리구조를 유지보수하거나 특정 목적을 위해서도 순회 방법에 대한 정의는 필수적이다.