↕️ DFS와 ↔️ BFS

Haizel·2023년 12월 19일

💡 알바알천 프로젝트

목록 보기

10/11

📊 그래프 & 탐색

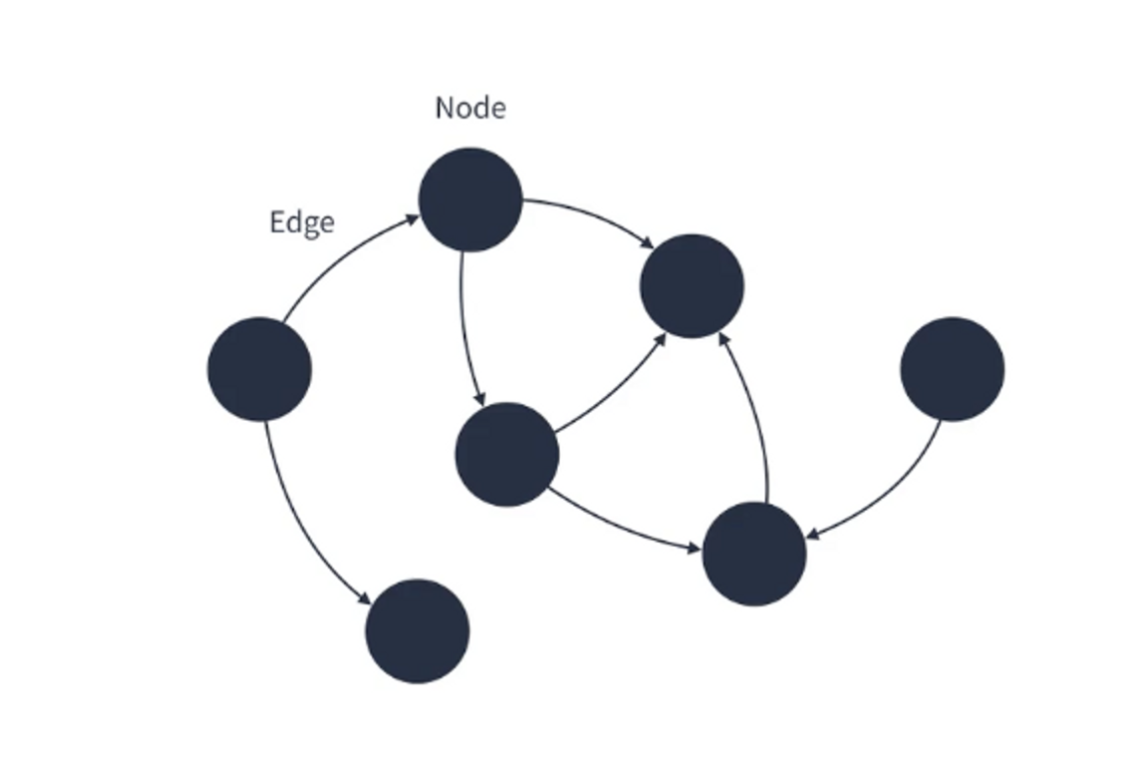
그래프(gragh) : 정점(node)과 그 정점을 연결하는 간선(edge)으로 이루어진 자료구조

그래프 탐색 : 원하는 데이터를 찾기 위해 하나의 정점에서 시작해 차례대로 모든 정점을 한 번씩 방문하는 것

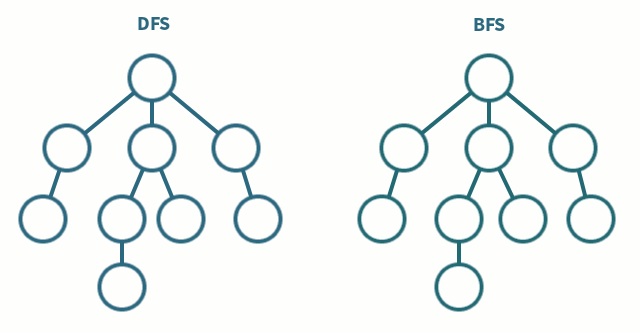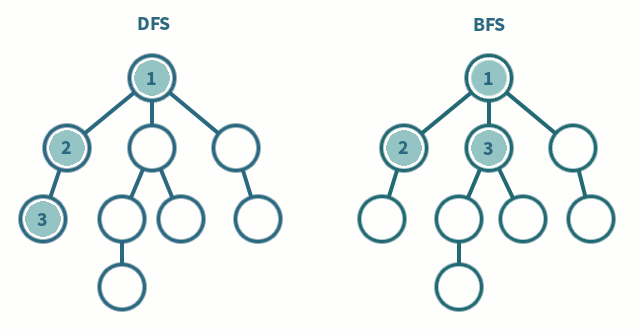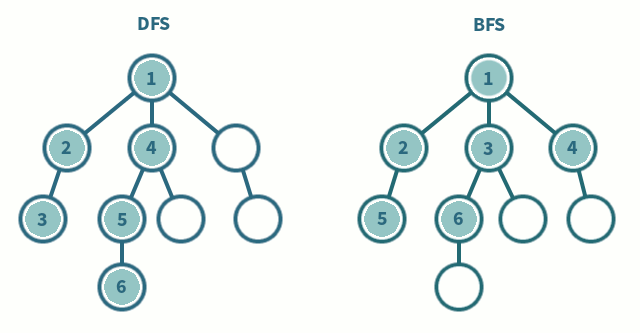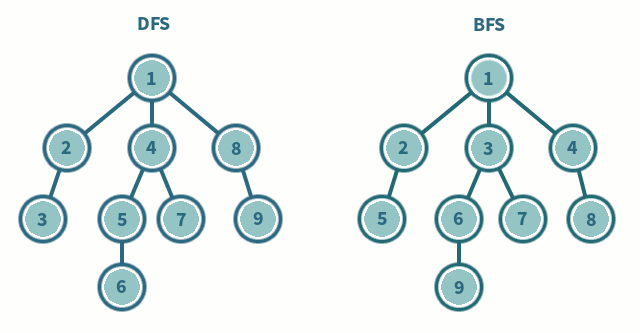
🦒 깊이 우선 탐색 (DFS, Depth - First Search)

그래프 탐색 알고리즘으로, 그래프와 트리의 깊은 부분을 우선적으로 탐색하는 알고리즘
Root Node(또는 다른 임의의 노드)에서 시작하여 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방식

⚒️ DFS 동작 방식

스택(Stack) 자료구조 또는 재귀함수를 이용한다.

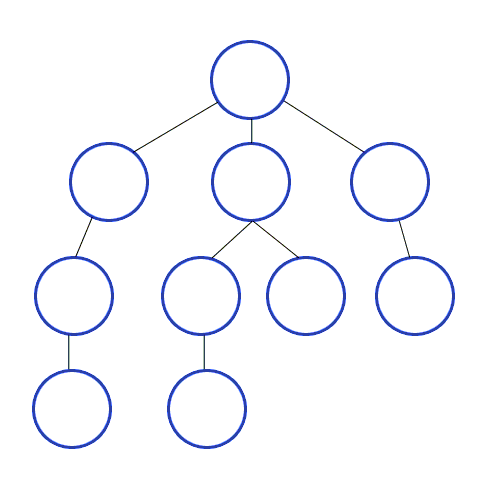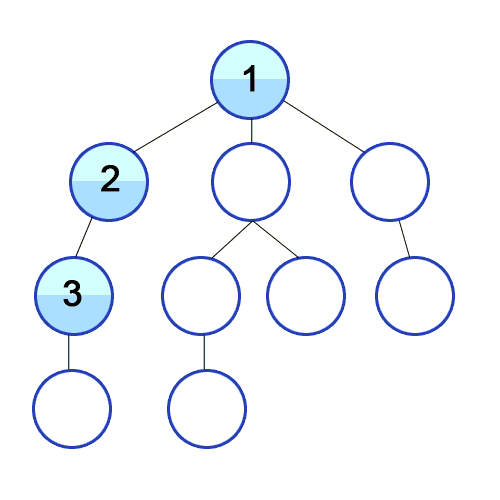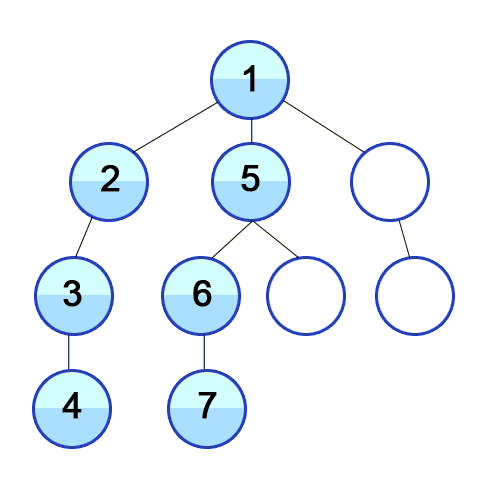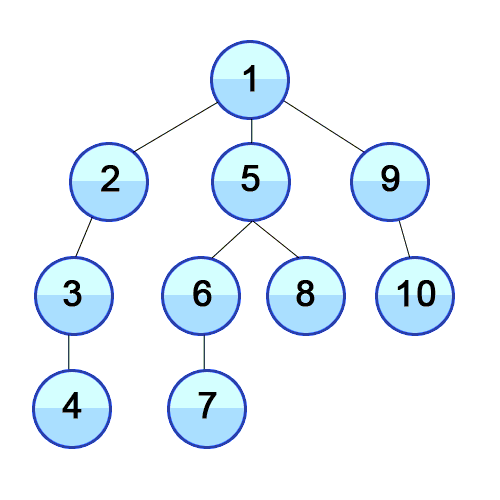
탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면, 해당 노드를 스택에 넣고 방문 처리를 한다.

2-1. 인접 노드가 여러 개라면 번호가 낮은 순부터 처리

2-2. 방문하지 않은 인접 노드가 없다면 스택에서 최상단 노드를 꺼낸다.
2번 과정을 더 이상 수행할 수 없을 때까지 반복한다.

👀 DFS 알고리즘 예제

프로그래머스 - 타겟 넘버

function solution(numbers, target) {
    let answer = 0;
    
    dfs(0, 0);
    
    function dfs(index, sum) {
        if(index === numbers.length) {
            if (sum === target) {
                answer++;
             }
            return;
        }
        
        dfs(index + 1, sum + numbers[index]);
        dfs(index + 1, sum - numbers[index]);
    }
    
    return answer;
}

console.log(solution([1, 1, 1, 1, 1], 3)); // 5
console.log(solution([4, 1, 2, 1], 4)); // ); // 2

// 작동 순서
// dfs(0, 0)
// -> dfs(1, 0)
//   -> dfs(1 + 1, 0 + 1)
//     -> dfs(2 + 1, 1 + 1)
//       -> dfs(3 + 1, 2 + 1)
//         -> dfs(4 + 1, 3 + 1)
//           -> dfs(5, 4 + 1)   // 함수 종료
//         -> dfs(4 + 1, 3 - 1) // 뺄셈 연산 실행
//           -> dfs(5, 2 + 1)   // 함수 종료
//       -> dfs(3 + 1, 2 - 1)   // 뺄셈 연산 실행
//         -> dfs(4 + 1, 1 + 1) // 덧셈 연산 실행
// ... 반복

※ 그래프 그림을 이용해 잘 설명해두심 !

🦛 너비 우선 탐색 (BFS, Breadth - First Search)

그래프 탐색 알고리즘으로, 가까운 노드부터 우선 탐색하는 알고리즘
Root Node(또는 다른 임의의 노드)에서 시작하여 인접한 노드를 먼저 탐색하는 방식

⚒️ BFS 동작 방식

큐(Queue) 자료구조를 이용한다.

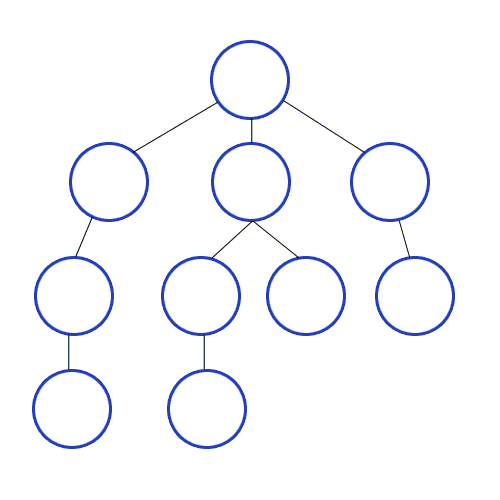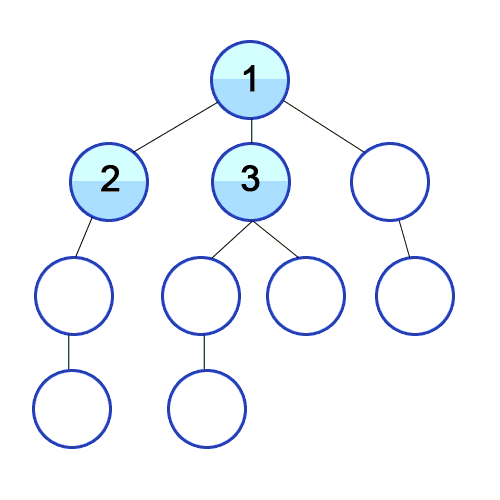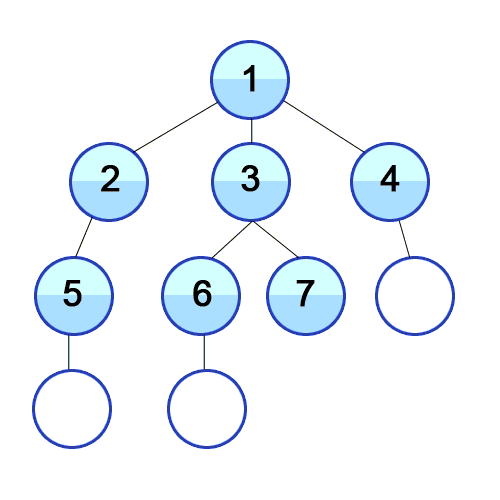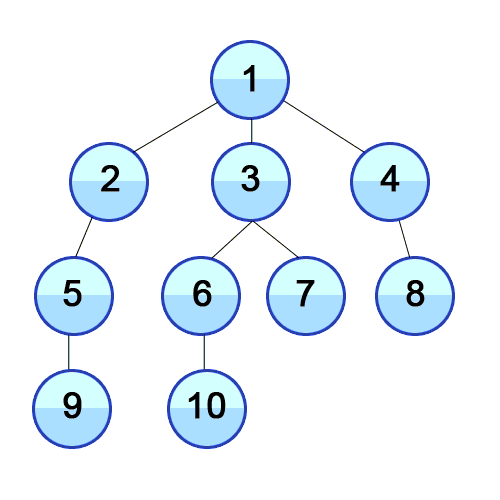
탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문처리를 한다.
2번 과정을 더 이상 수행할 수 없을 때까지 반복한다.

👀 BFS 알고리즘 예제

프로그래머스 - 게임 맵 최단거리

const solution = (maps) => {
  const [yLen, xLen] = [maps.length, maps[0].length]; // maps의 세로와 가로 길이
  const [goalY, goalX] = [yLen - 1, xLen - 1]; // 최종 목적지 좌표
  const dy = [0, 0, 1, -1]; // 좌우상하 움직일 때의 y좌표
  const dx = [-1, 1, 0, 0]; // 좌우상하 움직일 때의 x좌표
  const queue = [];

  queue.push([0, 0, 1]); // [y좌표, x좌표, 이동한 칸 수] 시작은 무조건 가장 좌측의 가장 상단에서 시작

  while (queue.length) {
    const [curY, curX, move] = queue.shift(); // 현재 좌표와 이동한 칸 수
    
    if (curY === goalY && curX === goalX) return move; //최종 좌표에 도착하면 이동한 수 리턴

    // 도착하지 않은 경우, 상하좌우 이동을 위한 4번의 반복문 동작
    for (let i = 0; i < 4; i++) {
      const moveY = curY + dy[i]; // 이동 후의 y좌표
      const moveX = curX + dx[i]; // 이동 후의 x좌표

      // 이동한 좌표가 map을 벗어나지 않고, 해당 좌표값이 1이라면
      if (moveY >= 0 && moveY < yLen && moveX >= 0 && moveX < xLen && maps[moveY][moveX] == 1) {
        queue.push([moveY, moveX, move + 1]); //이동한 좌표와 이동 횟수에 1을 더한 값을 큐에 담는다.
        maps[moveY][moveX] = 0; // 현재 좌표는 다시 지나지 않도록 0으로 변경한다.
      }
    }
  }
  return -1; // while문을 나왔다는 것은 도착할 수 없음을 의미함으로 -1을 반환
}

console.log(
  solution([
    [1, 0, 1, 1, 1],
    [1, 0, 1, 0, 1],
    [1, 0, 1, 1, 1],
    [1, 1, 1, 0, 1],
    [0, 0, 0, 0, 1],
  ])
); // 11
console.log(
  solution([
    [1, 0, 1, 1, 1],
    [1, 0, 1, 0, 1],
    [1, 0, 1, 1, 1],
    [1, 1, 1, 0, 0],
    [0, 0, 0, 0, 1],
  ])
); // -1

💡 DFS VS BFS

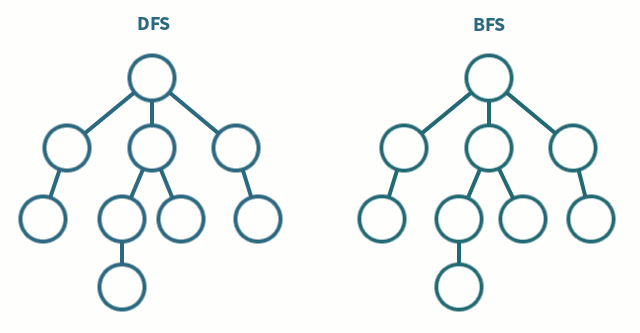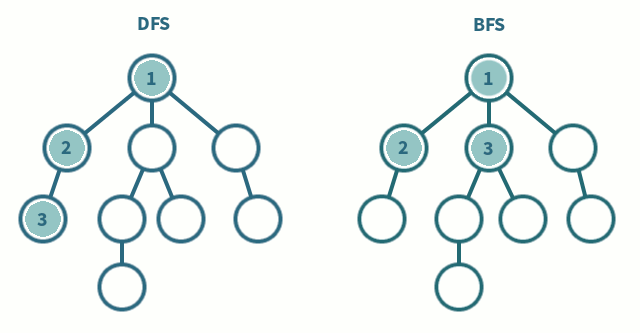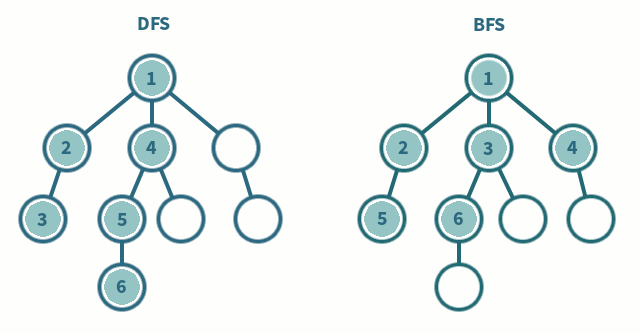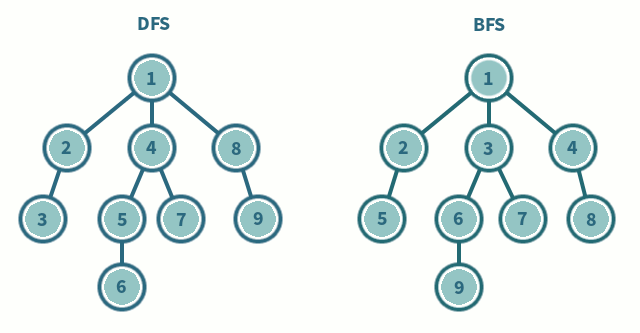
제목	깊이 우선 탐색(DFS)	너비 우선 탐색 (BFS)
탐색 과정	현재 정점에서 갈 수 있는 끝까지 방문하며 탐색	현재 정점에서 연결된 가까운 점들부터 탐색
구현 방법	스택 또는 재귀 함수 이용	큐 자료 구조 이용
적합	검색 대상 그래프가 매우 클 때	검색 시작 지점에서 원하는 대상이 별로 멀지 않을 때
대표 사례	경로의 특징을 저장해야 하는 경우	미로 찾기, 최단거리