이번주에 푼 문제

hakid29·2023년 9월 17일

1. [WHITEHAT2023] discrete_log

chall

from Crypto.Util.number import *
import os

def is_safe_prime(p):
    if not isPrime(p):
        return False
    
    if p.bit_length() > 1024:
        return False

    q = int(input("A large(> 999 bits) prime q such that q | p-1? (in hex) > "), 16)
    if q < 0 or q.bit_length() < 1000 or p % q != 1:
        return False
    
    return True

N = 1020
flag = b"fake flag" #로컬에서 해보느라 바꿨다.
x = flag + os.urandom(N // 8 - len(flag))
x = bytes_to_long(x)

for _ in range(77):
    p = int(input("prime modulus p? (in hex) > "), 16)
    if not is_safe_prime(p):
        print("invalid p..")
        exit(-1)

    g = bytes_to_long(os.urandom(N // 8))
    print(f"g = {hex(g)[2:]}")

    y = pow(g, x, p)
    print(f"g^x = {hex(y)[2:]}")

print("bye..")

$p$ 를 입력받고, $g$ 와 $g^x (mod \ p)$ 를 준다. (77번) 단, $q \ | \ p-1$ 인 1000비트 이상의 소수 $q$ 가 있어야 하며, $p$ 는 1024비트를 넘길 수 없다.

따라서, 남은 24비트를 77번 모아서 crt를 하면 충분하다. (flag는 1024비트 정도이므로 넉넉하게 구할 수 있다.) 처음엔 sage의 discrete_log함수를 썼는데, 12비트 정도의 소수에 대하여는 직접 브포하는게 더 빨라서 직접 구현했다.

exploit code

from Crypto.Util.number import *
from pwn import *
from sage.all import crt

def gen():
    p1 = getPrime(1000)
    while(1):
        p2, p3 = getPrime(12), getPrime(12)
        p = p1*p2*p3*2+1
        if p.bit_length() <= 1024 and isPrime(p) and p2 not in mod:
            break
    return p1, p2, p3, p

def dlp(g, gx, p):
    for i in range(p):
        if pow(g, i, p) == gx:
            return i

r = remote("43.201.97.135", int(3667))

mod = []
rr = []

for _ in range(77):
    p1, p2, p3, p = gen()
    r.sendline(f"{hex(p)}")
    r.recvuntil(b"hex) > ")
    r.sendline(f"{hex(p1)}")
    r.recvuntil(b"g = ")
    g = int(r.recvline().strip(), 16)
    r.recvuntil(b"g^x = ")
    gx = int(r.recvline().strip(), 16)

    dlp1 = dlp(pow(g, (p-1)//p2, p), pow(gx, (p-1)//p2, p), p)
    mod.append(p2)
    rr.append(int(dlp1))
    dlp2 = dlp(pow(g, (p-1)//p3, p), pow(gx, (p-1)//p3, p), p)
    mod.append(p3)
    rr.append(int(dlp2))

print(long_to_bytes(int(crt(rr, mod))))
#whitehat2023{789f4970bfceac553bffbc5633993fd169b2d3f2c3c830bde45e673d4f20c6de160751eb232872fe4925a68f75c2dd866d0d592a01}
r.interactive()

whitehat2023{789f4970bfceac553bffbc5633993fd169b2d3f2c3c830bde45e673d4f20c6de160751eb232872fe4925a68f75c2dd866d0d592a01}

2. [SECCON CTF 2023] RSA 4.0

chall (sage)

import os

from Crypto.Util.number import bytes_to_long, getStrongPrime

m = bytes_to_long(os.getenvb(b"FLAG", b"FAKEFLAG{THIS_IS_FAKE}"))
e = 0x10001
p = getStrongPrime(1024, e=e)
q = getStrongPrime(1024, e=e)
n = p * q
assert m < n
Q = QuaternionAlgebra(Zmod(n), -1, -1)
i, j, k = Q.gens()
enc = (
    1 * m
    + (3 * m + 1 * p + 337 * q) * i
    + (3 * m + 13 * p + 37 * q) * j
    + (7 * m + 133 * p + 7 * q) * k
) ** e
print(f"{n = }")
print(f"{e = }")
print(f"{enc = }")

사원수(Quaternion)가 나왔다. 사원수는 복소수를 확장한 체계로, 네 개의 실수 성분 ( $1, i, j, k$ )을 가지며, 덧셈, 곱셈의 결합법칙 및 덧셈의 교환법칙을 만족시키지만 곱셈의 교환법칙은 성립하지 않는다.
사원수의 집합 ${\mathbb H}$ 는 $\mathbb{R}^4 = \{a_0 + a_1i + a_2j + a_3k : a_0, a_1, a_2, a_3 ∈\mathbb{R} \}$ 이다. 기저 $\{ 1, i, j, k\}$ 는 다음과 같은 연산을 만족한다.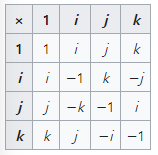

문제에서는 $\{m + (3m+p+337q)i + (3m+13p+37q)j + (7m+133p+7q)k\}^e$ 와 $n, e$ 가 주어졌다. 사원수의 집합에서 거듭제곱이 어떤 식으로 이루어지는지 찾아보았다.
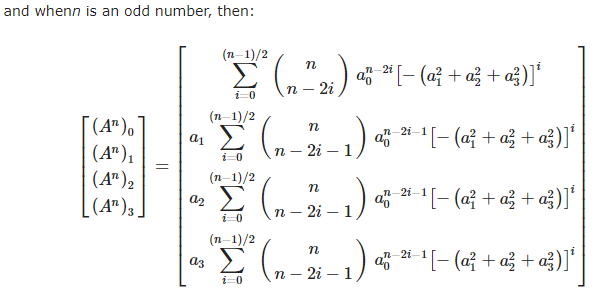reference : https://www.scirp.org/journal/paperinformation.aspx?paperid=116312

꽤나 복잡해 보이지만, 중요한 사실은 $n$ 제곱 했을 때, $i, j, k$ 의 계수의 비가 $a_1 : a_2 : a_3$ 라는 것이다. 이제 수식을 통해 살펴보자.

주어진 enc를 $b_0+b_1i+b_2j+b_3k$ 라고 하자.

b_1 : b_2 : b_3 = a_1 : a_2 : a_3

l_1 ≡ b_1b_2^{-1} ≡ a_1a_2^{-1} \ (mod \ n)

l_2 ≡ b_2b_3^{-1} ≡ a_2a_3^{-1} \ (mod \ n)

l_3 ≡ b_3b_1^{-1} ≡ a_3a_1^{-1} \ (mod \ n)

이므로

m_1 ≡ l_1a_2 - a_1 ≡ 0\ (mod \ n)

m_2 ≡ l_2a_3 - a_2 ≡ 0\ (mod \ n)

m_3 ≡ l_3a_1 - a_3 ≡ 0\ (mod \ n)

이다. 여기서 각각의 $a_i$ 는 $xm + yp + zq$ 꼴이므로 $m$ 을 소거한다면 $p$ 의 계수는 $q$ 의 배수가 될 수밖에 없고, $q$ 의 계수는 $p$ 의 계수가 될 수밖에 없다. 이를 코드로 보자.

leaking p, q (sage)

from Crypto.Util.number import *

n = 24872021325220256807454685550051664385270234794214413640899222873349265041897698942179745264628886444843936788046461273130347947293134447971213366009115689414264642605438643804813680767747014691971929645215382160557083245742340043385689944268138610186373780437485231877752933652320663858810427971106170059463601595006391073927194512124601928964813763052148657220845548046841237699017168286609835799813635564372682635612722890934578765797156432068449168053296617922489740666171866398517122799604532749283529271598232365042243492016089416298371516093933466381558297769513544950617454777689674801163035308121219081809467
e = 65537

Q.<i,j,k> = QuaternionAlgebra(Zmod(n), -1, -1)
enc = 3859728242860779998500245827824643011031182038976286035325209177561306523157077514772157957170475592309362631020979427907103610597898945426993614901767468098095010971836640454364234772978503167875298045774311291740824611786880849602974611016313651468361669338020331880259928969457255469579663017102640555015734482731890405522757985802082583300838209107911617815694578975817745782743203495107318667111104882994250616348383832987201616468973995462070255337923156614148218730987307161335625736122244817469974403678460213399052200814122255105544573927370423504309249212003649608881714115802854352284801298522985364992841 + 6689400988469336941290409439097720802889756496874465514203924923612416113717282667321908985103298019191113140239387801253466762593814350435047233088038044902433467651291903183405705080977679431528198024945921265445106468212962845547091599919008352051426009980329461007763212773358809391005850095961625042930422795445326743156495371981183105369799111219324695409896763869363969605501957524747716457126557615625815503861788352889135785579006785498195231741997934782780728866125488514068411960643904511224086647859058006472875473225695641287267610159704735294148907843394274092665622496223560673920367014991704447470344*i + 1425535224682533054692632153056888664907065024789232886308473909082337416786879221014972907213731240332278899126018247174859147121923692024420221262194523422785798197856518206508716047860471557004098274123870337912664160290690918788335238938208868363602574049572982498078216870780634694750710402353203621500287688744360281985793220035763469368517282385600578060642616443360598043313771383051760844966304306373372936321033698037647769588864584716070117876256372995523669859957654373351077969273910814003682705611267982200795979916283790161349821926490496096284763527696746485527643315156665082531990553153495043841613*j + 16939641902797542358954398454693773109828645853205801192220966778707379690160425812357360275630857752612391129705744211238057564114356027205464621658979245715243171261351328848491885377078864601014889472906967998503454246639030025900184373900964200415367983329654223213873342814827852864400395905048614694659842857369371845184915252563533413447471945691935551119149323541065035997716667873333295568018189682043599379592763126488255877418142891649422421776838694214872296853180292491137387225104189612300121323951103544193685306688963647668884425837634374966829437978854408218992213680164673972942664618735198830200420*k

b0, b1, b2, b3 = enc[0], enc[1], enc[2], enc[3]
c1 = [3, 1, 337]
c2 = [3, 13, 37]
c3 = [7, 133, 7]

l1 = b1*inverse(b2, n)%n
l2 = b2*inverse(b3, n)%n
l3 = b3*inverse(b1, n)%n

m1 = vector(c2)*l1 - vector(c1)
m2 = vector(c3)*l2 - vector(c2)
m3 = vector(c1)*l3 - vector(c3)
leak1 = m1*m2[0] - m2*m1[0]
leak2 = m1*m3[0] - m3*m1[0]

여기서 $leak1$ 을 출력해보면 $m$ 이 잘 소거된 것을 볼 수 있다. 따라서 leak[1]은 $q$ 의 배수, leak[2]는 $p$ 의 배수가 된다. 따라서

q \ | \ leak[1], \ p \ | \ leak[2]

를 만족한다.

p = GCD(leak1[2], n)
q = n//p
assert p*q == n

이제 $m1$ 에서 $p, q$ 를 대입만 하면 $m$ 을 leak할 수 있다.

print(long_to_bytes(int((m1[1]*p + m1[2]*q)*inverse(-m1[0], n) % n)).decode())

exploit code (sage)

from Crypto.Util.number import *

n = 24872021325220256807454685550051664385270234794214413640899222873349265041897698942179745264628886444843936788046461273130347947293134447971213366009115689414264642605438643804813680767747014691971929645215382160557083245742340043385689944268138610186373780437485231877752933652320663858810427971106170059463601595006391073927194512124601928964813763052148657220845548046841237699017168286609835799813635564372682635612722890934578765797156432068449168053296617922489740666171866398517122799604532749283529271598232365042243492016089416298371516093933466381558297769513544950617454777689674801163035308121219081809467
e = 65537

Q.<i,j,k> = QuaternionAlgebra(Zmod(n), -1, -1)
enc = 3859728242860779998500245827824643011031182038976286035325209177561306523157077514772157957170475592309362631020979427907103610597898945426993614901767468098095010971836640454364234772978503167875298045774311291740824611786880849602974611016313651468361669338020331880259928969457255469579663017102640555015734482731890405522757985802082583300838209107911617815694578975817745782743203495107318667111104882994250616348383832987201616468973995462070255337923156614148218730987307161335625736122244817469974403678460213399052200814122255105544573927370423504309249212003649608881714115802854352284801298522985364992841 + 6689400988469336941290409439097720802889756496874465514203924923612416113717282667321908985103298019191113140239387801253466762593814350435047233088038044902433467651291903183405705080977679431528198024945921265445106468212962845547091599919008352051426009980329461007763212773358809391005850095961625042930422795445326743156495371981183105369799111219324695409896763869363969605501957524747716457126557615625815503861788352889135785579006785498195231741997934782780728866125488514068411960643904511224086647859058006472875473225695641287267610159704735294148907843394274092665622496223560673920367014991704447470344*i + 1425535224682533054692632153056888664907065024789232886308473909082337416786879221014972907213731240332278899126018247174859147121923692024420221262194523422785798197856518206508716047860471557004098274123870337912664160290690918788335238938208868363602574049572982498078216870780634694750710402353203621500287688744360281985793220035763469368517282385600578060642616443360598043313771383051760844966304306373372936321033698037647769588864584716070117876256372995523669859957654373351077969273910814003682705611267982200795979916283790161349821926490496096284763527696746485527643315156665082531990553153495043841613*j + 16939641902797542358954398454693773109828645853205801192220966778707379690160425812357360275630857752612391129705744211238057564114356027205464621658979245715243171261351328848491885377078864601014889472906967998503454246639030025900184373900964200415367983329654223213873342814827852864400395905048614694659842857369371845184915252563533413447471945691935551119149323541065035997716667873333295568018189682043599379592763126488255877418142891649422421776838694214872296853180292491137387225104189612300121323951103544193685306688963647668884425837634374966829437978854408218992213680164673972942664618735198830200420*k

b0, b1, b2, b3 = enc[0], enc[1], enc[2], enc[3]
c1 = [3, 1, 337]
c2 = [3, 13, 37]
c3 = [7, 133, 7]

l1 = b1*inverse(b2, n)%n
l2 = b2*inverse(b3, n)%n
l3 = b3*inverse(b1, n)%n

m1 = vector(c2)*l1 - vector(c1)
m2 = vector(c3)*l2 - vector(c2)
m3 = vector(c1)*l3 - vector(c3)
leak1 = m1*m2[0] - m2*m1[0]
leak2 = m1*m3[0] - m3*m1[0] 
print(GCD(leak1[-1], n))

p = 141476557596579833574668265391714090690337192180322027886044593295709932858584782075511294793548739215434755212948359663229724283952681236596748859748966677701274874954135379817920423421375005329923490408880041127221023498920731140628880767831913618754023389828289551122285903550392137095478916519269190379889
q = n//p
assert p*q == n
print(long_to_bytes(int((m1[1]*p + m1[2]*q)*inverse(-m1[0], n) % n)).decode())

SECCON{pr0m153_m3!d0_n07_3ncryp7_p_0r_q_3v3n_w17h_r54_4.0}

처음 보는 개념이 나왔는데 풀어서 뿌듯했다.🤭🤭

hakid29

이전 포스트

Quotient Ring and isomorphism

다음 포스트