[백준BOJ] 16998번 - It’s a Mod, Mod, Mod, Mod World

문제

주어진 세 개의 정수 p, q, r에 대해서
$\displaystyle\sum_{i=1}^{n}{((p \cdot i) \text{ mod } q)}$
를 계산시오!

(*주의* 전체 합에는 모듈로 연산을 하지 않습니다!)

입력

W: 케이스의 수.
($1\le W \le 10^5$)

각 케이스별로 p, q, n이 차례로 입력된다.
($1\le p,\ q,\ n\le 10^6$)

---

풀이과정!

채택된 아이디어는 ⭐로 표시했습니다!!
주요한 흐름만 보고 싶다면 ⭐만 보면 됩니다!
.

생각 1. 수학박치기!

주의사항이 왜 붙었나 생각해보면,
정답이 전체 합에 나머지 연산을 하는 것이었다면
문제는 아래와 같이 단순화 될 수 있기 때문입니다.

$\displaystyle (\sum_{i=1}^{n}p \cdot i)\text{ mod q} = (p \cdot {n\cdot(n-1)\over{2}})\text{ mod q}$

슬프지만 다른 방법을 모색해야 할 거 같습니다...(유유,😢)
.
.

생각 2. 반복문박치기!

보이는 대로의 구현을 해보겠습니다!!

result = 0;

for(int i=1; i<=n; i++)
	result += p*i%q;

무지막지한 n 값에 의하여 시간 초과가 발생할 것으로 보입니다... (유유,,😢)

이제부터는 더이상 무얼 할 구석이 없으므로
여기서 뭘 더 어떻게 최적화를 할 수 있을까 고민해봤습니다,,,
.
.

생각 3. 무언가 더 수학스러운 것,

반복되는 모듈러들의 합을 단숨에 계산할 수 있는 어떤 수학적 성질이 있을까?

(예를 들면 막 나머지값이 반복된다거나 하는,,,)

슬프게도 p, q, n 사이에 어떤 관계도 제시되지 않아 어려워보입니다... (유유,,,😢)

(만약 p와 q가 서로소였다면 기약잉여계 성질을 사용할 여지가 있습니다. 궁금하다면 페르마 소정리의 증명을 찾아보세요!!)

.

생각 4. floor와 약간의 트릭!🪄⭐

$pi \text{ mod q }$자체를 단순화할 순 없을까?

적절한 정수 n에 대해서 $pi = qn + r$로 표현할 수 있습니다.

해당 정수 n은 $\lfloor {pi\over q}\rfloor$로 표현이 가능하다. (조건이 중요합니다 꼭 기억하십쇼!!)
$\displaystyle pi = q\lfloor {pi\over q}\rfloor + r$
$\displaystyle r = pi- q\lfloor {pi\over q}\rfloor = (pi \text{ mod q})$

이를 이용해 본래 식을 표현하면

$\displaystyle\sum_{i=1}^{n}{((p \cdot i) \text{ mod } q)}\ =\ \sum_{i=1}^{n}{(pi- q\lfloor {pi\over q}\rfloor)} \ =\ p\cdot {n(n+1)\over2} - q\sum_{i=1}^{n}\lfloor {pi\over q}\rfloor$

까지 정리가 가능합니다!

여기서부터는 목표가 조금 더 구체적으로 변해,
$\displaystyle\sum_{i=1}^{n}\lfloor {pi\over q}\rfloor$를 어떻게 잘 구할 수만 있다면 문제의 정답에 근접하게 될 것입니다!!!

.

생각 5. floor와 더 많은 트릭!🪄⭐

$\displaystyle\sum_{i=1}^{n}\lfloor {pi\over q}\rfloor$를 어떻게 다룰 수 있을까. - 첫번째 시도

$pi\over q$는 다음과 같이 변형될 여지가 있습니다.

$\displaystyle{p\over q} = \lfloor{p\over q}\rfloor + r\ (0 \le r < 1)$

코드에 쓰기 좋은 형태로 변신시켜보자면,

$\displaystyle{p\over q} = \lfloor{p\over q}\rfloor + {p\mod q \over q}$

p/q + p%q/q 

여기서 floor 연산의 성질 하나를 더 생각해보자면,
어떤 정수 n과 실수 a에 대해서 다음이 성립합니다!!!!

$\lfloor n + a\rfloor = n + \lfloor a\rfloor$

적용하자면,

$\displaystyle\lfloor {pi\over q}\rfloor = \lfloor \lfloor {p\over q}\rfloor{} i \ +\ {p \mod q \over q}i\rfloor = \lfloor {p\over q}\rfloor i + \lfloor {p \mod q\over q} i\rfloor$

($p\over q$를 $\lfloor{p\over q}\rfloor + {p \mod q \over q}$ 로 변신시켰습니다)

이 아이디어 매우 ⭐중요⭐합니다!
이를 적용하면 여기까지도 정리 가능합니다.

$\displaystyle\sum_{i=1}^{n}\lfloor {pi\over q}\rfloor = \sum_{i=1}^{n}(\lfloor {p\over q}\rfloor i + \lfloor {p \mod q\over q} i\rfloor) = \lfloor{p\over q}\rfloor\cdot {n(n+1)\over 2} + \sum_{i=1}^{n}\lfloor {p \mod q\over q}i\rfloor$

이 부분을 코드로 적어보겠습니다. (코드로 작성하고 무언가 힌트를 얻었기 때문입니다)!

result = p/q * n * (n+1) / 2;

for(int i=1; i<=n; i++)
	result += p%q*i/q;

제일 처음 반복문박치기 코드를 가져와 비교해보자면,

result = 0;

for(int i=1; i<=n; i++)
	result += p*i%q;

반복문 부분을 보자면,
p에 p%q를 대입한 것과 맥이 상통합니다!
f(p, q, n) = (생략...) + f(p%q, q, n) ⭐

생각 6. 그래프를 그리면 보이는 것⭐

$\displaystyle\sum_{i=1}^{n}\lfloor {pi\over q}\rfloor$를 어떻게 다룰 수 있을까. - 두번째 시도

그러나 여전히 $\displaystyle\sum_{i=1}^{n}\lfloor {pi\over q}\rfloor$는 계산이 오래 걸리므로 시그마의 범위를 어떻게든 하지 않으면 안됩니다.

$f(x) = {p\over q}x$ 그래프를 그려보겠습니다.

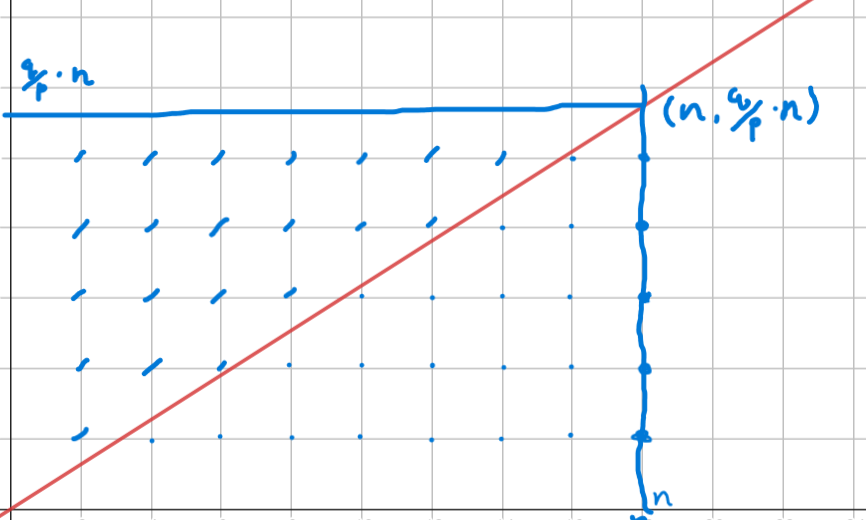
이때,
$\lfloor {pi\over q}\rfloor$는, $f(i) = {p\over q}i$ 아래의 양수 격자점들의 갯수로,

$\displaystyle\sum_{i=1}^{n}\lfloor {pi\over q}\rfloor$는 그래프를 포함한 그 아래의 모든 양수 격자점들의 갯수를 의미합니다.

이를 조금 비틀어서 생각해보면, 해당 식을 이렇게 바꿔볼만도 합니다.
$\displaystyle\sum_{i=1}^{n}\lfloor {pi\over q}\rfloor$ = (사각형 내 모든 격자점 - 포함되지 않는 격자점의 수)
이는 바꿔말하면, 해당 그래프를

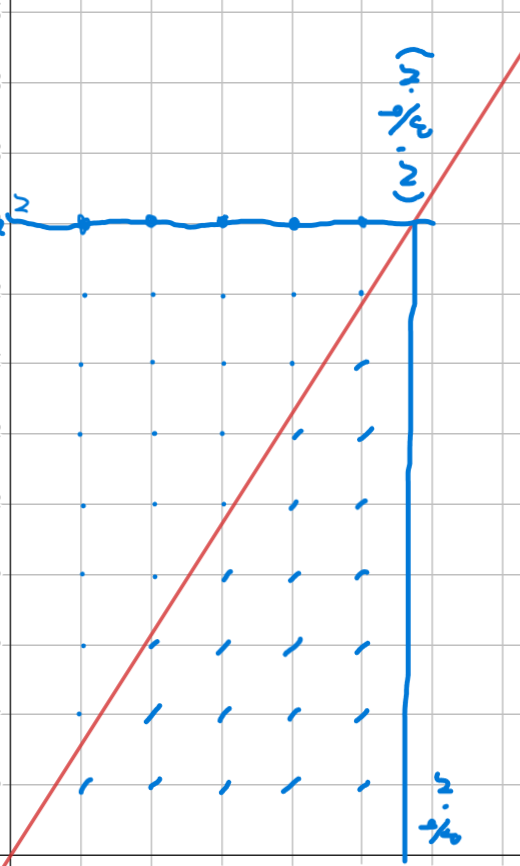
이렇게 뒤집고 사각형 내부의 격자 중, 그래프 아래의 격자를 빼는 것으로 생각할 수 있습니다.
이때의 그래프 포함 그래프 아래의 격자의 수는
$\displaystyle\sum_{i=1}^{\lfloor {p \over q}n\rfloor}\lfloor {qi\over p}\rfloor$ 입니다.
그 중 정확히 그래프 위에 있는 격자점들은 제외해야합니다.
그러한 점의 개수는 n까지의 숫자 중 q의 배수인 것의 개수이므로, $\displaystyle\lfloor {n \over q}\rfloor$입니다.
따라서 다음과 같은 식을 얻을 수 있습니다.

$\displaystyle\sum_{i=1}^{n}\lfloor {pi\over q}\rfloor = \lfloor{pn \over q}\rfloor n -(\sum_{i=1}^{\lfloor {p \over q}n\rfloor}\lfloor {qi\over p}\rfloor - \lfloor {n \over q}\rfloor)$

이는 p<q 인 상황에선 반복 횟수를 줄일 수 있습니다.
f(p, q, n) = (생략...) - f(q, p, p*n/q) ⭐

---

한 번 정리하고 코드를 볼까요?

$\displaystyle\sum_{i=1}^{n}\lfloor {pi\over q}\rfloor$ 연산을 가진 함수를 $sum(p,\ q,\ n)$라고 정의해봅시다.
그러면 다음이 성립합니다!
$\displaystyle sum(p, q, n) = \lfloor{p\over q}\rfloor\cdot {n(n+1)\over 2}\ +\ sum(p\mod q,\ q,\ n)$ ⭐ (p > q)
$\displaystyle sum(p, q, n) = \lfloor{pn \over q}\rfloor n + \lfloor {n \over q}\rfloor \ -\ sum(q,\ p,\ \lfloor{pn\over q}\rfloor)$ ⭐ (p<q)

(첫번쩨에 조건이 붙은 것은, p>q가 아닐 때에는 무의미한 재귀가 되기 때문입니다.)

오... 이 흐름은 함수가 계속 함수를 아주 재귀적으로 구현할 수 있겠습니다.

sum(p, q, n){
    ...
    
    if(p > q)                                        
        return sum(p%q, q, n) + (p/q)*(n*(n+1)/2);
	else if(p < q)
    	return n * (p*n/q) + n/q - sum(q, p, p*n/q); 
}

재귀를 하려면 더 엄밀할 필요가 있어 보입니다.

sum(p, q, n) 에서
1. p=q인 경우를 생각해봅시다.
p==q일 때는 고민할 것도 없이 0입니다. p mod q는 0이기 때문입니다.

2. p = 0이면 결과값은 0입니다.

3. q = 1이면 결과값은 $\displaystyle p{n(n+1)\over2}$입니다.

4. n=0이어도 결과값은 0입니다.

작은 아이디어를 하나 추가해봅니다. p와 q는 함수 내에서 서로를 나누는 데에만 사용이 됩니다.
따라서 각각의 수에 최대공약수를 제해버려도 결과는 같습니다.
함수를 사용할 때 p와 q를 공배수를 제하고 사용한다 가정한다면
조건을 조금 더 깔끔하게 쓸 수 있겠습니다.

즉 다음과 같이 코드가 완성됩니다.

sum(p, q, n){
    if(p == 0 || n == 0)
    	return 0;
    if(q == 1)
        return p*n*(n+1)/2
    
    if(p >= q)                                        
        return sum(p%q, q, n) + (p/q)*(n*(n+1)/2);
	
    return n * (p*n/q) + n/q - sum(q, p, p*n/q); 
}

문제에서 요구하는 정답이
$\displaystyle\sum_{i=1}^{n}{((p \cdot i) \text{ mod } q)}\ =\ p\cdot {n(n+1)\over2} - q\sum_{i=1}^{n}\lfloor {pi\over q}\rfloor$
였던 것을 생각해보면
정답은p*n*(n+1)/2 - q*sum(p,q,n)로 계산됩니다.

정답 코드

#include<iostream>
#include<algorithm>

using namespace std;

typedef unsigned long long ull;

ull gcd(ull a, ull b){
    if(a < b) swap(a, b);

    if(b == 0)
        return a;

    return gcd(b, a%b);
}

ull sum(ull p, ull q, ull n){
    if(p == 0 || n == 0)
        return 0;
    if(q == 1)
        return p*n*(n+1)/2;

    if(p >= q)
        return sum(p%q, q, n) + (p/q)*(n*(n+1)/2);

    return n * (p*n/q) + n/q - sum(q, p, p*n/q);
}

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    int w;
    cin>>w;

    while(w--){
        ull p, q, n;
        cin>>p>>q>>n;

        ull g = gcd(p, q);
        ull s = sum(p/g, q/g, n);

        ull result = p*n*(n+1)/2 - q*s;
        cout<<result<<'\n';
    }
    return 0;
}

---