1. 시간복잡도란?

특정 문제를 푸는데 컴퓨터가 실행하는 연산 횟수이다. 예를들어 특정 두 수의 크기를 한번 비교하면 한번의 연산이 이루어지는 것이다. 시간복잡도는 아래와 같이 3가지로 이루어진다. 해당 시간복잡도는 프로그램의 입력값의 길이에 의해 결정된다. 하지만 표기법에서는 입력값의 길이를 n으로 지정한다. 그리고 항상 최악의 경우를 고려한다.

2. log N

해당 시간복잡도의 대표적인 연산은 이진탐색이다.

위에서 66을 찾기위해 중앙값과 비교하는 연산이 총 3번 일어나고

3. N*logN

해당 시간복잡도의 대표적인 연산은 병합정렬이다.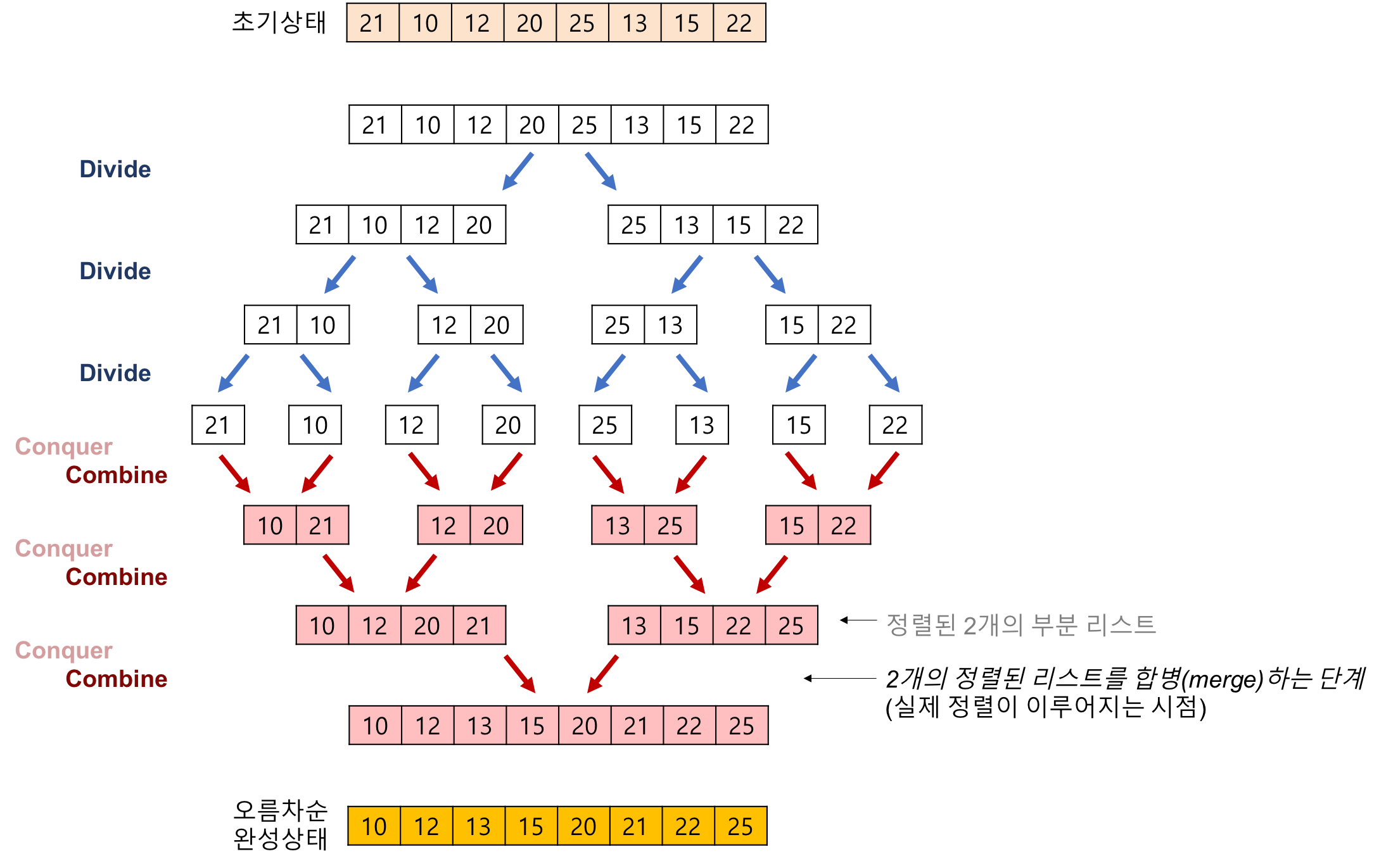
위에서 정렬하기 위해 각 층, 총 3개의 층에서 정렬이 한번씩 난다. 각 층마다 노드안에 포함되어 있는 숫자의 개수는 다르지만 층에서 봤을 때, 총8번의 정렬이 일어난다. 그리고 깊이는 3으로 8x3해서 총 24번이 일어난다. 시간복잡도로 따지면 n=8이므로 한층당 n번의 정렬이 일어나고 깊이는 logn이 된다. 따라서 병합정렬의 시간복잡도는 NlogN인 것이다.