🔍 Problem
이 문제는 N개의 퀸을 NxN 체스판에 놓을 수 있는 경우의 수를 구하는 문제이고 Input은 1과 15사이의 정수이며 Output 또한 경우의수, 즉 정수이다. 이것은 내가 놓은 체스가 마지막 행까지 왔을 때 경우의 수를 하나 추가하는 방법으로 문제를 풀 수 있다. 왜냐하면 N개의 퀸을 다 놓기 위해서는 체스판의 N번째 행, 즉 마지막 행까지 도달해야하기 때문이다. 따라서 이 문제는 트리 형태로 구성할 수 있고 N번째 행까지 체스를 놓은 경우에만 경우의 수를 하나 추가하면된다. 이것은 가지치기 문제로 분류할 수 있으며 결국 재귀를 사용하는 백트래킹 문제로 분류됨을 의미한다.
📒 해결과정
가. 퀸을 빠짐없이 N개만큼, 즉 N번째 행까지 체스판에 놓아야 하고 위에서 부터 아래로 놓는 방법을 사용할 것이다.**
나. 퀸을 놓은 개수가 사용자의 입력값과 같다면, 즉 마지막 행까지 퀸이 도달한면 해당 경우는 유망하다고 판단하고 경우의 수를 하나 올린다.
다. 나에 대한 대용을 트리로 구현해보자.
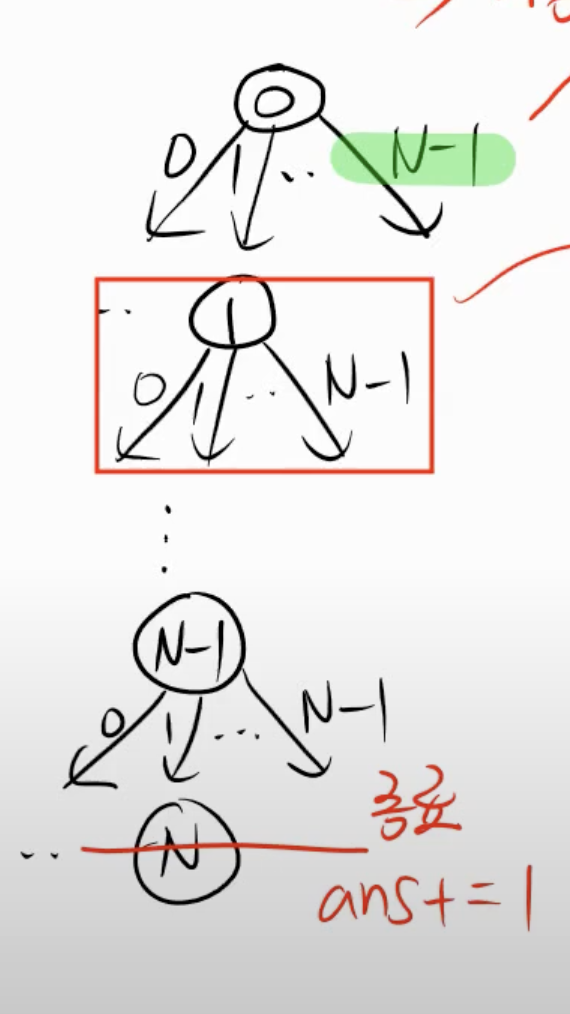
[트리 설명]
1] 루트 노드는 퀸을 0번째 놓았을 때의 노드이고 각 엣지(가지)는 열의 번호이다.
[0,1]에 퀸 위치 : root node : 0, 엣지 : 1
2] 해당 엣지를 통해서 다음 노드를 접근을 할 수 있지만 퀸을 놓을 수 있는가를 체크해야한다.라. 다의 2번에 해당하는 체크에 대한 함수를 작성한다.

0] 배열선언
가. 횡 체크 배열 v1 # v1[행] = 1
나. 왼쪽 대각선 체크 배열 v2 # v2[행+열] = 1 -> 놓여짐
다. 오른쪽 대각선 체크 배열 v3 # v3[행-열] = 1 -> 놓여짐
1] 해당 열에 놓을 수 있는지 체
if v1[열] == 1:
return true
2] 해당 대각 선에 놓을 수 있는지 체크
if v2[행+열] == 0:
return true
3] 2번과 비슷마.다의 종료 조건에 대해 작성
# 종료 건은 놓는 행의 위치(N번째 놓는 퀸)가 Input이랑 같을 때, N : input
if (N == row):
cnt+=1바. 다의 엣지를 통한 다음 노드로 이동하는 것은 for문과 dfs를 사용할 것이다.
for row in range(N-1): # 0~N-1 엣지
1. 놓을 수 있는 지 체크
1.1 놓을 수 있다면 놓기
1.2 dfs(row+1)
1.3 말 빼기사. 전체 의사 코드 작성
func dfs(row):
1. 종료 조건
#주의 result +=1 할 때, result 는 gloabal로 선언!
2. for문으로 노드 엣지(다음 열)로 이동(발 걸치기, 아직 엣지를 통해서 출발 한거 아님)
2.1 놓을 수 있는지 체크
2.1.1 놓을 수 있다면 놓고
2.1.2 dfs(row+1) #현재 엣지의 재귀를 함으로써 다음 노드로 이동 (요때 이동)
2.1.3 놓은거 회수
1. 열 방문 췍 배열
2. 왼쪽 대각선 방문 췍 배열
3. 오른쪽 대각선 방문 책 배열
💻 Code
#사용언어 : python
import sys
def dfs(row):
global result
if(row==N):
result+=1
return
for col in range(0,N):
if (v1[col]==0 and v2[col+row]==0 and v3[row-col]==0):
v1[col]=v2[col+row]=v3[row-col]=1
dfs(row+1)
v1[col]=v2[col+row]=v3[row-col]=0
N=int(sys.stdin.readline())
v1=[0]* N
v2=[0]*(2*N)
v3=[0]*len(v2)
result=0
dfs(0)
print(result)
🤔 느낀점
이것은 DFS를 사용한 백트래킹 문제로 처음엔 이 말이 무슨말인지 잘 모르겠는데 아직도 잘 모르겠다. 왜 BFS를 쓰는 걸까 ? 트리 형태로 생각해 내는것이 어렵고 문제를 많이 풀어봐야겠다. 그리고 처음에 dfs의 파라미터로 어떤것을 잡아야할지가 코드를 쉽게 만드느냐 어렵게 만드느냐를 결정할 것 같다.
그리고 두문제 더풀면 백준 골드다!!

