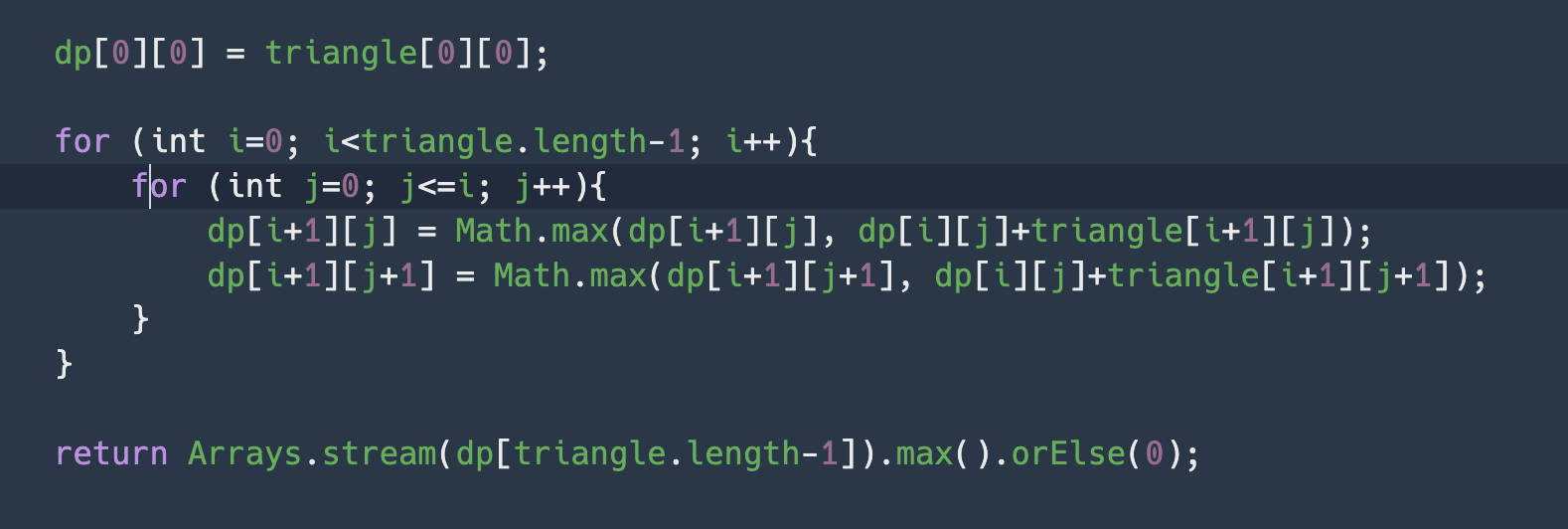
🔍 Problem
📃 Input&Output

🌁 문제 배경
가. 문제 설명
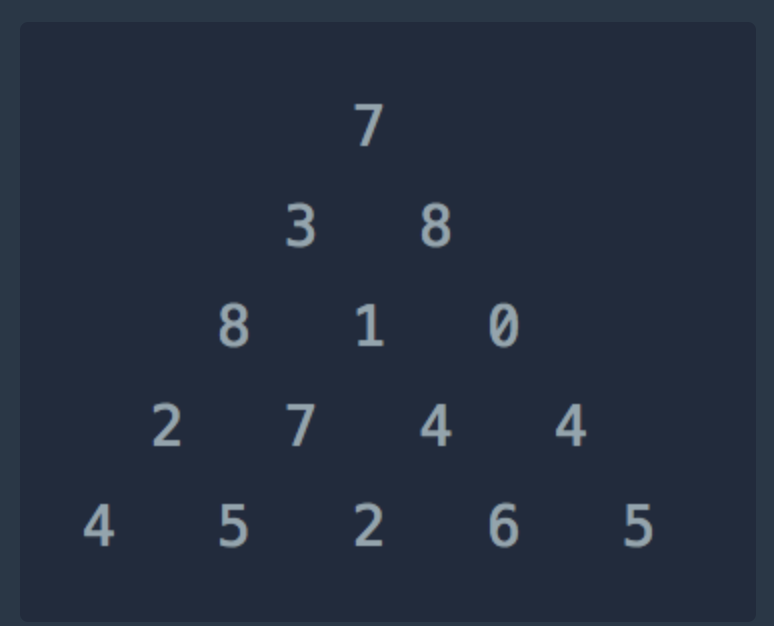
위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.
삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.
- 제한사항
1) 삼각형의 높이는 1 이상 500 이하입니다.
2) 삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.
나. 접근 방법
DP로 현재위치에서 다음 위치를 반영하는데, 해당 위치의 기존 값과 비교해서 더 큰값을 반영시킨다.
다. 문제 유형
DP( DP의 아주 기본적인 문제)
📒 수도 코드
가. triangle에 맞게 dp 배열을 만들고 0으로 초기화 후, dp[0][0] = triangle[0][0]]f
int answer = 0;
int[][] dp = new int[triangle.length][];
for (int i=0; i<dp.length; i++){
dp[i] = new int[dp.length];
}
dp[0][0] = triangle[0][0];나. 삼각형을 직각삼각형으로 만들어서 점화식 구현
위의 점화식이 의미하는 바는 현재 위치에서 아래 방향 위치 값, 오른쪽 대각선 방향 위치 값을 갱신시키는 것이고 그 방법은 이전 각각의 dp값과 현재 dp값+더해질 값들을 비교해서 둘 중에 큰 값을 각각의 dp값에 넣는 것이다.
다음 입력될 dp값을 현재 값에서 계산하는 형식이고, 갱신될 때마다 기존값과 비교해서 둘 중, 최대값으로 갱신하는 로직인 것이다.
다. 마지막 행에서 최대값 구하기
거쳐간 숫자의 최댓값을 return 하도록 최대값을 구하는 것이므로, 마지막 행은 모든 행을 반영한 행이므로 이 행에서 최대값을 구해주면 되는 것이다.
💻 Code
import java.util.*;
class Solution {
public int solution(int[][] triangle) {
int answer = 0;
int[][] dp = new int[triangle.length][];
for (int i=0; i<dp.length; i++){
dp[i] = new int[dp.length];
}
dp[0][0] = triangle[0][0];
for (int i=0; i<triangle.length-1; i++){
for (int j=0; j<=i; j++){
dp[i+1][j] = Math.max(dp[i+1][j], dp[i][j]+triangle[i+1][j]);
dp[i+1][j+1] = Math.max(dp[i+1][j+1], dp[i][j]+triangle[i+1][j+1]);
}
}
return Arrays.stream(dp[triangle.length-1]).max().orElse(0);
}
}🎸 기타
가. Arrays.stream(arr).max().orElse()
자바에서 배열을 Stream으로 변환하여, 해당 배열안 원소들의 최대값을 구하는 syntax이다.
🤔 느낀점
점화식 시점의 다양성을 느꼈다.
DP를 해결할 때, 점화식의 시점을 여러곳에 둘 수 있다는 것이 이 문제를 다시 풀어보면서 느꼈다. 필자가 알던 DP는 현재값이 갱신되기 전 이전 단계가 현재값에 어떻게 영향을 미칠까를 생각하면서 DP 점화식을 구현하고자 하였는데, 해당문제는 현재값이 다음값에 어떤 영향을 미칠까를 생각하면서 풀었던 문제이다.