암호 해시 기술과 공개키 암호 기술은 전자서명 같은 디지털 보안의 근간이 된다.
SHA-256은 SHA(Secure Hash Algorithm) 알고리즘의 한 종류로서 256비트로 구성되며 64자리 문자열을 반환한다. SHA-256은 미국의 국립표준기술연구소(NIST; National Institute of Standards and Technology)에 의해 공표된 표준 해시 알고리즘인 SHA-2 계열 중 하나이며 블록체인에서 가장 많이 채택하여 사용하고 있다. 이름에 내포되어 있듯
2^256만큼 경우의 수를 만들수 있다. 개인용 컴퓨터로 무차별 대입을 수행해 해시 충돌 사례를 찾으려고 할 때 많은 시간이 소요될 정도로 큰 숫자이므로 충돌로부터 비교적 안전하다고 평가된다.
http://wiki.hash.kr/index.php/SHA256
블록체인을 공부하다 보면 해싱 알고리즘은 블록체인 전반에 걸쳐서 사용되며 보안에 핵심적인 역할을 함을 알 수 있었다.
SHA-256 해시 함수는 어떤 길이의 값을 입력하더라도 256비트의 고정된 결과값을 출력한다.
이러한 비가역적인 특성은 합의 알고리즘을 비롯하여 전체적인 블록체인 알고리즘에 사용되는데,
이런 해싱 알고리즘의 원리가 궁금해서 찾아보게 되었다.
https://blog.naver.com/doksg/221854572659 - 공부한 블로그
https://seed.kisa.or.kr/kisa/Board/21/detailView.do - SHA-256 알고리즘
https://www.cs.rit.edu/~ark/lectures/onewayhash/onewayhash.shtml - 그림
해시 함수의 특징
1. 단방향성
2. 충돌 회피
3. 효율적 연산
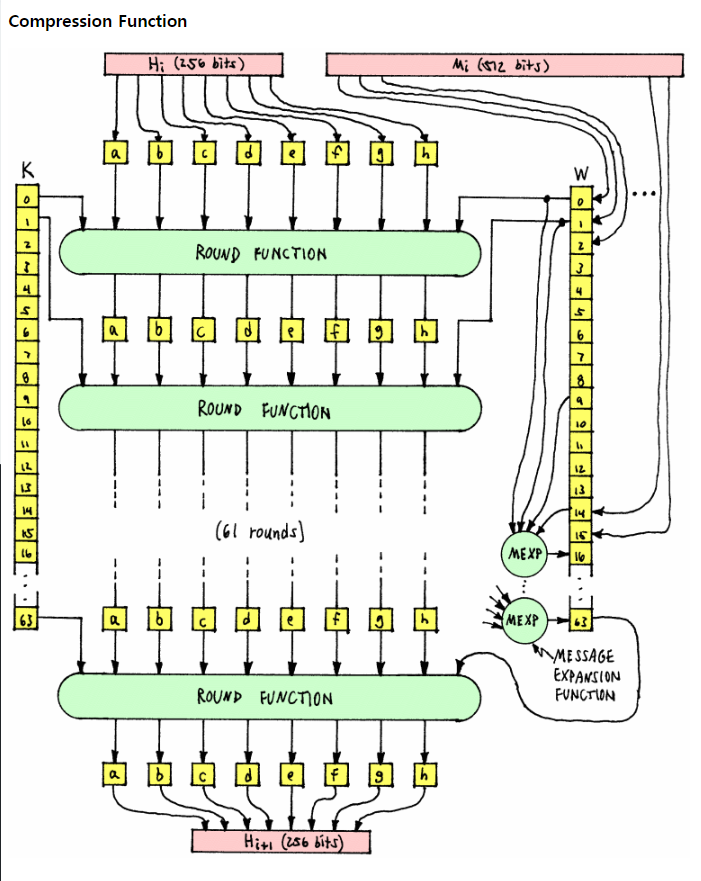
해시 알고리즘을 잘 설명한 그림이다.
MESSAGE 로 특정한 문자열이 들어오면 전처리 과정을 통해 W[64]로 변환하고,
W[64], K[64], H[8] 세 배열을 이용한 변환을 통해 해시 결과를 반환한다.
#define ROTR_ULONG(x, n) _lrotr((x), (n))
#define RR(x, n) ROTR_ULONG(x, n)
#define SS(x, n) (x >> n)
#define RHO0(x) (RR(x, 7) ^ RR(x, 18) ^ SS(x, 3))
#define RHO1(x) (RR(x, 17) ^ RR(x, 19) ^ SS(x, 10))
for (j = 0; j < 16; j++)
X[j] = GetData(Message[j]);
for (j = 16; j < 64; j++)
X[j] = RHO1(X[j - 2]) + X[j - 7] + RHO0(X[j - 15]) + X[j - 16];input 값 message를 W[64]로 전처리 하는 과정.
X[0]~X[15] 까지는 값을 그대로 가져오고,
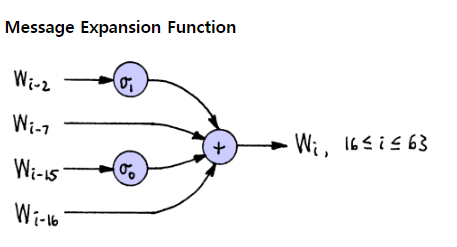
X[16]~X[64]는 각각의 index에서 다음 코드를 반복한다.
X[0]~X[15] 까지는 message를 그대로 가져오고, 그 뒤로는 셔플된 더미 데이터를 집어넣는 느낌인 것 같다.(maybe)
typedef struct{
UINT uChainVar[SHA256_DIGEST_VALUELEN / 4];
UINT uHighLength;
UINT uLowLength;
UINT remain_num;
BYTE szBuffer[SHA256_DIGEST_BLOCKLEN];
} SHA256_INFO;
void SHA256_Init( OUT SHA256_INFO *Info )
{
Info->uChainVar[0] = 0x6a09e667;
Info->uChainVar[1] = 0xbb67ae85;
Info->uChainVar[2] = 0x3c6ef372;
Info->uChainVar[3] = 0xa54ff53a;
Info->uChainVar[4] = 0x510e527f;
Info->uChainVar[5] = 0x9b05688c;
Info->uChainVar[6] = 0x1f83d9ab;
Info->uChainVar[7] = 0x5be0cd19;
Info->uHighLength = Info->uLowLength = Info->remain_num = 0;
}Info->uChainVar == H[8]으로, 32bit씩 8개 총 256bit로 구성되어 있는데,
8개의 가장 작은 소수 [2,3,5,7,11,13,17,19]의 제곱 근의 소수점 이하 32bit의 값.
const UINT SHA256_K[64] =
{
0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1,
0x923f82a4, 0xab1c5ed5, 0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3,
0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174, 0xe49b69c1, 0xefbe4786,
0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147,
0x06ca6351, 0x14292967, 0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13,
0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85, 0xa2bfe8a1, 0xa81a664b,
0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a,
0x5b9cca4f, 0x682e6ff3, 0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208,
0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2
};64개의 가장 작은 소수
2, 3, 5, 7, 11, 13, 17, 19, 23, 29,
31, 37, 41, 43, 47, 53, 59, 61, 67, 71,
73, 79, 83, 89, 97, 101, 103, 107, 109, 113,
127, 131, 137, 139, 149, 151, 157, 163, 167, 173,
179, 181, 191, 193, 197, 199, 211, 223, 227, 229,
233, 239, 241, 251, 257, 263, 269, 271, 277, 281,
283, 293, 307, 311
의 세 제곱의 소수점 이하 32bit의 값
이제 최종적으로 Rounded Function만 수행하면 된다.
#define Ch(x, y, z) ((x & y) ^ ((~x) & z))
#define Maj(x, y, z) ((x & y) ^ (x & z) ^ (y & z))
#define Sigma0(x) (RR(x, 2) ^ RR(x, 13) ^ RR(x, 22))
#define Sigma1(x) (RR(x, 6) ^ RR(x, 11) ^ RR(x, 25))
#define FF(a, b, c, d, e, f, g, h, j) { \
T1 = h + Sigma1(e) + Ch(e, f, g) + SHA256_K[j] + X[j]; \
d += T1; \
h = T1 + Sigma0(a) + Maj(a, b, c); \
}
a = ChainVar[0];
b = ChainVar[1];
c = ChainVar[2];
d = ChainVar[3];
e = ChainVar[4];
f = ChainVar[5];
g = ChainVar[6];
h = ChainVar[7];
for (j = 0; j < 64; j += 8)
{
FF(a, b, c, d, e, f, g, h, j + 0);
FF(h, a, b, c, d, e, f, g, j + 1);
FF(g, h, a, b, c, d, e, f, j + 2);
FF(f, g, h, a, b, c, d, e, j + 3);
FF(e, f, g, h, a, b, c, d, j + 4);
FF(d, e, f, g, h, a, b, c, j + 5);
FF(c, d, e, f, g, h, a, b, j + 6);
FF(b, c, d, e, f, g, h, a, j + 7);
}
ChainVar[0] += a;
ChainVar[1] += b;
ChainVar[2] += c;
ChainVar[3] += d;
ChainVar[4] += e;
ChainVar[5] += f;
ChainVar[6] += g;
ChainVar[7] += h;
총 64번의 셔플을 진행한다.
