2293. 동전1
문제
n가지 종류의 동전이 있다. 각각의 동전이 나타내는 가치는 다르다. 이 동전을 적당히 사용해서, 그 가치의 합이 k원이 되도록 하고 싶다. 그 경우의 수를 구하시오. 각각의 동전은 몇 개라도 사용할 수 있다.
사용한 동전의 구성이 같은데, 순서만 다른 것은 같은 경우이다.
입력
첫째 줄에 n,k가 주어진다. (1<=n<=100, 1<=k<=10,000) 다음 n개의 줄에는 각각의 동전의 가치가 주어진다. 동전의 가치는 100,000보다 작거나 같은 자연수이다.
출력
첫째 줄에 경우의 수를 출력한다. 경우의 수는 2^31보다 작다.
풀이
완전탐색으로 풀 경우,
시간초과가 발생한다.(시간제한이0.5초이기 때문이다.)
때문에 DP를 사용할 필요가 있다. DP를 어떻게 활용할 수 있을까?
구해야 하는 값은 합이 k가 되는 경우의 수이다. 그렇다면 0부터 k까지의 수를 n(0 <= n <= k)이라고 하자. 주어진 수(동전의 가치)를 더해서 각각의 n을 만들 수 있는 경우의 수를 구해나가면 최종적으로 k를 만들 수 있는 경우의 수를 구할 수 있다.
예를 들어, nums = [1,2,5], k = 10 의 경우
1. 1로 0 ~ 10(k)를 만들 수 있는 경우의 수를 DP 배열로 표현하면 아래 그림과 같다.

2. 현재 DP 상태에서 2로 0 ~ 10(k)를 만들 수 있는 경우의 수들을 어떻게 DP에 표현할 수 있을까?
- 먼저 2보다 작은 수들은 2가 포함된 합으로는 표현할 수 없으므로 넘어간다.
- dp[2] : 숫자 2를 합으로 만들 수 있는 경우의 수를 의미한다.
2을 만들 수 있는 경우의 수는 1에서 1를 더하거나(이 결과는 현재 dp[2]와 동일하다.) 0에서 2를 더하면 된다(이 결과는 0을 만드는 경우의 수와 동일함을 알 수 있다. 0을 만드는 조합에서 마지막에 2만 추가된 것이기 때문이다.).
즉, dp[2] = dp[2] + dp[0]이 된다.
3. dp[3]도 동일하다. 1과 2를 활용해서 3을 만들 수 있는 경우의 수는
- 2를 사용하지 않고 기존의 숫자들로만 3을 만드는 경우의 수 : dp[3]
- 3에서 2를 뺀 숫자(1)를 만들 수 있는 조합에 2만 추가하는 경우, 이 때 경우의 수는 3에서 2를 뺀 숫자(1)과 동일하기 때문에 : dp[1]이다.
- 즉, dp[3] = dp[3] + dp[1]
4. 이런 순서로 1과 2를 활용해 1 ~ 10(k)까지의 수를 만드는 경우의 수는 아래 그림과 같다.
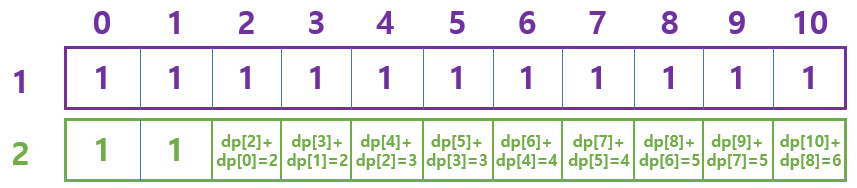
5. 그럼 마지막 수인 5까지 사용한 경우의 수는 어떻게 구할까? 2와 동일하다. 1 ~ k까지의 수(n)에서
- 5를 사용하지 않는 경우의 수(dp[n]) + 5를 뺀 수(k-5)를 만들 수 있는 경우의 수(dp[n-5])와 동일함을 알 수 있다.
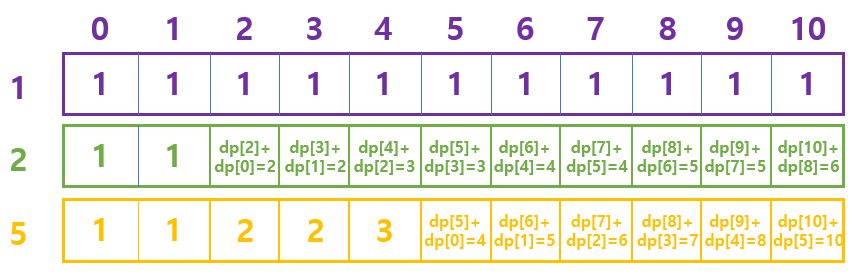
즉, nums의 각 원소를 num이라 할 때, dp[n] = dp[n] + dp[n-nums]인 것을 알 수 있다.
코드
n, k = map(int, input().split())
nums = [ int(input()) for _ in range(n) ]
dp = [0 for _ in range(k+1)]
dp[0] = 1
for num in nums :
for i in range(1, k+1) :
if i - num >= 0 :
dp[i] += dp[i-num]
print(dp[k])마치며
역시 아직 DP 문제를 푸는데 시간이 많이 소요되고 있다. DP 문제와 관련해서는 많이 풀어보고, 복습하자.
