167. Two Sum II - Input Array Is Sorted

Problem

Given a 1-indexed array of integers numbers that is already sorted in non-decreasing order, find two numbers such that they add up to a specific target number. Let these two numbers be numbers[index1] and numbers[index2] where 1 <= index1 < index2 <= numbers.length.

Return the indices of the two numbers, index1 and index2, added by one as an integer array [index1, index2] of length 2.

The tests are generated such that there is exactly one solution. You may not use the same element twice.

Example 1:

Input: numbers = [2,7,11,15], target = 9
Output: [1,2]
Explanation: The sum of 2 and 7 is 9. Therefore, index1 = 1, index2 = 2. We return [1, 2].

Example 2:

Input: numbers = [2,3,4], target = 6
Output: [1,3]
Explanation: The sum of 2 and 4 is 6. Therefore index1 = 1, index2 = 3. We return [1, 3].

Example 3:

Input: numbers = [-1,0], target = -1
Output: [1,2]
Explanation: The sum of -1 and 0 is -1. Therefore index1 = 1, index2 = 2. We return [1, 2].

Constraints:

• 2 <= numbers.length <= 3 * 104
• -1000 <= numbers[i] <= 1000
• numbers is sorted in non-decreasing order.
• -1000 <= target <= 1000
• The tests are generated such that there is exactly one solution.

풀이

Two Point를 사용해 풀 수 있다.

• 주어진 배열이 정렬되어 있으며, 두 개의 수를 이용해 target을 구한다는 점에 유의하자.

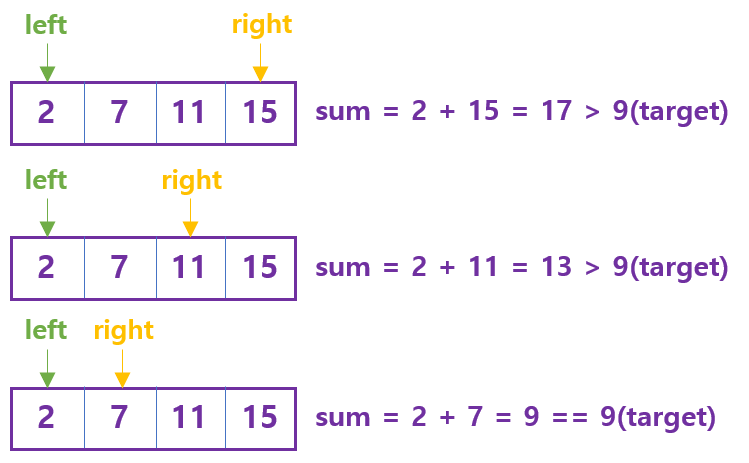
• 가장 작은 수(index 0)와 가장 큰 수(index -1)를 더한 결과 값을 sum이라 할 때, sum이 target 보다 작으면 어떻게 해야 할까? sum에는 더 큰 수를 더해줄 필요가 있다. 따라서 가장 작은 수(index 0)보다 다음으로 작은 수(index 1)을 가장 큰 수(index -1)과 더해주면 sum은 target에 더 가까이 갈 수 있을 것이다.

• 반대로, sum이 target보다 클 경우에는 어떻게 해야 할까? sum에는 가장 큰수 (index -1)보다 작은 수를 더해줄 필요가 있으므로, index -1 다음으로 큰 수인 index -2와 가장 작은 수(index 0)를 더해주면 sum은 target에 더 가까워질 수 있다.

• 따라서, 아래와 같으 구현할 수 있다.

  left, right = 0, len(nums) - 1
  sum = nums[left] + nums[right]
  if sum == 0 : return
  elif sum < 0 : left++
  else : right--

• Ex) numbers = [2,7,11,15], target = 9
  

코드

class Solution(object):
    def twoSum(self, numbers, target):
        """
        :type numbers: List[int]
        :type target: int
        :rtype: List[int]
        """
        left = 0
        right = len(numbers) - 1
        
        while left < right :
            sum = numbers[left] + numbers[right]
            
            if sum == target :
                return [left+1,right+1]
            elif sum < target :
                left += 1
            else :
                right -= 1