[프로그래머스] 합승 택시 요금

문제

정확성과 효율성 테스트

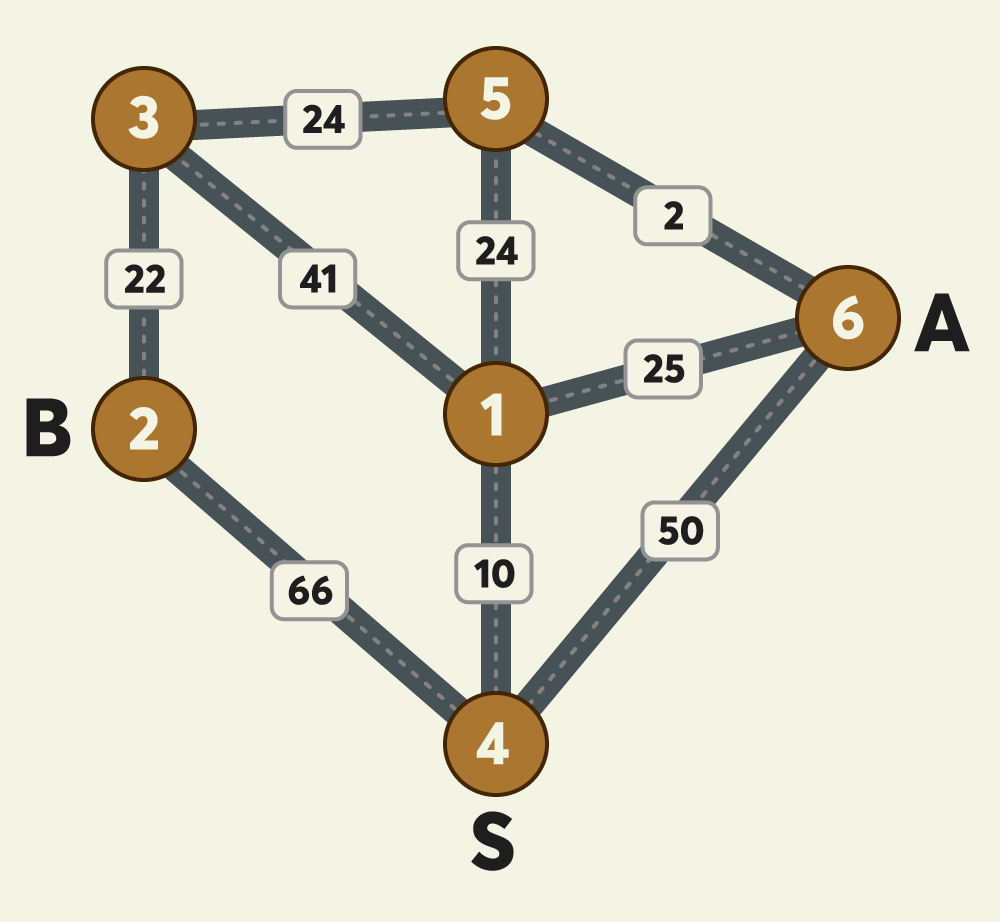
지점의 개수 n, 출발지점을 나타내는 s, A의 도착지점을 나타내는 a,B의 도착지점을 나타내는 b, 지점 사이의 예상 택시요금을 나타내는 fares가 매개변수로 주어집니다. 이때, A,B 두 사람이 s에서 출발해서 각각의 도착 지점까지 택시를 타고 간다고 가정할 때, 최저 에상 택시요금을 계산해서 return 하도록 solution 함수를 완성해주세요.
만약, 아예 합승을 하지 않고 각자 이동하는 경우의 예상 택시요금이 낮다면, 합승을 하지 않아도 됩니다.

제한사항

• 지점갯수 n은 3이상 200이하인 자연수입니다.
• 지점 s,a,b는 1이상 n 이하인 자연수이며, 각기 서로 다른 값입니다.
• fares는 2차원 정수 배열입니다.
  • fared 배열의 각 행은 [c,d,f] 형태입니다.
  • c지점과 d지점 사이의 예상 택시요금이 f원이라는 뜻입니다.
• 출발지점 s에서 도착지점 a와 b로 가는 경로가 존재하는 경우만 입력으로 주어집니다.

풀이

문제에서 주어진 이미지만 봐도 알 수 있듯이 그래프 문제입니다.
먼저 플로이드 와샬 알고리즘을 사용하여 모든 노드들 간의 최소 거리를 찾아줍니다.

    for k in range(n):
        for i in range(n):
            for j in range(n):
                if board[i][k] + board[k][j] < board[i][j]:
                    board[i][j] = board[i][k] + board[k][j]

1~n 까지의 지점을 경유지로 보았을 때의 소요되는 금액의 최소값을 정하면 됩니다.

    answer = board[s][a] + board[s][b]
    for e in range(n):
        answer = min(answer, board[s][e]+board[e][a]+board[e][b])

이 때, 경유지를 들리지 않고(합승하지 않고) 바로 a,b로 이동하였을 경우의 택시요금이 초기값입니다.

코드

def solution(n, s, a, b, fares):
    INF = int(1e9)
    board = [[INF] * n for _ in range(n)]
    
    for c,d,f in fares:
        board[c-1][d-1] = board[d-1][c-1] = f
    for i in range(n):
        board[i][i] = 0
        
    for k in range(n):
        for i in range(n):
            for j in range(n):
                if board[i][k] + board[k][j] < board[i][j]:
                    board[i][j] = board[i][k] + board[k][j]
    
    s,a,b = s-1,a-1,b-1
    answer = board[s][a] + board[s][b]
    for e in range(n):
        answer = min(answer, board[s][e]+board[e][a]+board[e][b])
    return answer