Lv.4 올바른 괄호의 갯수

문제 설명

자료 구조

• Molecular
  • 타입 : 정수
  • 저장 데이터 : 분자로 쓸 변수
• denominator
  • 타입 : 정수
  • 저장 데이터 : 분모로 쓸 변수

풀이 과정

• 3 x n 타일링 문제와 같은 원리

일반식을 추측하기 위해 초반 항 몇 가지를 구한다.

f(1) = 1, f(2) = 2 , f(3) = 5, f(4) = 14...
f(1) = ( )
f(2) = ( ) ( ), ( ( ) )

• ()()는 f(1)에서 괄호 한 쌍을 추가하면 만들 수 있다.
• 하지만 (())는 f(1)의 괄호 뒤에 추가하는 방법으로는 만들 수 없다.
  • 옆에 추가하는 방식으로는 못 만드는, 괄호 2쌍을 순전히 채우는 경우를 g(2)로 칭하겠다.

-> f(3) = f(1)에서 2쌍을 채운다 + f(2)에서 1쌍을 채운다 + g(3).
-> f(4) = f(1)에서 3쌍을 채운다 + f(2)에서 2쌍을 채운다 + f(3)에서 한 쌍을 채운다 + g(4)

...

이를 식으로 정리하면 아래와 같다.

f(3) = g(3) + f(1) * g(2) + f(2) * g(1) + g(3)
f(4) = g(4) + f(1) * g(3) + f(2) * g(2) + f(3) * g(1)
f(5) = g(5) + f(1) * g(4) + f(2) * g(3) + f(3) * g(2) + f(4) * g(1)
...
f(n) = g(n) + f(1) * g(n-1) + f(2) * g(n-2) + ... f(i) * g(n-i) + ... + f(n-1) * g(1) 

• g(n)의 규칙성을 찾자.

g(1) = ( )
g(2) = ( ( ) )
g(3) = ( ( ( ) ) ), ( ( ) ( ) ),
g(4) = ( ( ) ( ( ) ) ), ( ( ) ( ) ( ) ), ( ( ( ) ) ( ) ), ( ( ( ( ) ) ) ), ( ( ( ) ( ) ) )
...

( ) 안에 n-1쌍의 괄호를 만들고 있다.
n-1쌍의 괄호를 만드는 경우의 수는 f(n-1)이다.
즉, g(n) = f(n-1)이므로 일반항은 아래와 같이 정리된다.

f(n) = f(n-1) * f(1) + f(n-2) * f(2) + ... +  f(1) * f(n-1)

이는 아래 그림과 같이 정리된다.

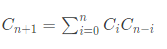
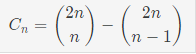
코드 구현(JavaScript)

function solution(n) {
	let Molecular = n + 1, denominator = n;
        
	for (let i = 1; i < n; i++) {
        Molecular *= n + 1 + i; 
        denominator *= n - i;
   }
	return Number(Molecular / denominator) / (n + 1);
}

출처: 프로그래머스