[백준] 1167번-(Python 파이썬) - Tree, dfs, bfs, Dijkstra

문제링크 : https://www.acmicpc.net/problem/1167

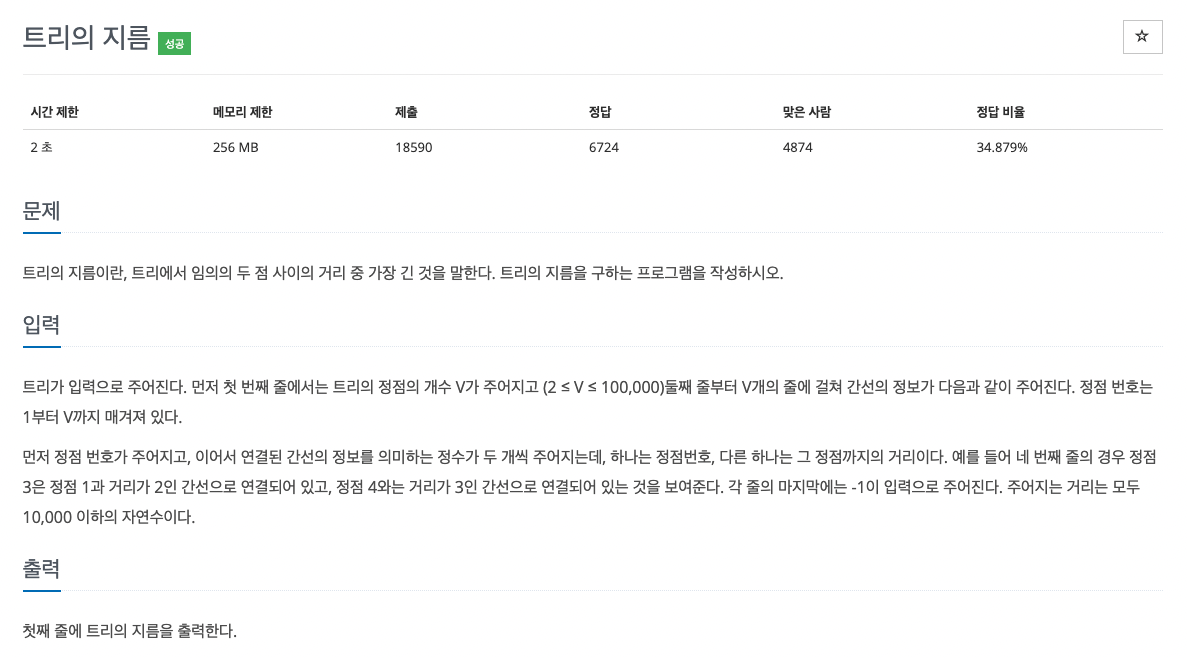
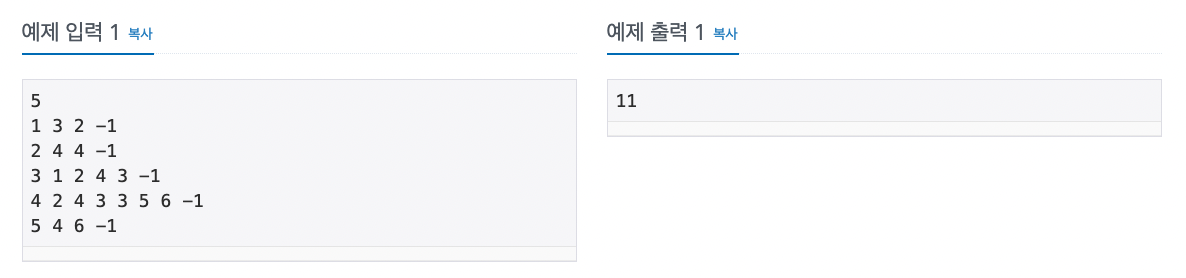
이번 문제는 bfs알고리즘을 이용해 푼 풀이와 dijkstra를 이용한 두 가지 풀이가 있다.
처음 코드는 서로 연결되어있는 그래프에서 bfs나 dfs로 아무 노드에서 가장 멀리 있는 노드를 구한 뒤,
가장 멀리 있는 노드에서 한번더 가장 멀리 있는 노드를 구하면 된다.

import sys
from collections import deque
input = sys.stdin.readline

v = int(input())
graph = [[] for _ in range(v + 1)]
for _ in range(v):
  a = list(map(int, input().split()))
  for i in range(1, len(a) -2, 2):
    graph[a[0]].append([a[i], a[i + 1]])
 
def bfs(start):
  visit = [-1] * (v + 1)
  q = deque()
  q.append(start)
  visit[start] = 0
  max_ = [0, 0]

  while q:
    temp = q.popleft()
    for i, j in graph[temp]:
      if visit[i] == -1:
        visit[i] = visit[temp] + j
        q.append(i)
        if max_[0] < visit[i]:
          max_ = visit[i], i

  return max_

dis, node = bfs(1)
dis, node = bfs(node)
print(dis) 

다익스트라 알고리즘을 이용한 풀이는 위에 코드와 똑같이 아무 노드에서 가장 멀리있는 노드의 가중치를 구한뒤 그 가중치의 인덱스를 이용해 가장 멀리 있는 노드의 값을 구한다. 그 가장 멀리 있는 노드를 이용해 한번 더 가장 멀리있는 노드의 가중치를 구하면 된다.

from heapq import heappush, heappop
import sys

input = sys.stdin.readline
inf = sys.maxsize

def dijkstra(start):
    heap = []
    heappush(heap, [0, start])
    dp = [inf for _ in range(v + 1)]
    dp[start] = 0
    while heap:
        w, n = heappop(heap)
        for n_n, wei in graph[n]:
            n_w = wei + w
            if n_w < dp[n_n]:
                dp[n_n] = n_w
                heappush(heap, [n_w, n_n])
    
    return dp

v = int(input())
graph = [[] for _ in range(v + 1)]

for _ in range(v):
    a = list(map(int, input().split()))
    for i in range(1, len(a)-2, 2):
        graph[a[0]].append([a[i], a[i + 1]])

d = dijkstra(1)
f_node = d.index(max(d[1:]))
d_ = dijkstra(f_node)
ans = max(d_[1:])
print(ans)