[백준] 10254 - 고속도로 (java)

HaYeong Jang·2021년 1월 19일

ccw convex-hull rotating calipers 백준 알고리즘

[백준] 알고리즘

목록 보기

12/62

문제

n개의 도시를 가진 나라가 있다. 이 나라에서는 도시들 중 가장 먼 두 도시 사이에 직행 고속도로를 놓으려 한다.

고속도로는 시작점과 끝점이 아닌 다른 나라를 통과해도 된다. 즉, n개의 도시 중 유클리드 거리가 가장 먼 두 도시를 찾으려 한다. 모든 도시는 한 평면 위에 있다.

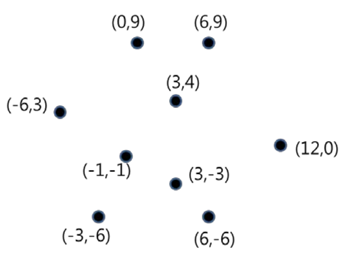
위의 예제에서는 (12,0)의 도시와 (-6,3)의 도시가 가장 먼 유클리드 거리를 갖는다.

도시 n개의 좌표가 주어지면 모든 두 도시 쌍의 거리 중 가장 먼 두 도시를 찾아라.

입력

첫째 줄에 테스트 케이스의 수 T가 주어진다.

각 테스트 케이스의 첫 줄엔 도시의 개수 n이 주어진다. (2 ≤ n ≤ 200,000) 그 후 n줄에 걸쳐 각 도시의 x좌표와 y좌표가 주어진다. (-10,000,000 ≤ x, y ≤ 10,000,000) x, y는 항상 정수이며, 어떤 두 도시가 같은 점 위에 있는 경우는 없다.

출력

테스트 케이스마다 가장 먼 두 점의 좌표를 출력한다.

만일 그 두 점의 좌표가 각각 (x1, y1), (x2, y2)이라면 x1 y1 x2 y2를 출력하면 된다.

가장 먼 거리를 갖는 두 점의 쌍이 여러 개라면 그 중 아무 것이나 출력해도 상관없다.

예제 입력

예제 출력

-100 -50 100 50
-6 3 12 0

코드

import java.io.*;
import java.util.*;

class Point {
    long x, y;

    Point(long x, long y) {
        this.x = x;
        this.y = y;
    }
}

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int T = Integer.parseInt(st.nextToken());    // 테스트 케이스
        ArrayList<Point> points = new ArrayList<>();

        for (int test = 0; test < T; test++) {
            st = new StringTokenizer(br.readLine());
            int n = Integer.parseInt(st.nextToken());    // 도시의 개수
            points.clear();

            for (int i = 0; i < n; i++) {
                st = new StringTokenizer(br.readLine());
                long x = Long.parseLong(st.nextToken());
                long y = Long.parseLong(st.nextToken());

                points.add(new Point(x, y));
            }

            ArrayList<Point> list = new ArrayList<>(convexHull(points));
            Point[] result = rotatingCalipers(list);

            bw.write(result[0].x + " " + result[0].y + " " + result[1].x + " " + result[1].y + "\n");
        }
        br.close();
        bw.flush();
        bw.close();
    }

    static Point[] rotatingCalipers(ArrayList<Point> convexHull) {
        double max_dist = 0;
        Point[] point_pair = new Point[2];

        int j = 1;
        for (int i = 0; i < convexHull.size(); i++) {
            int i_next = (i + 1) % convexHull.size();
            for (; ; ) {
                int j_next = (j + 1) % convexHull.size();

                long bx = convexHull.get(i_next).x - convexHull.get(i).x; // 왼쪽 벡터
                long by = convexHull.get(i_next).y - convexHull.get(i).y;
                long cx = convexHull.get(j_next).x - convexHull.get(j).x;   // 오른쪽 벡터
                long cy = convexHull.get(j_next).y - convexHull.get(j).y;

                long ccw = ccw(new Point(0, 0), new Point(bx, by), new Point(cx, cy));
                if (ccw > 0) {  // 반시계 방향이면 오른쪽에 있는 점을 다음으로
                    j = j_next;
                } else {    // 시계 방향이면 왼족에 있는 점을 다음으로
                    break;
                }
            }

            // 최대 거리 구하기
            if (dist(convexHull.get(i), convexHull.get(j)) > max_dist) {
                max_dist = dist(convexHull.get(i), convexHull.get(j));
                point_pair[0] = convexHull.get(i);
                point_pair[1] = convexHull.get(j);
            }
        }

        return point_pair;
    }

    static Stack<Point> convexHull(ArrayList<Point> input) {
        Point root = new Point(Long.MAX_VALUE, Long.MAX_VALUE);

        // 기준점 찾기
        for (int i = 0; i < input.size(); i++) {
            if (input.get(i).x < root.x) {
                root = input.get(i);
            } else if (input.get(i).x == root.x) {
                if (input.get(i).y < root.y) {
                    root = input.get(i);
                }
            }
        }

        // 모든 점들을 반시계 방향으로 정렬하기
        Point finalRoot = root;
        input.sort(new Comparator<Point>() {
            @Override
            public int compare(Point o1, Point o2) {
                long ccw = ccw(finalRoot, o1, o2);

                if (ccw > 0) {
                    return -1;
                } else if (ccw < 0) {
                    return 1;
                } else {
                    double distance1 = dist(finalRoot, o1);
                    double distance2 = dist(finalRoot, o2);

                    return Double.compare(distance1, distance2);
                }
            }
        });

        Stack<Point> stack = new Stack<>();
        stack.add(root);

        for (int i = 1; i < input.size(); i++) {
            while (stack.size() > 1 && (ccw(stack.get(stack.size() - 2), stack.get(stack.size() - 1), input.get(i)) <= 0)) {
                stack.pop();
            }
            stack.add(input.get(i));
        }

        return stack;
    }

    static long ccw(Point p1, Point p2, Point p3) {
        return (p1.x * p2.y + p2.x * p3.y + p3.x * p1.y) - (p1.y * p2.x + p2.y * p3.x + p3.y * p1.x);
    }

    static double dist(Point p1, Point p2) {
        return Math.sqrt((p2.x - p1.x) * (p2.x - p1.x) + (p2.y - p1.y) * (p2.y - p1.y));
    }
}