[PCCP] 그리디 알고리즘 - 선 긋기 | 파이썬

코딩테스트 역량 강화 교육(거점형 특화 프로그램)이라는 프로그램에 참여해 공부한 내용입니다.

• IT 직무로 취업을 희망하는 지원자들이 코딩테스트를 통과할 수 있는 알고리즘을 활용한 프로그래밍 교육이며, PCCP 자격증 취득이 목표인 프로그램
• 상세 설명 - 수원대학교(대학일자리 플러스센터)

---

그리디 알고리즘 - 선 긋기

앞서 공부한 그리디 알고리즘을 사용해 선 긋기 문제를 풀어보겠다.

---

문제

한 번의 선긋기는 수직선상의 한 점에서 다른 한 점까지 선을 긋는 것입니다.
선을 그을 때는 이미 선이 있는 위치에 겹쳐서 그을 수도 있습니다.
여러번 그은 곳과 한 번 그은 곳의 차이는 없습니다.
수직선은 0번 지점부터 m번 지점까지의 길이를 갖고 있습니다.
매개변수 nums에 각각의 선긋기 정보가 주어지면 0번 지점부터 m번 지점까지 연속적인 선이 그어지도록 하기 위한 선긋기 최소횟수를 반환하는 프로그램을 작성하세요.
모든 입력은 0번 지점부터 m번지점까지 연속적인 선이 그어집니다.

---

입출력 예

box	limit	answer
12	[[5, 10], [1, 8], [0, 2], [0, 3], [2, 5], [2, 6], [10, 12], [7, 12]]	3
15	[[1, 10], [0, 8], [0, 7], [0, 10], [12, 5], [0, 12], [8, 15], [5, 14]]	2
20	[[3, 7], [5, 8], [15, 20], [0, 5], [7, 14], [3, 10], [0, 8], [13, 18], [5, 9]]	4
30	[[5, 7], [3, 9], [2, 7], [0, 1], [0, 2], [0, 3], [19, 30], [8, 15], [7, 12], [13, 20]]	5
25	[[10, 15], [15, 20], [5, 15], [3, 16], [0, 5], [0, 3], [12, 25]]	3

예제 1번 설명

---

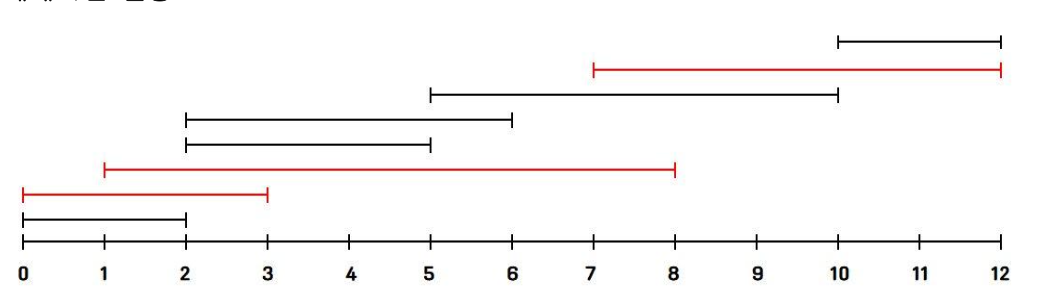
제한사항

• 3 <= m <= 10,000
• nums의 길이는 100,000을 넘지 않습니다.
• nums[i][0]은 i번째 선긋기의 시작 점, nums[i][1]은 i번째 선긋기의 끝점입니다.
• 0 <= nums[i][0] < nums[i][1] <= 10,000

---

코드

def solution(m, nums):
    answer = 0
    n = len(nums)
    
    # 시작점을 기준으로 정렬
    nums.sort(key= lambda x: x[0])

    # start : 시작점, end : 현재 위치
    start = end = i = 0

    while i < n:
        # i번째 선이 start보다 작거나 같은 선들만 봄
        while i < n and nums[i][0] <= start:
            # 그중에 가장 멀리가는 선을 찾음
            end = max(end, nums[i][1])
            # 처리했다면 다음 선으로 넘어감
            i += 1
        
        # 선을 찾았으니 긋고 횟수 + 1
        answer += 1
  
		start = end
        
        if end == m:
           return answer
        

    return answer
    
                                           
print(solution(12, [[5, 10], [1, 8], [0, 2], [0, 3], [2, 5], [2, 6], [10, 12], [7, 12]]))
print(solution(15, [[1, 10], [0, 8], [0, 7], [0, 10], [5, 12], [0, 12], [8, 15], [5, 14]]))
print(solution(20, [[3, 7], [5, 8], [15, 20], [0, 5], [7, 14], [3, 10], [0, 8], [13, 18], [5, 9]]))
print(solution(30, [[5, 7], [3, 9], [2, 7], [0, 1], [0, 2], [0, 3], [19, 30], [8, 15], [7, 12], [13, 20]]))
print(solution(25, [[10, 15], [15, 20], [5, 15], [3, 16], [0, 5], [0, 3], [12, 25]]))

---

풀이

이 문제는 선이 이어지도록 현재 start보다 작거나 같으면서, end가 가장 큰 선을 찾는 게 중요하다.

1. 먼저 시작점 x[0]을 기준으로 오름차순 정렬
2. start, end, i은 0으로 초기화
3. while문을 통해 start보다 적거나 같고, i가 nums의 인덱스를 벗어나지 않는 선들만 찾아서 그 중 끝 점 end가 가장 큰 선을 찾아 end로 저장
4. 앞서 while문을 통해 선을 하나 그었으니 answer += 1을 하고 다음 시작점을 end로 지정
5. 만약 i가 nums의 인덱스를 벗어나거나 end과 m이 동일하다면 선을 다 그은 것이므로 return answer