
다익스트라 알고리즘
다익스트라 알고리즘: 음의 가중치(음의 간선이나 값)가 없는 그래프의 한 노드에서 각 모든 노드까지의 최단 거리를 구하는 알고리즘
초기엔 O(V²)의 시간복잡도를 가졌지만, 현재는 우선순위 큐 등을 이용하여 O((V+E)logV)의 시간 복잡도를 가지며, 만약 연결 그래프라면 O(ElogV)까지 시간 복잡도를 줄일 수 있고, 일반적으로 희소그래프인 경우 우선순위 큐를 이용하는 것이 낫다고 한다.
연결 그래프: 모든 두 꼭짓점 사이에 경로가 존재하는 그래프밀집 그래프: 간선의 수가 최대에 가까운 그래프를 말하며 보통, 간선의 총 개수가(정점의 개수)²과 근사하다면 밀집 그래프에 해당희소 그래프: 밀집 그래프의 반대
다익스트라 알고리즘의 매커니즘
다익스트라 알고리즘은 기본적으로 그리디와 다이나믹 프로그래밍을 사용한 알고리즘이다.
임의의 노드에서 다른 노드로 가는 값을 비용이라고 하며, 기본적으로 아래 두 단계를 반복해 임의의 노드에서 각 모든 노드까지의 최단 거리를 구한다.
1. 방문하지 않은 노드 중 가장 비용이 적은 노드를 선택 -> 그리디 알고리즘
2. 해당 노드로부터 갈 수 있는 노드들의 비용을 갱신 -> 다이나믹 프로그래밍
예시
예를 들어 A노드에서 출발해서 F노드로 가는 최단 경로를 구한다고 생각해보자.
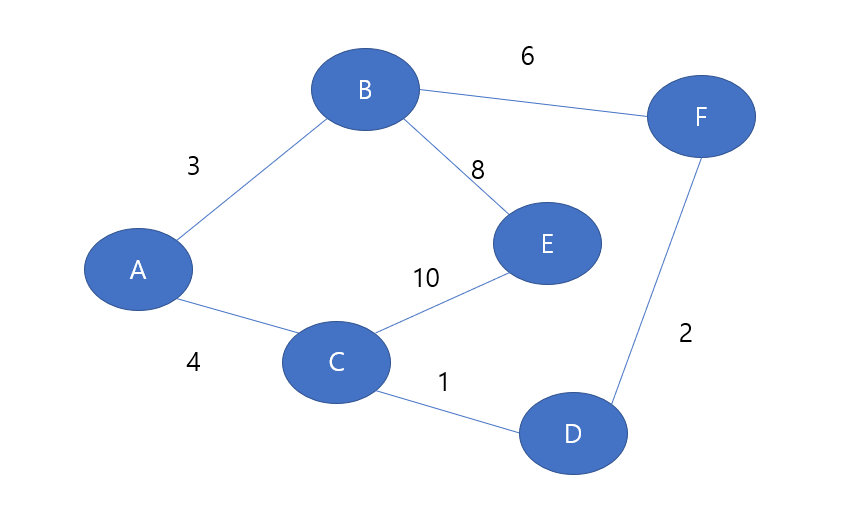
또, 각 단계별로 방문 표시를 할 ch 리스트와 현재까지 A노드가 방문한 곳까지의 최소 비용을 dist[대상노드]라고 정의했다.

여기서 ?는 Integer.MAX_VALUE라고 생각하자.
1. 초기화 단계
첫 번째 단계에서는 가장 비용이 적은 노드를 선택할 기준이 없기 때문에 출발지인 A노드 자신을 초기 선택 노드로 초기화한다.
즉, A노드에서 A노드는 비용이 0이므로 0으로 설정한다.

2. A 방문
초기화가 끝났으니 이제 메커니즘에서 설명한 두 단계를 노드들을 반복해서 적용하면 된다.
현재 방문하지 않은 노드 중 가장 비용이 적은 노드인 A노드를 기준으로, 갈 수 있는 인접 노드로의 최소 비용은 아래와 같다.

3. B 방문
방문하지 않은 노드 중 가장 비용이 적은 노드가 B 노드이므로 B노드에서 인접 노드로의 최소 비용을 구해보자.
A노드와 겹치는 노드가 없으니 E, F 노드의 값만 새로 갱신됐다.

4. C 방문
방문하지 않은 노드 중 가장 비용이 적은 노드가 C 노드이므로 C 노드에서 인접 노드로의 최소 비용을 구해보자.
D노드는 갱신되지 않았으므로 A->C->D의 비용을 합친 값으로 갱신해주고,
E노드는 기존 최소 비용인 9와 A->C->E로의 비용인 14를 비교해 작은 값인 기존 값 9를 그대로 저장한다.

5. D 방문
방문하지 않은 노드 중 가장 비용이 적은 노드가 D 노드이므로 D 노드에서 인접 노드로의 최소 비용을 구해보자.
F노드는 기존 최소 비용인 11과 A->C->D->F로의 비용인 7를 비교해 작은 값인 7를 새로 갱신한다.

6. F 방문
방문하지 않은 노드 중 가장 비용이 적은 노드가 F 노드이지만, 갱신할 값이 없으므로 아무 동작없이 넘어간다.

7. E 방문
마지막으로 방문하지 않은 노드 중 가장 비용이 적은 노드가 E 노드이지만, 갱신할 값이 없으므로 아무 동작없이 넘어가며, dist 배열 각각의 원소에 해당 노드로 가는 최소 비용이 저장된다.

O(V²) 코드
먼저 코드를 보기 전에 입력으로 주어진 그래프를 저장하는 방법에 익숙하지 않다면 [알고리즘] 그래프(Graph) 게시물을 참고하면 좋다.
import java.util.*;
class Node {
int idx;
int cost;
Node(int idx, int cost) {
this.idx = idx;
this.cost = cost;
}
}
public class Dijkstra {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int V = sc.nextInt(); // 정점 수
int E = sc.nextInt(); // 간선 수
int start = sc.nextInt(); // 출발 지점
// 그래프 초기화
ArrayList<ArrayList<Node>> graph = new ArrayList<ArrayList<Node>>();
for (int i = 0; i < V + 1; i++) graph.add(new ArrayList<>());
// 그래프에 값 입력
for (int i = 0; i < E; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int cost = sc.nextInt();
graph.get(a).add(new Node(b, cost));
}
// 확인 및 최소 비용 배열 초기화
boolean[] ch = new boolean[V + 1];
int[] dist = new int[V + 1];
// 최대값으로 설정(위에서 ?를 의미)
for (int i = 0; i < V + 1; i++) dist[i] = Integer.MAX_VALUE;
// 출발지점 비용 0으로 초기화 단계
dist[start] = 0;
// 다익스트라 알고리즘 시작
for (int i = 0; i < V; i++) {
int nodeValue = Integer.MAX_VALUE;
int nodeIdx = 0;
// 방문하지 않은 노드 중 최소 비용 찾기
for (int j = 1; j < V + 1; j++) {
if (!ch[j] && dist[j] < nodeValue) {
nodeValue = dist[j];
nodeIdx = j;
}
}
// 최소비용 노드를 찾아 방문 처리
ch[nodeIdx] = true;
// 최소 비용 노드에서 인접한 노드들 중
// 현재 선택된 노드의 값(dist[adjNode.idx])보다,
// 현재 노드에서 인접 노드로 가는 값(dist[nodeIdx] + adjNode.cost)을 비교해
// 더 작은 값으로 갱신
for (int j = 0; j < graph.get(nodeIdx).size(); j++) {
Node adjNode = graph.get(nodeIdx).get(j);
if (dist[adjNode.idx] > dist[nodeIdx] + adjNode.cost) {
dist[adjNode.idx] = dist[nodeIdx] + adjNode.cost;
}
}
}
// 최종 비용 출력
System.out.println(Arrays.toString(dist));
sc.close();
}
}이 코드의 경우 최악의 경우 모든 노드들을 확인해야하며, 이것을 V번 반복하기 때문에 O(V²)의 시간 복잡도를 가진다.
O((V+E)logV) 코드
위에서 최소 비용을 갖는 노드를 선택하고, 그 노드의 인접 노드 값을 갱신했다.
즉, 갱신하는 주변 노드의 값에 대해서만 다음 최소 비용을 갖는 노드를 선택해주면 된다는 것이 우선순위 큐를 이용하는 것의 핵심이다.
import java.util.*;
public class DijkstraQueue {
static ArrayList<ArrayList<Node>> graph;
static int[] dist;
static int V;
static class Node {
int idx, cost;
Node(int idx, int cost) {
this.idx = idx;
this.cost = cost;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int V = sc.nextInt(); // 정점 수
int E = sc.nextInt(); // 간선 수
int start = sc.nextInt(); // 출발 지점
// 그래프 초기화
ArrayList<ArrayList<Node>> graph = new ArrayList<ArrayList<Node>>();
for (int i = 0; i <= V; i++) graph.add(new ArrayList<>());
// 그래프에 값 입력
for (int i = 0; i < E; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int cost = sc.nextInt();
graph.get(a).add(new Node(b, cost));
}
// 최소 비용 배열 초기화
int[] dist = new int[V+1];
Arrays.fill(dist, Integer.MAX_VALUE);
// 다익스트라 메소드 호출
dijkstra(start);
System.out.println(Arrays.toString(dist));
}
public static void dijkstra(int s) {
// 우선순위 큐(Node 객체의 cost를 기준으로 오름차순 정렬)
PriorityQueue<Node> pq = new PriorityQueue<>(Comparator.comparingInt(o -> o.cost));
// 초기화 단계
pq.add(new Node(s, 0)); // 시작지점 큐에 삽입
dist[s] = 0; // 출발지점 비용 0으로 설정
// 방문 확인 배열 초기화
boolean[] ch = new boolean[V+1];
// 큐가 비어질 때까지 반복
while (!pq.isEmpty()) {
// 현재 최소 비용을 갖는 노드 꺼내기
Node cur = pq.poll();
// 현재 꺼낸 노드가 방문하지 않은 경우
if(!ch[cur.idx]) {
ch[cur.idx] = true; // 방문 표시
// 현재 노드의 인접 노드들 꺼내기
for (Node next : graph.get(cur.idx)) {
// 꺼낸 인접 노드가 방문하지 않았으면서,
// 인접 노드의 비용보다 현재 노드에서 인접 노드로 가는 값이 더 작은 경우
if (!ch[next.idx] && dist[next.idx] > cur.cost + next.cost) {
// dist 배열의 해당 노드의 최소 비용 값 갱신
dist[next.idx] = cur.cost + next.cost;
// 큐에 넣기
pq.offer(new Node(next.idx, dist[next.idx]));
}
}
}
}
}
}방문한 노드의 최소비용이 갱신되지 않는 이유
노드를 꺼낼 때 항상 최소비용을 갖는 노드를 꺼내기 때문에, 최단 거리를 이어 붙여서 최단 거리를 만들게 된다.
즉, 그리디 알고리즘의 최적 부분 구조 조건이 성립하기 때문에
방문한 노드에 또 방문을 한다고 하더라도 방문한 시점의 비용이 최소비용이기 때문에 더이상 갱신이 이루어지지도 않으며, 실행 시간이 더 오래 걸릴 뿐이다.
if(!ch[cur.idx])다익스트라 알고리즘을 실행하는 과정에서 큐에 같은 도착지로 도착하지만 비용이 다른 경로들이 다수 들어갔을 때, 최소 비용 외의 경로들을 무시하고 넘어가기 때문에 성능에 있어서 위 코드가 꼭 필요하다.
| 참고한 글: https://sskl660.tistory.com/59
