코딩테스트 역량 강화 교육(거점형 특화 프로그램)이라는 프로그램에 참여해 공부한 내용입니다.

• IT 직무로 취업을 희망하는 지원자들이 코딩테스트를 통과할 수 있는 알고리즘을 활용한 프로그래밍 교육이며, PCCP 자격증 취득이 목표인 프로그램
• 상세 설명 - 수원대학교(대학일자리 플러스센터)

---

이분 탐색 (Binary Search)

정의

출처 : 나무위키 - 이진 탐색

• 정렬 등과 함께 가장 기초인 알고리즘으로 꼽히는 문제이며, 검색 범위를 줄여 나가면서 원하는 데이터를 검색하는 알고리즘

• 이분 탐색 알고리즘(Binary Search Algorithm)은 컴퓨터과학, 수학 등에서 오름차순으로 정렬된 정수의 리스트를 같은 크기의 두 부분 리스트로 나누고 필요한 부분에서만 탐색하도록 제한하여 원하는 원소를 찾는 알고리즘

• 리스트의 중간 부분에 찾는 원소가 있는지 확인하고, 없으면 위쪽에 있는지 아래쪽에 있는지 판단하여 맨 앞부터 검색하거나 중간부터 검색

• 이분 탐색을 하려면 꼭 정렬이 된 상태여야 한다.

• 원래 O(n)이 걸리는 시간복잡도를 O(logn)으로 줄일 수 있다.

---

예시 문제

설명

nums에 오름차순으로 정렬된 정수 배열이 주어지고, target에 nums배열에서 찾고자 하는 값 이 주어지면 nums배열에서 target의 인덱스 번호를 찾아 반환하는 프로그램을 작성하세요. 인덱스 번호는 0번부터 시작합니다.
target값이 nums에 존재하지 않을 경우 -1를 반환합니다.

입출력 예

nums	target	answer
[2, 5, 7, 8, 10, 15, 20, 24, 25, 30]	8	3
[-3, 0, 2, 5, 8, 9, 12, 15]	0	1
[-5, -2, -1, 3, 8, 9, 12, 17, 23]	2	-1
[3, 6, 9, 12, 17, 29, 33]	3	0
[1, 2, 3, 4, 5, 7, 9, 11, 12, 15, 16, 17, 18]	18	12

예제 1번을 이분탐색으로 8을 찾는 과정

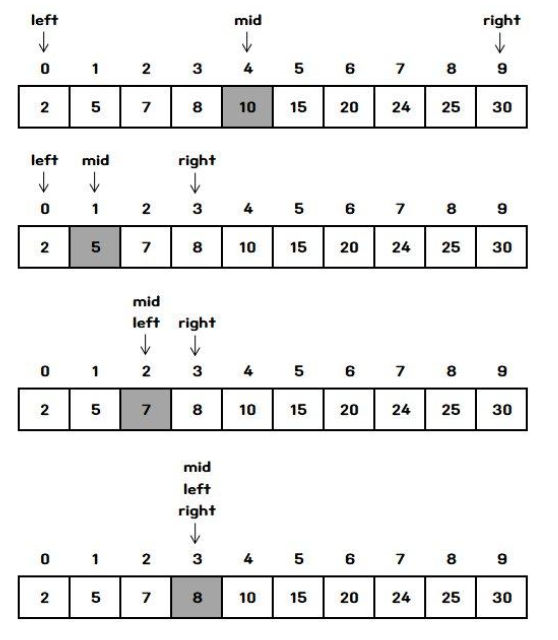
제한사항

• nums의 길이는 100,000,000을 넘지 않습니다. nums의 원소는 유일값입니다.
• -100,000,000 <= nums[i] <= 100,000,000

코드

def solution(nums, target):

    start = 0
    end = len(nums)-1

    while(start <= end):
        mid = (start + end) // 2
        if target == nums[mid]:
            return mid
        elif target < nums[mid]:
            end = mid -1
        else:
            start = mid +1

    return -1
    
                                           
print(solution([2, 5, 7, 8, 10, 15, 20, 24, 25, 30], 8))
print(solution([-3, 0, 2, 5, 8, 9, 12, 15], 0))
print(solution([-5, -2, -1, 3, 8, 9, 12, 17, 23], 2))
print(solution([3, 6, 9, 12, 17, 29, 33], 3))
print(solution([1, 2, 3, 4, 5, 7, 9, 11, 12, 15, 16, 17, 18], 18))

• 정렬이 되어있는 리스트이기 때문에 따로 정렬을 할 필요는 없음
• 먼저 start = 0, end = n-1로 설정(인덱스는 n-1까지)
• start가 end와 같거나 클 때까지 탐색
• num[mid] > target : num[mid] ~ end까진 탐색할 필요 없으므로 end = mid -1
• num[mid] < target : start ~ num[mid]까진 탐색할 필요 없으므로 start = mid + 1