
코딩테스트 역량 강화 교육(거점형 특화 프로그램)이라는 프로그램에 참여해 공부한 내용입니다.
- IT 직무로 취업을 희망하는 지원자들이 코딩테스트를 통과할 수 있는 알고리즘을 활용한 프로그래밍 교육이며, PCCP 자격증 취득이 목표인 프로그램
- 상세 설명 - 수원대학교(대학일자리 플러스센터)
LV.2 - 게임 맵 최단거리
앞서 공부한 BFS(너비 우선 탐색)을 사용해 게임 맵 최단거리 문제를 풀어보겠다.
문제 설명
ROR 게임은 두 팀으로 나누어서 진행하며, 상대 팀 진영을 먼저 파괴하면 이기는 게임입니다. 따라서, 각 팀은 상대 팀 진영에 최대한 빨리 도착하는 것이 유리합니다.
지금부터 당신은 한 팀의 팀원이 되어 게임을 진행하려고 합니다. 다음은 5 x 5 크기의 맵에, 당신의 캐릭터가 (행: 1, 열: 1) 위치에 있고, 상대 팀 진영은 (행: 5, 열: 5) 위치에 있는 경우의 예시입니다.
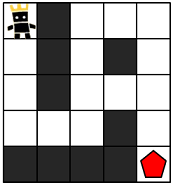
위 그림에서 검은색 부분은 벽으로 막혀있어 갈 수 없는 길이며, 흰색 부분은 갈 수 있는 길입니다. 캐릭터가 움직일 때는 동, 서, 남, 북 방향으로 한 칸씩 이동하며, 게임 맵을 벗어난 길은 갈 수 없습니다.
아래 예시는 캐릭터가 상대 팀 진영으로 가는 두 가지 방법을 나타내고 있습니다.
첫 번째 방법은 11개의 칸을 지나서 상대 팀 진영에 도착했습니다.

두 번째 방법은 15개의 칸을 지나서 상대팀 진영에 도착했습니다.

위 예시에서는 첫 번째 방법보다 더 빠르게 상대팀 진영에 도착하는 방법은 없으므로, 이 방법이 상대 팀 진영으로 가는 가장 빠른 방법입니다.
만약, 상대 팀이 자신의 팀 진영 주위에 벽을 세워두었다면 상대 팀 진영에 도착하지 못할 수도 있습니다. 예를 들어, 다음과 같은 경우에 당신의 캐릭터는 상대 팀 진영에 도착할 수 없습니다.

게임 맵의 상태 maps가 매개변수로 주어질 때, 캐릭터가 상대 팀 진영에 도착하기 위해서 지나가야 하는 칸의 개수의 최솟값을 return 하도록 solution 함수를 완성해주세요. 단, 상대 팀 진영에 도착할 수 없을 때는 -1을 return 해주세요.
제한사항
- maps는 n x m 크기의 게임 맵의 상태가 들어있는 2차원 배열로, n과 m은 각각 1 이상 100 이하의 자연수입니다.
- n과 m은 서로 같을 수도, 다를 수도 있지만, n과 m이 모두 1인 경우는 입력으로 주어지지 않습니다.
- maps는 0과 1로만 이루어져 있으며, 0은 벽이 있는 자리, 1은 벽이 없는 자리를 나타냅니다.
- 처음에 캐릭터는 게임 맵의 좌측 상단인 (1, 1) 위치에 있으며, 상대방 진영은 게임 맵의 우측 하단인 (n, m) 위치에 있습니다.
입출력 예
| maps | answer |
|---|---|
| [[1,0,1,1,1],[1,0,1,0,1],[1,0,1,1,1],[1,1,1,0,1],[0,0,0,0,1]] | 11 |
| [[1,0,1,1,1],[1,0,1,0,1],[1,0,1,1,1],[1,1,1,0,0],[0,0,0,0,1]] | -1 |
입출력 예 설명
입출력 예 #1
주어진 데이터는 다음과 같습니다.
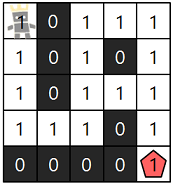
캐릭터가 적 팀의 진영까지 이동하는 가장 빠른 길은 다음 그림과 같습니다.

따라서 총 11칸을 캐릭터가 지나갔으므로 11을 return 하면 됩니다.
입출력 예 #2
문제의 예시와 같으며, 상대 팀 진영에 도달할 방법이 없습니다. 따라서 -1을 return 합니다.
코드
from collections import deque
def solution(maps):
n = len(maps)
m = len(maps[0])
dist = [[0]*m for _ in range(n)]
dr = [-1, 0, 1, 0]
dc = [0, 1, 0, -1]
Q = deque()
Q.append([0, 0])
maps[0][0] = 1
# 시작 좌표도 포함하므로 L = 1
L = 1
while Q:
length = len(Q)
for _ in range(length):
r, c = Q.popleft()
for i in range(4):
nr = r + dr[i]
nc = c + dc[i]
if 0 <= nr and nr < n and 0 <= nc and nc < m and maps[nr][nc] == 1:
Q.append([nr, nc])
maps[nr][nc] = 0
dist[nr][nc] = L + 1
L += 1
if dist[n-1][m-1] == 0:
return -1
else:
return dist[n-1][m-1]풀이
이 문제는 이전에 풀었던 BFS - 미로의 최단거리 통로 문제와 매우 흡사하다.
먼저 maps의 크기와 같은 해당 좌표까지의 최소 거리를 표시할 2차원 배열 dist를 만든다.
이 2차원 배열을 0으로 다 초기화한 후 만약 탐색이 끝났을 때도 탈출 좌표의 값이 0이면 탈출하지 못한 것을 의미하므로, -1을 리턴해준다.
또한, 벽이 있는 자리(0)는 중복으로 이동하지 않도록 벽이 없는 자리(1)으로 바꿔준다.
또, dr, dc 방향 배열을 만들어 움직일때마다 격자판을 나가지 않는지, 이미 지나온 길이 아니면서, 벽이 없는 자리인지를 확인해 자식 노드를 계속 생성해나간다.
따라서 갈 수 있는 길을 모두 탐색한 후 탈출 좌표의 최소 거리를 나타내는 dist[n-1][m-1]의 값이 0이면 탈출하지 못 한 것이므로 return -1을 하고 탈출에 성공했다면 return dist[n-1][m-1]을 해 탈출 좌표까지의 최소 거리를 출력해준다.
