fractal - 그래픽 라이브러리 사용해보기

YSHAM·2022년 12월 30일

42서울 c언어 mlx zoom알고리즘

42Seoul

목록 보기

6/18

들어가기에 앞서

그래픽 라이브러리인 mlx에 대해 충분히 공부 : 팔만코딩경 mlx
내가 그리려는 fractal에 대해 수식 파악
mlx를 실행시키는 Makefile과 gcc컴파일 방식 파악

🖥️ Mandatory

fractal이미지인 Mandelbrot과 Julia를 구현하는게 목표입니다.

우선 Makefile이나 컴파일 방식에 대해 파악하셔야 합니다.

컴파일

gcc -I ./minilibx_mms_20210621 -c test.c

동적 라이브러리는 mms 디렉토리에 위치해 있고, mms 디렉토리에는 mlx.h라는 파일w이 존재하는 것을 볼 수 있습니다. 따라서 gcc -c로 컴파일 할 때, mms 디렉토리를 -I 옵션으로 명시하여 Header의 위치를 잡아주도록 합니다. 아래 그림처럼 test.o라는 목적 파일이 생성된 것을 확인할 수 있습니다.

gcc -L ./minilibx_mms_20210621 -lmlx -framework OpenGL -framework AppKit -o test test.o

생성된 목적 파일을 실행 파일로 만들기 위해, -L 옵션을 통해 라이브러리의 위치를 명시하고 -l 옵션을 통해 사용하려는 라이브러리를 명시하여 컴파일을 수행합니다. 또한 "mlx.h"를 이용하여 컴파일 할 때는 -framework OpenGL -framework AppKit이라는 옵션을 함께 명시해줘야 합니다. 아래 그림처럼 test라는 실행 파일이 정상적으로 생성된 것을 확인할 수 있습니다.

minilibx에서 PWD 후 경로 저장

export DYLD_LIBRARY_PATH=’저장한 경로’

test 파일을 실행해보면 test window가 실행되지 않고 dyld: Library not loaded라는 오류를 볼 수 있습니다. 이는 Mac OS X에서 dylib라는 확장자를 갖는 동적 라이브러리를 이용할 때 경로 설정이 되어 있지 않아서 발생하는 오류입니다. 이를 처리하는 방법은 직접적으로 경로를 수정하는 방법과 명령어를 이용하여 경로를 수정하는 방법으로 2가지가 존재합니다.

직접적으로 경로를 수정하는 방법

이 방법을 이용할 때는 DYLD_LIBRARY_PATH를 설정 해줘야 하는데 확인해보면 아무런 값도 설정되어 있지 않은 것을 확인할 수 있습니다.

동적 라이브러리가 위치한 곳의 절대 경로를 확인한 후 이를 DYLD_LIBRARY_PATH로 등록해줍니다.

만일 기존에 동적 라이브러리를 위한 DYLD_LIBRARY_PATH를 이용 중이라면, 기존 경로에 추가해야하므로 export DYLD_LIBRARY_PATH= $DYLD_LIBRARY_PATH:$ newPath와 같이 명령어를 이용하면 됩니다.

DYLD_LIBRARY_PATH에 대한 설정이 되었다면 test를 다시 실행해보면 test window가 실행되는 것을 확인할 수 있습니다.

Makefile

'-L' option : looks in directory for library files. 라이브러리를 찾을 디렉토리를 지정

'-l' option : links with a library file. 같이 링크할 라이브러리 지정

../mlx에 있는 libmlx.h를 찾아서 같이 링크함
프레임워크 관련필요한 프레임워크랑 같이 컴파일
framework OpenGL -framework AppKit

NAME = fractol

SRCS = fractal.c mandelbrot.c julia.c mlx_utils.c ft_atod.c
REAL_SRCS = $(addprefix mandatory/, $(SRCS))

BO_SRCS = fractal_bonus.c burningship_bonus.c mlx_utils_bonus.c
REAL_BO_SRCS = $(addprefix bonus/, $(BO_SRCS))

OBJS = $(REAL_SRCS:%.c=%.o)

BO_OBJS = $(REAL_BO_SRCS:%.c=%.o)

CFLAGS = -Wall -Wextra -Werror

CLIB = -Lmlx -lmlx -framework OpenGL -framework Appkit

ifdef WITH_BONUS
	OBJ_FILE = $(BO_OBJS)
else
	OBJ_FILE = $(OBJS)
endif

all : $(NAME)

$(NAME): $(OBJ_FILE)
	cc $(CFLAGS) $(CLIB) $(OBJ_FILE) -o $(NAME)

%.o : %.c
	cc $(CFLAGS) -c $< -o $@

clean :
	rm -f $(OBJS) $(BO_OBJS)

fclean :
	make clean
	rm -f $(NAME)

re : 
	make fclean
	make all

bonus:
	@make WITH_BONUS=1 all

.PHONY : all clean fclean re bonus

fractal

프랙탈(Fractal)

일부 작은 조각이 전체와 비슷한 기하학적인 형태로 재귀적이거나 반복적인 작업에 의한 패턴으로 만들어집니다.
아래 위키백과에 설명이 무척이나 잘 되어있으니 한번 읽어보면 큰 도움이 됩니다.

프랙탈 위키백과
망델브로 위키백과
줄리아 위키백과

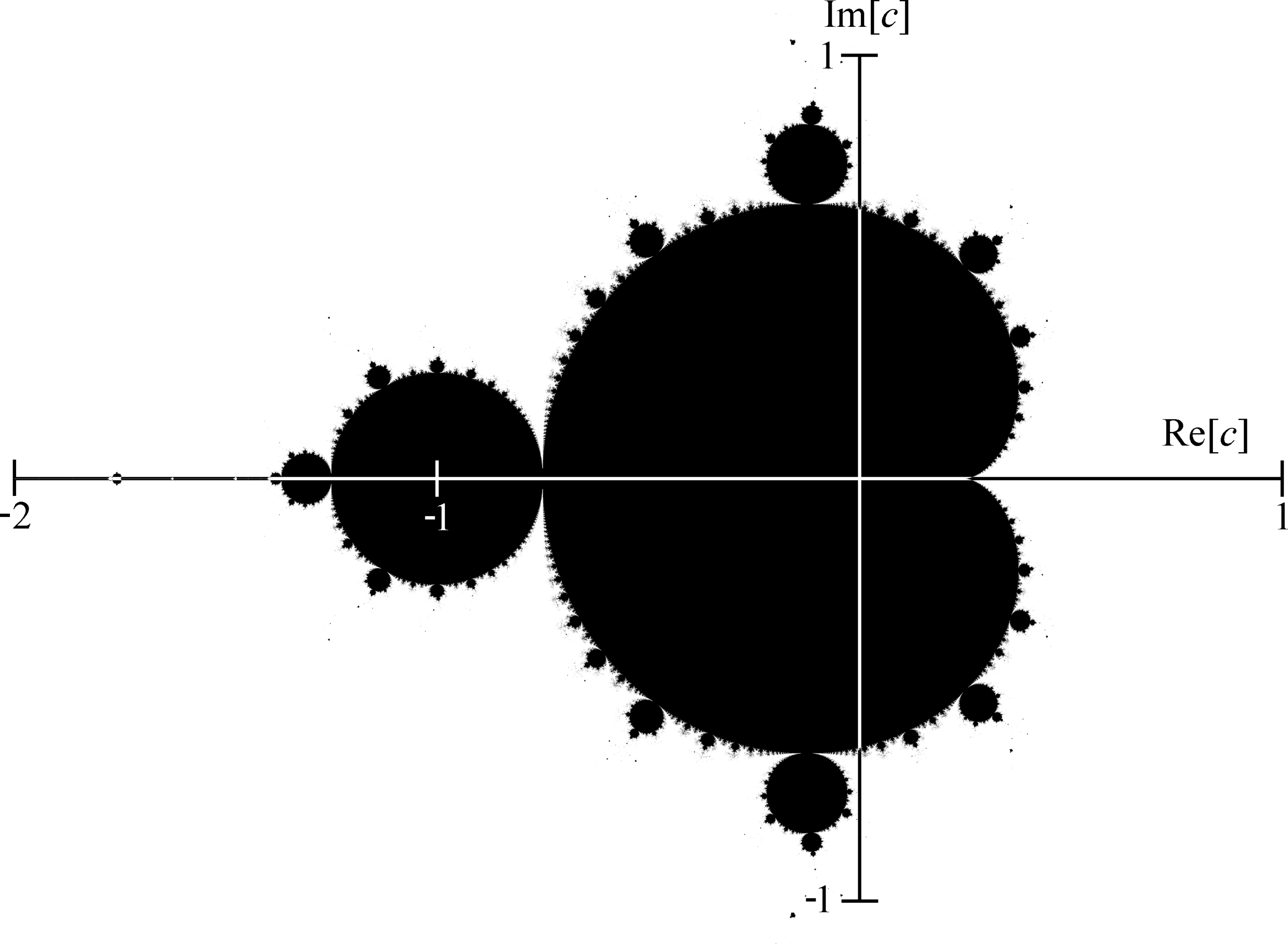
복수평면에서 망델브로 집합은 다음 점화식으로 정의된 수열이 발산하지 않는 성질을 갖도록 하는 복소수 c의 집합으로 정의됩니다.

$Z n+1 =Z n2 +C (Z, C는 복소수)$
$M = \{C: Z_{n+1} = Z_n^2+C, \lim\limits_{n\to\infty}\left\vert Z_n\right\vert<\infty\}$

무한대로는 계산할 수 없기 때문에 $\lim\limits_{n\to\infty}\left\vert Z_n\right\vert<2$ 로 계산합니다.

해당 식을 실수부, 허수부로 나누면
$X_{n+1} = X_n^2-Y_n^2+a$
$Y_{n+1} = 2X_nY_n+b$
입니다.

줄리아 집합은 정해진 C에 대해 점화식을 수렴시키는 Z의 집합
발산, 수렴이 초기값 Z에 의해 결정됩니다.

$Z n+1 =Z n2 +C (Z, C는 복소수)$
$M = \{Z: Z_{n+1} = Z_n^2+C, \lim\limits_{n\to\infty}\left\vert Z_n\right\vert<\infty\}$

해당 식을 실수부, 허수부로 나누면
$X_{n+1} = X_n^2-Y_n^2+a$
$Y_{n+1} = 2X_nY_n+b$
입니다.

정리하자면,
망델브로는 0으로 시작하는 어떠한 복소수 z가 발산하지 않고 수렴하게 하는 복소수 c값들의 집합을 나타내며,
줄리아는 반대로 복소수 z값들의 집합입니다.

기본적인 fractal 정의와 구현하고자하는 Mandelbrot / Julia의 수식과 mlx사용법 및 Makefile 작성법을 숙지하셨으면 코드 작성으로 들어갑니다.

int	main(int argc, char *argv[])
{
	t_comp	first;

	if (argc == 1)
		printlist();
	if (ft_strcmp(argv[1], "Mandelbrot"))
	{
		if (argc != 2)
			printlist();
		makeman();
	}
	else if (ft_strcmp(argv[1], "Julia"))
	{
		if (argc != 4)
			printlist();
		first.real = ft_atod(argv[2]);
		first.imaginary = ft_atod(argv[3]);
		makejul(&first);
	}
	else
		printlist();
	return (0);
}

실행시키면 인자를 받아 해당값이 Mandelbrot인지 Julia인지 파악합니다.
Julia의 경우 c값의 실수부와 허수부도 인자로 받습니다.

int	makeman(void)
{
	t_data	var;

	var.mlx = mlx_init(); // mlx 생성
	var.mlx_win = mlx_new_window(var.mlx, X_LEN, Y_LEN, "Mandelbrot"); // Mandelbrot이란 이름으로 window에 새창을 띄웁니다.
	var.mlx_img = mlx_new_image(var.mlx, X_LEN, Y_LEN); // 새창에 이미지를 덧씌우고
	var.addr = mlx_get_data_addr(var.mlx_img, &var.bits_per_pixel,
			&var.line_length, &var.endian); // mlx의 데이터로 받을 인자들을 넣어주고
	setting(&var); // 좌표평면의 값을 셋팅해줍니다.
	print_mandelbrot(&var); // Mandelbrot 수식과 범위에 따라 집합을 만들어줍니다.
	mlx_mouse_hook(var.mlx_win, man_mouse_hook, &var); // 마우스 클릭을 인식하는 hook함수도 넣고
	mlx_key_hook(var.mlx_win, man_key_hook, &var); // 키보드 값을 인식하는 hook함수와
	mlx_hook(var.mlx_win, 17, 0, x_exit, &var); // 좌측상단 종료버튼을 눌렀을경우 쉘 스크립트도 종료하는 exit함수로 동작시켜줍니다.
	mlx_loop(var.mlx); // 해당 hook함수를 loop시켜 계속 동작시켜줍니다.
	return (0);
}

Mandelbrot을 실행시켰다면 해당 함수로 동작합니다.
해당 함수 내부의 mlx 동작은 주석으로 남겼습니다.

int	mandel_code(double i, double j, t_data *var)
{
	t_comp	z;
	t_comp	c;
	double	temp;
	int		n;

	z.real = 0;
	z.imaginary = 0;
	c.real = var->left + i * (var->xlen) / X_LEN;
	c.imaginary = var->top + j * (var->ylen) / Y_LEN;
	n = 0;
	while ((z.real * z.real) + (z.imaginary * z.imaginary) <= 4 && n < N_MAX)
	{
		temp = 2 * z.real * z.imaginary;
		z.real = (z.real * z.real) - (z.imaginary * z.imaginary) + c.real;
		z.imaginary = temp + c.imaginary;
		n++;
	}
	return (n);
}

앞서 공부했던 fractal 수식들을 코드로 구현합니다.
math.h 헤더에 있는 pow함수로 제곱계산을 해도 되지만 속도가 더 느려저 단순하게 곱하기로 계산했습니다.

int	print_mandelbrot(t_data *var)
{
	double		i;
	double		j;
	int			n;

	mlx_clear_window(var->mlx, var->mlx_win);
	i = 0;
	while (i < X_LEN)
	{
		j = 0;
		while (j < Y_LEN)
		{
			n = mandel_code(i, j, var);
			if (n == N_MAX)
				my_mlx_pixel_put(var, i, j, 0X00000000);
			else
				my_mlx_pixel_put(var, i, j, color(n, var->flag));
			j++;
		}
		i++;
	}
	mlx_put_image_to_window(var->mlx, var->mlx_win, var->mlx_img, 0, 0);
	return (0);
}

이전 수식의 리턴값을 가져와 몇번째에서 발산하는지 파악 후 색상을 다르게 표현하여 이미지의 층을 나타내줍니다.

해당 코드를 실행시켜 망델브로와 줄리아 집합을 완성시키면 됩니다.
줄리아의 경우 마우스클릭도 인자로 받아 커서 위치를 좌표평면으로 변환하여 인자로 받게 만들어 클릭하면 이미지가 바뀝니다.

💻 Bonus

해당 파트에서는 2개의 프랙탈 이미지 외 다른 프랙탈을 하나 더 만들고, 방향키로 이미지 이동 및 커서 위치에 따라 확대와 축소, 다양한 색상변경 옵션을 추가하는 파트입니다.

int	ship_code(double i, double j, t_data *var)
{
	t_comp	z;
	t_comp	c;
	double	temp;
	int		n;

	z.real = 0;
	z.imaginary = 0;
	c.real = var->left + i * (var->xlen) / X_LEN;
	c.imaginary = var->top + j * (var->ylen) / Y_LEN;
	n = 0;
	while ((z.real * z.real) + (z.imaginary * z.imaginary) <= 4 && n < N_MAX)
	{
		temp = fabs(-2 * (z.real) * (z.imaginary));
		z.real = (z.real * z.real) - (z.imaginary * z.imaginary) + c.real;
		z.imaginary = temp + c.imaginary;
		n++;
	}
	return (n);
}

프랙탈 이미지 모습이 배가 불에 타고있는 모습과 유사하여 burning ship이라 불리는 프랙탈을 만들었습니다.

$z_{{n+1}}=(|\operatorname {Re}\left(z_{n}\right)|+i|\operatorname {Im}\left(z_{n}\right)|)^{2}+c,\quad z_{0}=0$

수식은 Mandelbrot과 비슷하나 절댓값 처리를 해줘야 하는 차이가 있습니다.

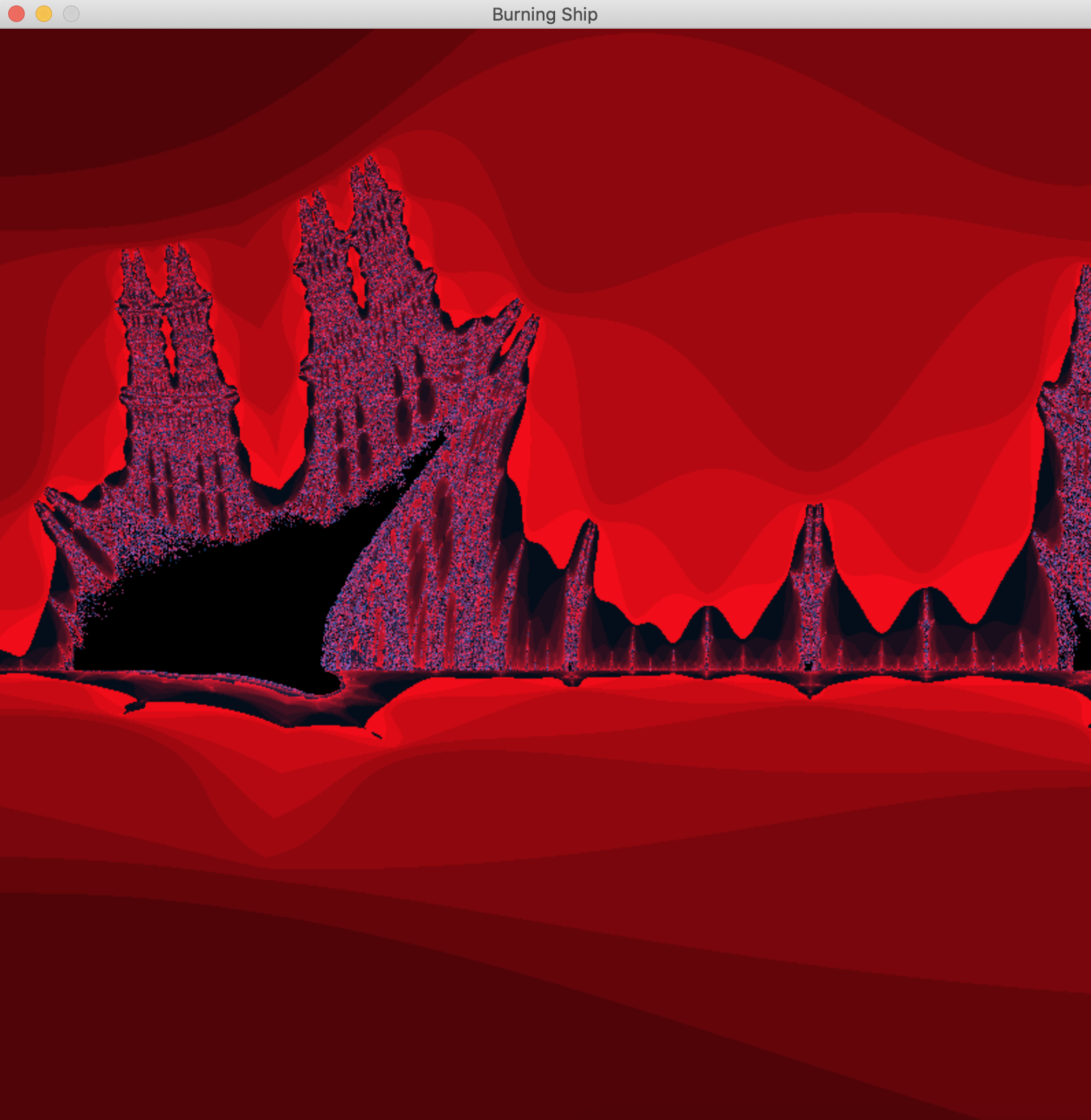
zoom in 과 zoom out은 우리가 자주 사용하는 지도 앱과 같이 마우스 커서를 기준으로 확대/축소가 되어야 합니다.

생각보다 해당 파트를 구현하는데 상당히 오랜 시간이 걸렸습니다.
해당 파트 때문에 작성한 코드도 다 갈아엎고 새로 작성해서 다음부터는 코드를 작성할 때 여러 사항과 요소들을 고려해서 짜야한다는걸 배웠습니다.

색상 변경 옵션은 키보드 키값에 따라 flag를 지정하여 변경하는 방식으로 진행했습니다.

int	color(int n, int flag)
{
	int	color;
	int	ff;

	ff = 256;
	if (flag == 0)
		color = ((n * 20) % ff << 16) + ((n * 20) % ff << 8) + ((n * 20) % ff);
	if (flag == 1)
		color = ((n * 20) % ff << 16) + ((n * 1) % ff << 8) + ((n * 2) % ff);
	if (flag == 2)
		color = ((n * 40) % ff << 16) + ((n * 10) % ff << 8) + ((n * 30) % ff);
	if (flag == 3)
		color = ((n * 10) % ff << 16) + ((n * 50) % ff << 8) + ((n * 20) % ff);
	if (flag == 4)
		color = ((n * 10) % ff << 16) + ((n * 20) % ff << 8) + ((n * 40) % ff);
	return (color);
}

TRGB 형식을 사용하기 위해 비트연산을 활용했습니다.
색상을 표현하기 위한 형식은 0xTTRRGGBB와 같이 초기화해서 사용하며, 각 코드는 다음을 의미합니다.
T : 투명도
R : Red color
G : Green color
B : Blue color
mlx에선 T옵션은 적용되지 않습니다.