스택을 활용한 계산기 구현
구현할 계산기 특징
오늘 공부해본 계산기는 바로 수식을 계산하는 계산기이다
쉽게 말해 일반적으로 숫자의 계산 결과를 출력하는 계산기가 아닌
(3+1) * 4 / (1+2) 이런 수식을 받으면 계산을 하는 계산기를 구현해 볼거다
수식의 표기법
수식의 표현법에는 3개 존재한다
1.중위 표기법
2.전위 표기법
3.후위 표기법
여기서는 1,3번만을 정리해 보겠다
중위 표기법
중위 표기법 이란 우리가 평소에 쓰는 표기법이다
예) 3+5 ,(4+2)/2
이런식으로 피연산자 사이에 연산자가 존재하는 형태이다
후위 표기법
후위 표기법은 연산자가 피연사자 뒤에 들어가는 표기법이다
예)3+5(중위) => 35+(후위) , (4+2)/2 => 42+2/(후위)
그러면 이제 중위 표기법으로 작성된 수식을 후위 표기법으로 바꾸는 방법을 알아보자
중위 표기법 => 후위 표기법 : 소괄호 고려하지 않음
먼저 소괄호가 없는 수식을 계산하는 순서를 알아보자
1.중위 표기법의 수식을 후위 표기법으로 바꾼다
2.후위 표기법으로 변경한 수식을 계산하여 결과를 출력한다
이제 천천히 시작해 보자
5+4/3를 후위 표기법 으로 변환해 보자
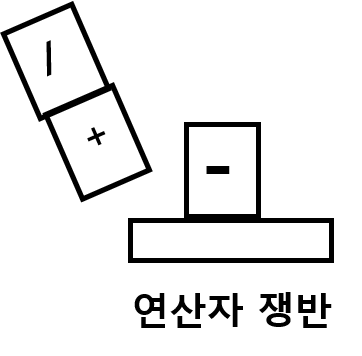
연산자와 피연사자를 각각 1개의 블록으로 생각하고 연산자를 담는 그릇을 상상해보자

변환의 1번째 규칙
피연산자는 그냥 후위표식에 넣는다
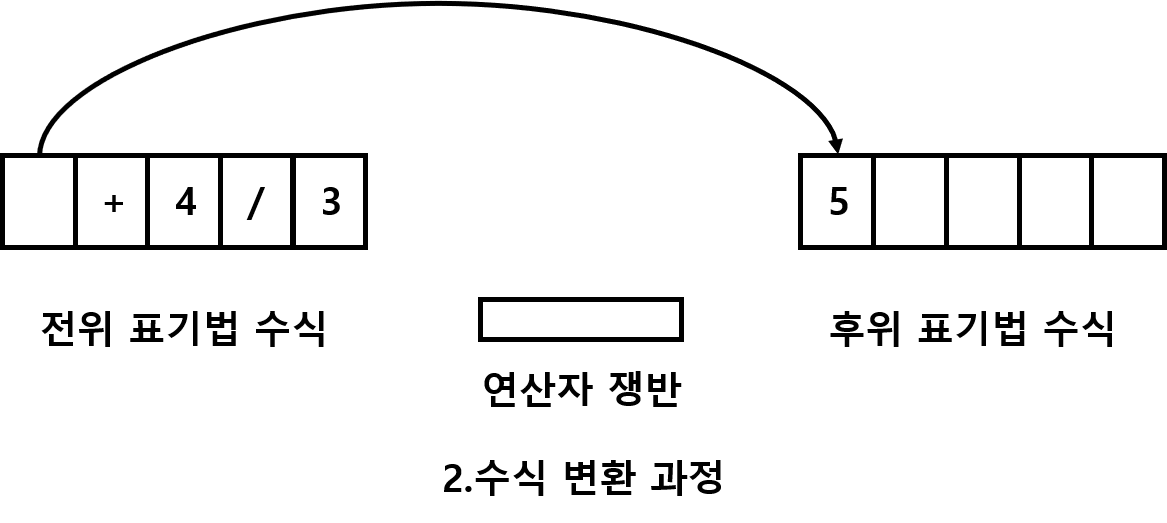
변환의 2번째 규칙
연산자는 일단 쟁반으로 간다
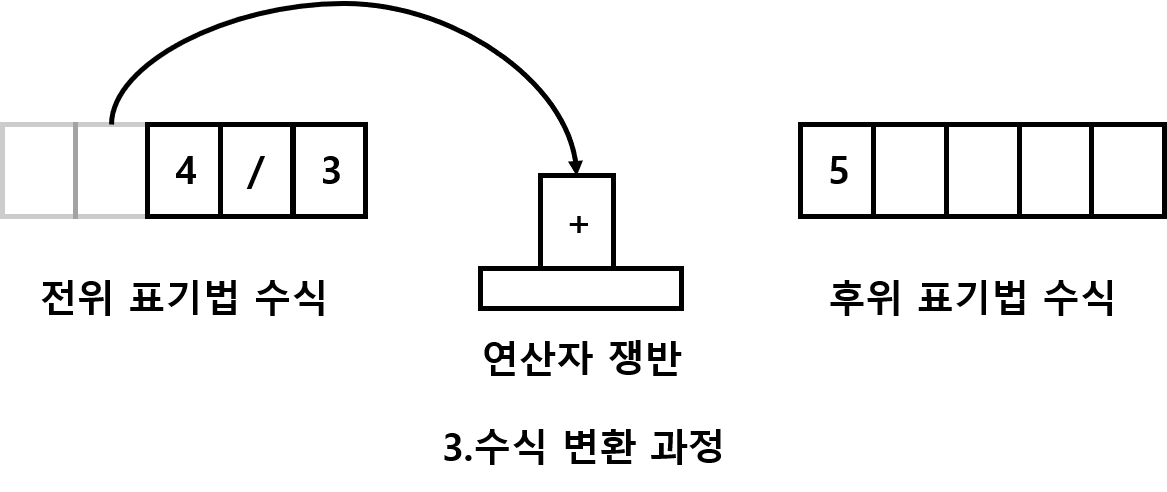
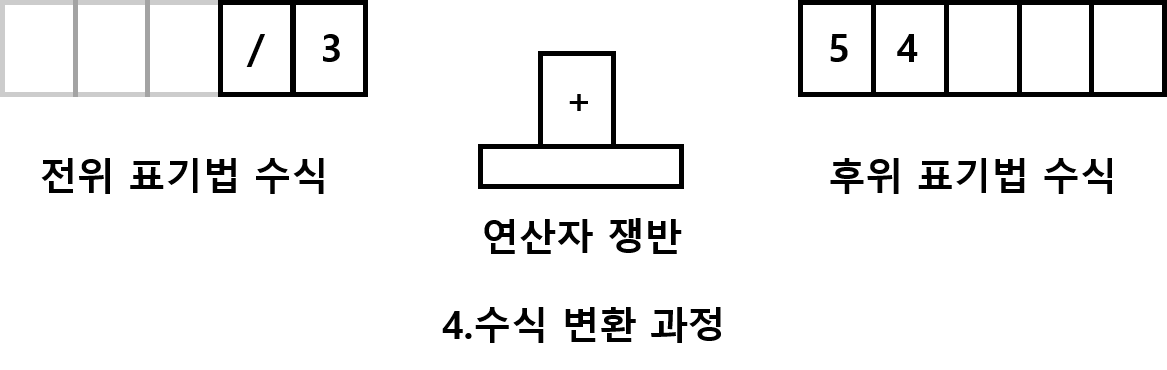
변환의 3번쨰 규칙
1.쟁반에 위치한 연산자가 들어가야할 연산자 보다 우선순위가 높다
=> 쟁반에 위차한 연산자를 꺼내서 변환된 수식이 위치할 자리로 옮긴다
2.쟁반에 위치한 연산자의 우선순위가 낮다
=>쟁반에 위치한 연산자 위에 연산자를 쌓는다
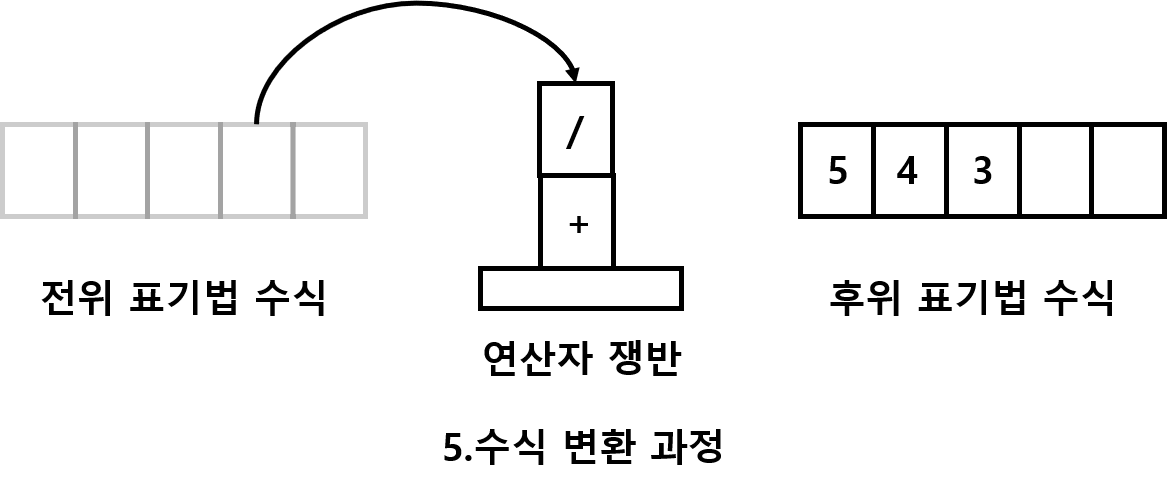
변환의 4번쨰 규칙
피연사자를 전부 옮긴후 쟁반에 남아있는 연산자를 위에서 부터 순서대로 넣는다
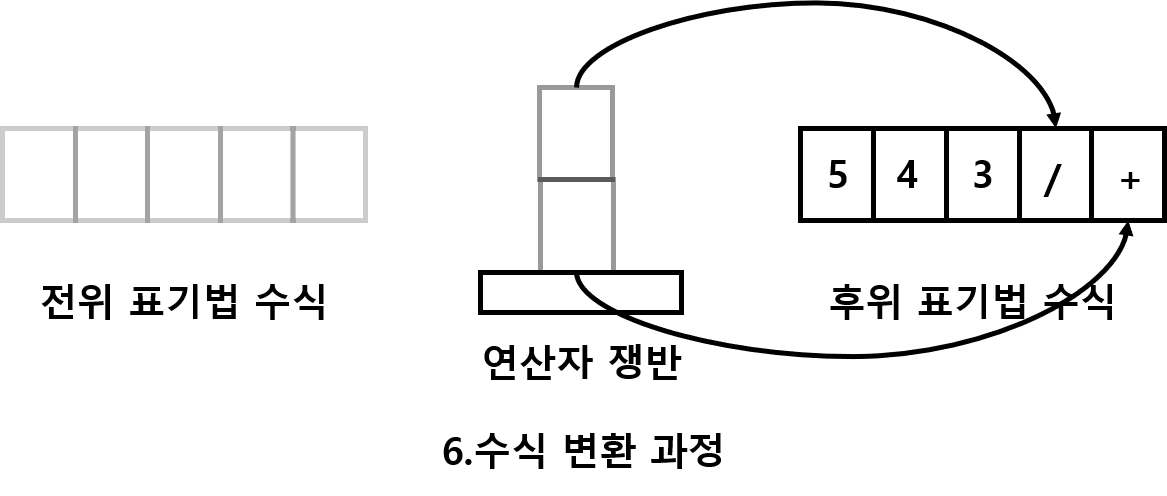
대략적인 변환 방식을 알아봤는데 특수한 상황 몇가지를 살펴보자
1.접시에 놓인 연사자와 올려질 연산자가 우선순위가 같은 경우
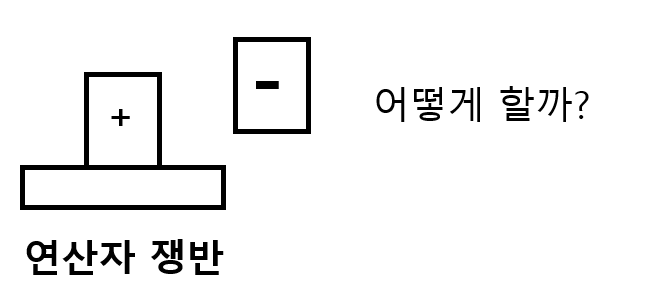
이런경우에는 간단하다 먼저 접시에 놓인 연산자를 빼주고서 접시에 올리면 해결된다
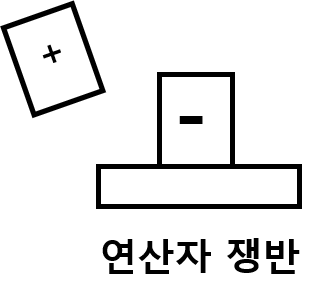
2.그림으로 상황을 보자
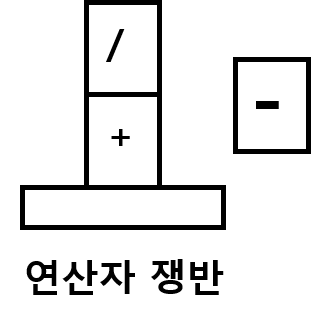
접시에 쌓인 연산자를 모두 빼내고 쌓으면 된다
중위 표기법 => 후위 표기법 : 소괄호 고려하기
수식 (1+2 * 3) / 4 를 후위 표기법으로 바꿔보자
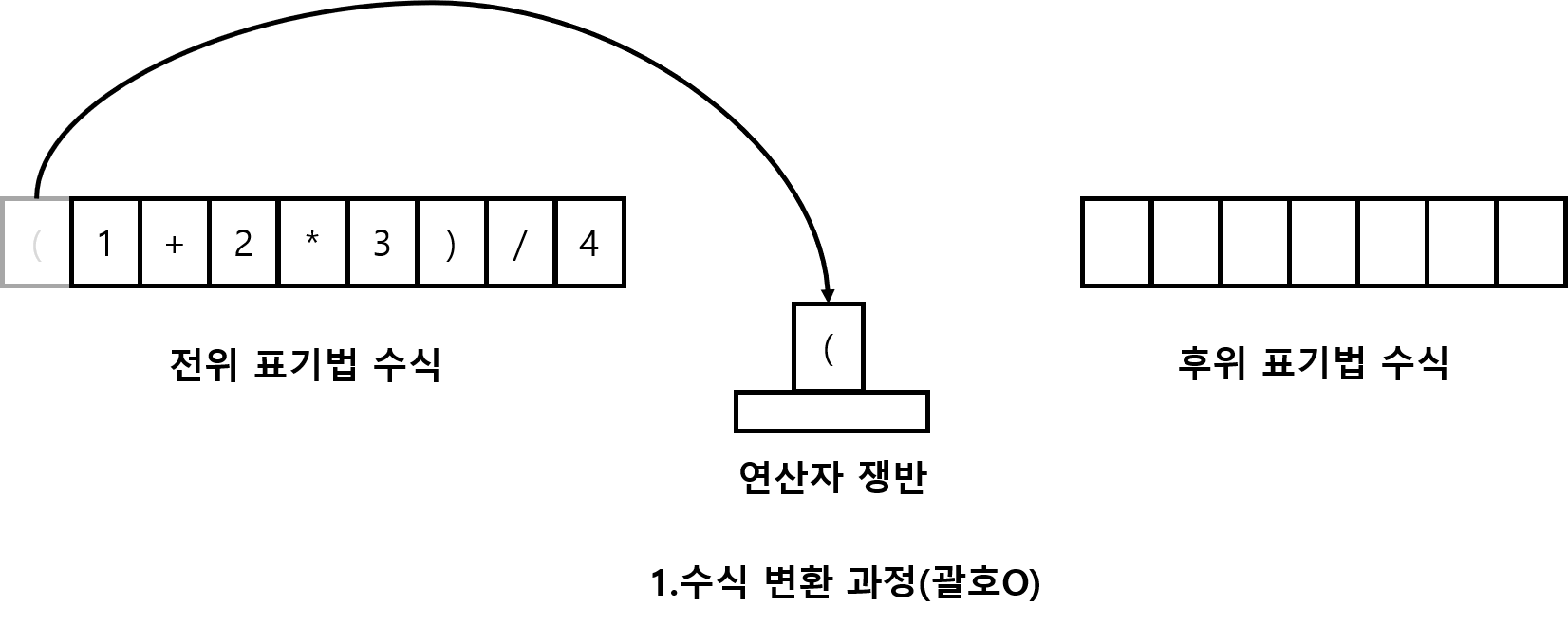
괄호도 일반적으로 1칸을 차지한다고생각하고 연산자 취급을 해보자

(연산자가 놓이게되면 )연산자가 나올때 까지 ( 괄호 안 연사자 ) 들은 모두 쟁반위에서 존재해야한다
이것은 (을 제일 낮은 우선순위의 연산자로 취급한다느 것이다
나머지는 이제 위에서 했던것 처럼 옮기면 된다
이러한 방식을 코드를 통해서 어떻게 구현했는지 정리해보자
표기법 변환 프로그램 구현
중위 표기법에서 후위 표기법으로 변환하는 프로그램을 구현하는데 있어 필요한 코드들을 분석해보자
int GetOpPrec(char op)
{
switch(op)
{
case '*':
case '/':
return 5;
case '+':
case '-':
return 3;
case '(':
return 1;
}
return -1; // 등록되지 않은 연산자
}연산자들의 우선순위를 표시하기 위해서 사용한다
우선순위가 높을수록 반환값이 크다는 사실을 확인할수있다
int WhoPrecOp(char op1, char op2)
{
int op1Prec = GetOpPrec(op1);
int op2Prec = GetOpPrec(op2);
if(op1Prec > op2Prec)
return 1;
else if(op1Prec < op2Prec)
return -1;
else
return 0;
}인자로 전달한 연산자들의 우선순위를 비교해서 반환값을 반환하는 함수
void ConvToRPNExp(char exp[])
{
Stack stack;
int expLen = strlen(exp);
char * convExp = (char*)malloc(expLen+1);
int i, idx=0;
char tok, popOp;
memset(convExp, 0, sizeof(char)*expLen+1);
StackInit(&stack);
for(i=0; i<expLen; i++)
{
tok = exp[i];
if(isdigit(tok))
{
convExp[idx++] = tok;
}
else
{
switch(tok)
{
case '(':
SPush(&stack, tok);
break;
case ')':
while(1)
{
popOp = SPop(&stack);
if(popOp == '(')
break;
convExp[idx++] = popOp;
}
break;
case '+': case '-':
case '*': case '/':
while(!SIsEmpty(&stack) &&
WhoPrecOp(SPeek(&stack), tok) >= 0)
convExp[idx++] = SPop(&stack);
SPush(&stack, tok);
break;
}
}
}
while(!SIsEmpty(&stack))
convExp[idx++] = SPop(&stack);
strcpy(exp, convExp);
free(convExp);
}위 코드를 정말 하나하나 천천히 분석해 보자
Stack stack;
int expLen = strlen(exp);
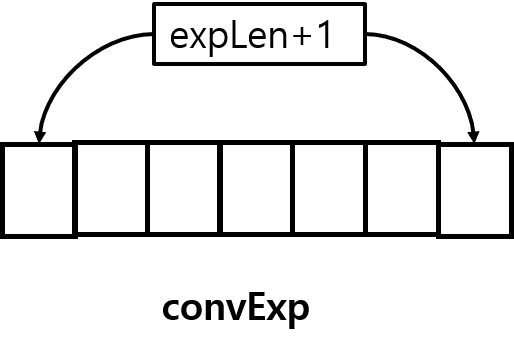
char * convExp = (char*)malloc(expLen+1); 후위식 변환함수의 인자로 준 중위 표기법 수식의 길이를 expLen이 가지면서
후위 표기로 변환된 수식을 저장할 공간을 할당한다
int i, idx=0;
char tok, popOp;
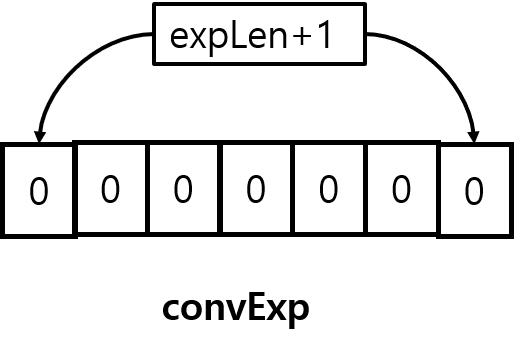
memset(convExp, 0, sizeof(char)*expLen+1);
StackInit(&stack);
for(i=0; i<expLen; i++)
{
tok = exp[i];
if(isdigit(tok))
{
convExp[idx++] = tok;
} memset 함수를 통해 후위 표기 수식을 저장할 공간에 0을 채워넣는다
tok = exp[i]; 인자로 넘긴 중위 표기 수식의 각각의 char 값을 저장한다
if(isdigit(tok))
{
convExp[idx++] = tok;
}tok 값이 숫자(피연사자)라면 바로 후위 표기식을 담을 공간에 넣어줘라
else
{
switch(tok)
{
case '(':
SPush(&stack, tok);
break;
case ')':
while(1)
{
popOp = SPop(&stack);
if(popOp == '(')
break;
convExp[idx++] = popOp;
}
break;
case '+': case '-':
case '*': case '/':
while(!SIsEmpty(&stack) &&
WhoPrecOp(SPeek(&stack), tok) >= 0)
convExp[idx++] = SPop(&stack);
SPush(&stack, tok);
break;
}
}switch문의 각각의 상황에 따라서 어떤식으로 진행되는지 살펴보자
1."("경우
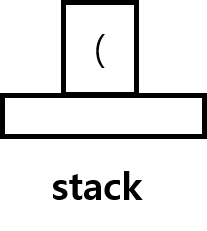
스택(접시)위에 쌓으면 된다
2")"경우
"("를 만날때 까지 스택위에 쌓여있는 연산자들을 전부 후위 수식 으로 옮겨라
3"+,-,*,/"경우
스택에 연산자가 존재 그리고 스택 맨위에 있는 연산자가 넣을 연산자 보다 우선순위가 같거나 높다면
맨위에 있는 연산자를 후위 수식 그릇에 넣어라
그게 아니라면 인자로 받는 tok를 스택에 쌓아라
그러면 이제 (1+2/3)+2를 후위 표기로 변환하는 과정을 위 코드의 흐름대로 따라가보자
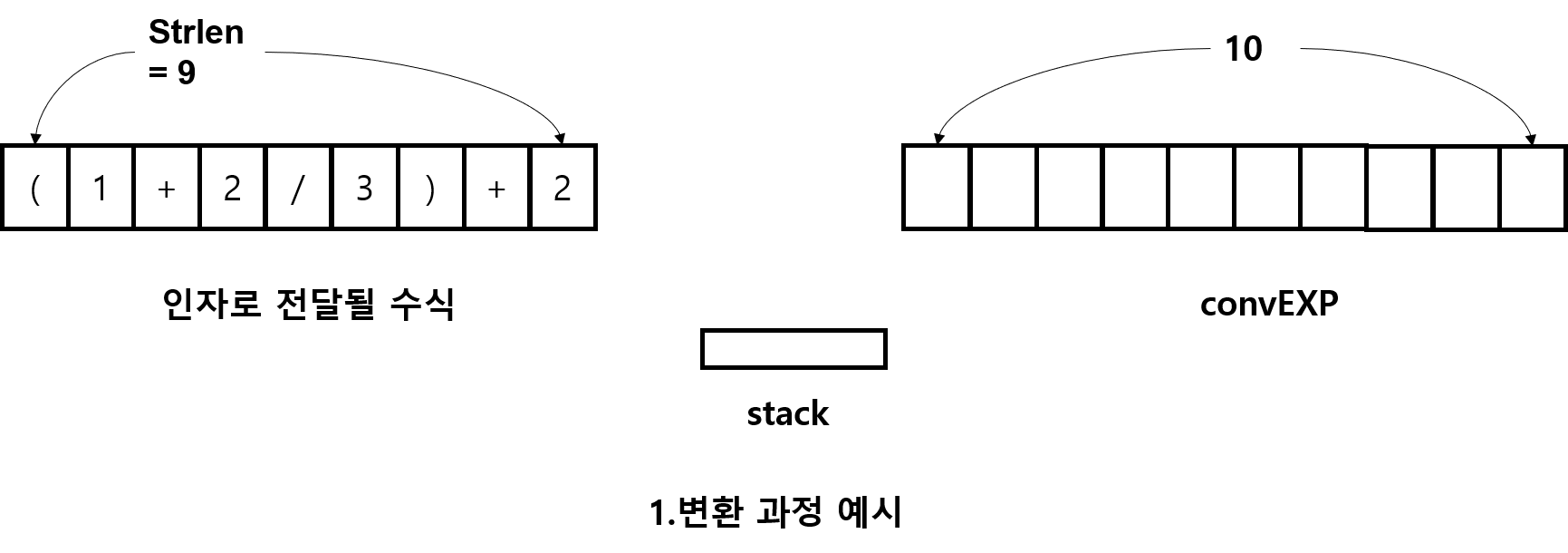
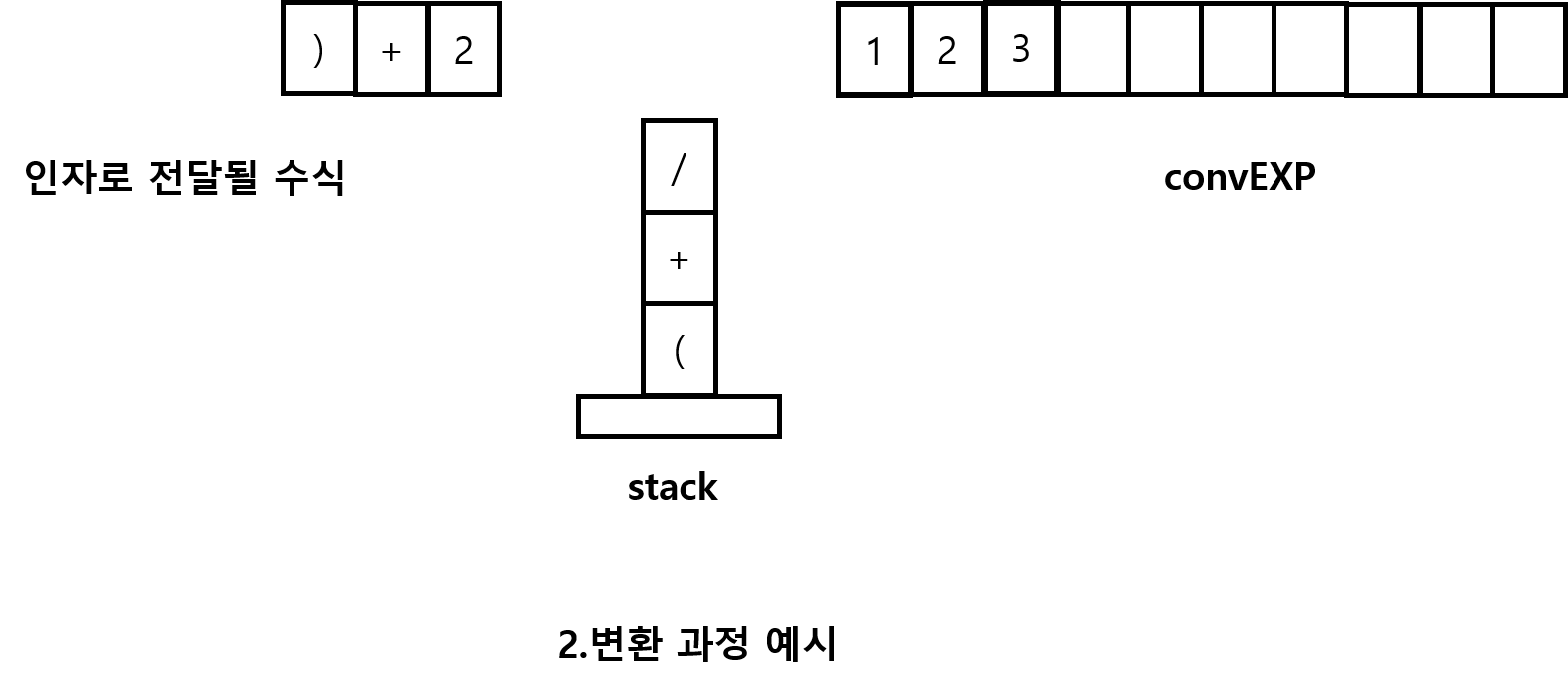
")"나오기 전까지는 우리가 미리 공부한 약속대로 후위 표기식에 숫자와 스택에 연산자를 넣어줬다
")"을 어떻게 처리하는 흐름을 살펴보자
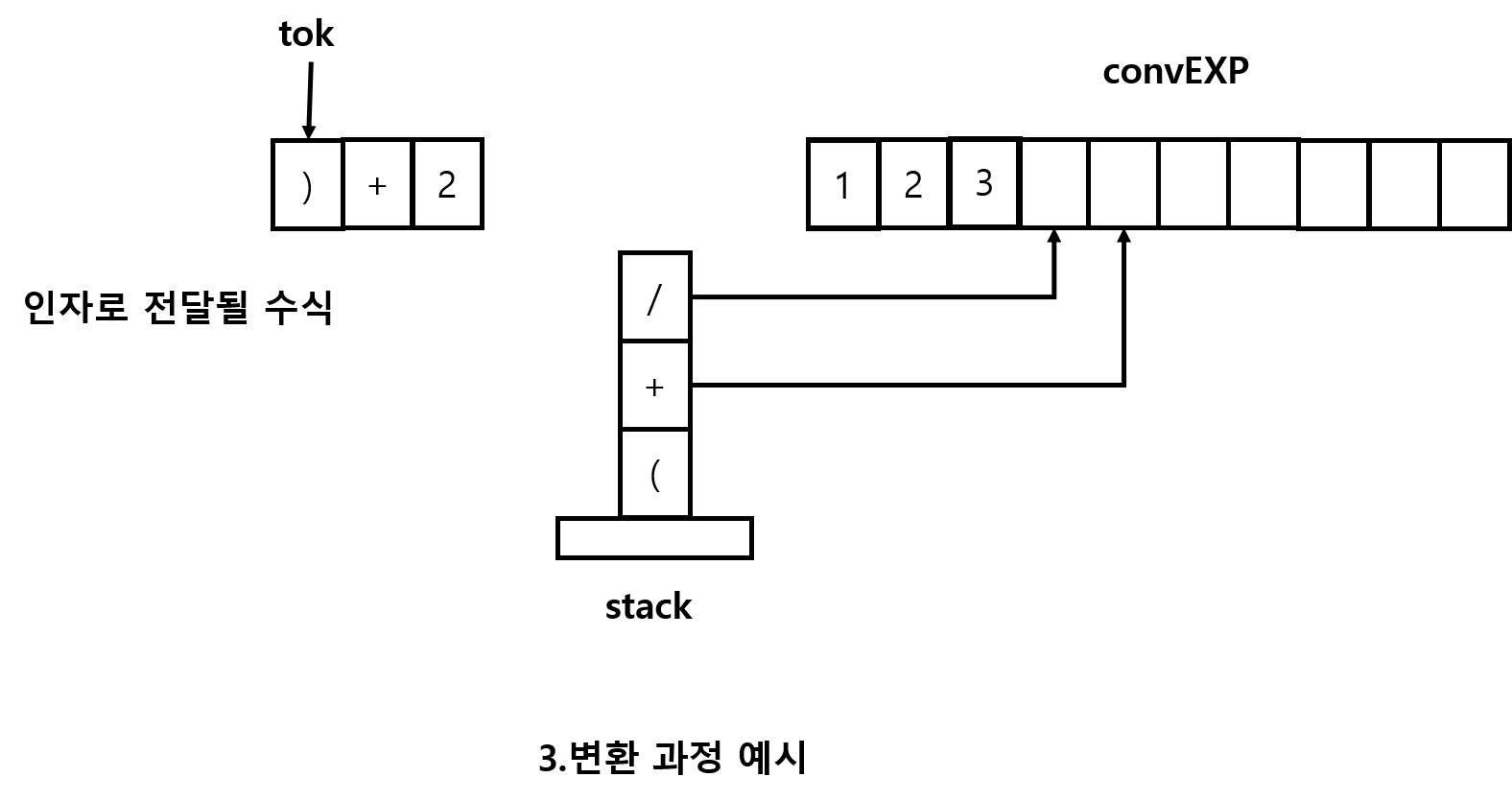
switch(tok)
{
case '(':
SPush(&stack, tok);
break;
case ')':
while(1)
{
popOp = SPop(&stack);
if(popOp == '(')
break;
convExp[idx++] = popOp;
}
break;tok = ) 이므로 )일경우 무한 반목문으로 가서 "(" 나올때 까지 스택위에 연산자들을 convEXP에 넣어주면 된다
이렇게 하면 괄호를 포함한 중위 표기식을 후위 표기식으로 바꿀수있다
후위 표기법 계산 프로그램 구현
후위 표기법 계산은 개인적으로 변환과정보다 훨씬 간단했다
3가지 규칙만 지켜주면 정말로 간단하다
1.피연사자는 무조건 스택으로
2.연산자를 만나면 스택에서 2개 꺼내서 계산한다
3.계산결과를 다시 스택에 넣는다
괄호이런거 신경쓸게 하나없다
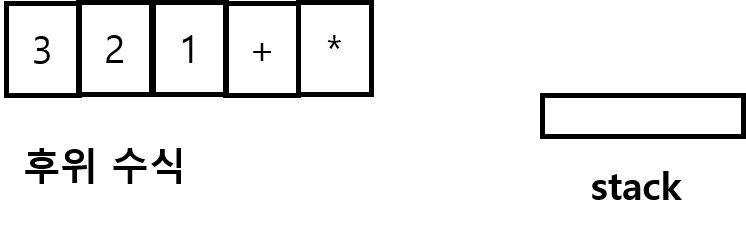
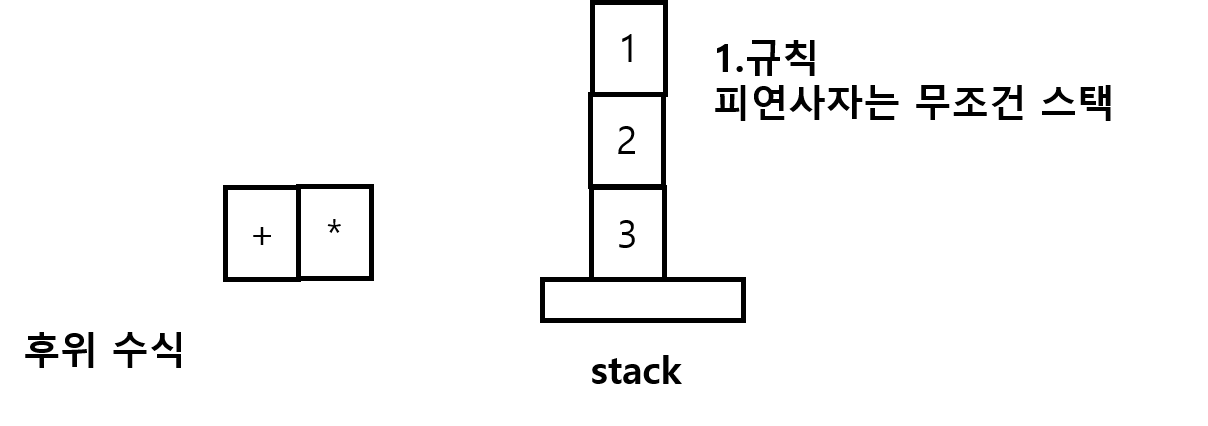

그다음은 생략하겠다
코드를 통해 계산 구현하기
int EvalRPNExp(char exp[])
{
Stack stack;
int expLen = strlen(exp);
int i;
char tok, op1, op2;
StackInit(&stack);
for(i=0; i<expLen; i++)
{
tok = exp[i];
if(isdigit(tok))
{
SPush(&stack, tok - '0'); // 숫자로 변환하여 PUSH!
}
else
{
op2 = SPop(&stack); // 먼저 꺼낸 값이 두 번째 피연산자!
op1 = SPop(&stack);
switch(tok)
{
case '+':
SPush(&stack, op1+op2);
break;
case '-':
SPush(&stack, op1-op2);
break;
case '*':
SPush(&stack, op1*op2);
break;
case '/':
SPush(&stack, op1/op2);
break;
}
}
}
return SPop(&stack);
}간단해서 설명은 생략하겠다
SPush(&stack, tok - '0');
아스키코드 에서 숫자로 변환하는 과정이다
이렇게 해서 공부해본 계산기 프로그램을 정리해 보았다
