[백준] 1948번: 임계경로 with Python

BOJ 1948

• Topological Sorting

문제

---

월드 나라는 모든 도로가 일방통행인 도로이고, 싸이클이 없다. 그런데 어떤 무수히 많은 사람들이 월드 나라의 지도를 그리기 위해서, 어떤 시작 도시로부터 도착 도시까지 출발을 하여 가능한 모든 경로를 탐색한다고 한다.

이 지도를 그리는 사람들은 사이가 너무 좋아서 지도를 그리는 일을 다 마치고 도착 도시에서 모두 다 만나기로 하였다. 그렇다고 하였을 때 이들이 만나는 시간은 출발 도시로부터 출발한 후 최소 몇 시간 후에 만날 수 있는가? 즉, 마지막에 도착하는 사람까지 도착을 하는 시간을 의미한다.

어떤 사람은 이 시간에 만나기 위하여 1분도 쉬지 않고 달려야 한다. 이런 사람들이 지나는 도로의 수를 카운트 하여라.

출발 도시는 들어오는 도로가 0개이고, 도착 도시는 나가는 도로가 0개이다.

풀이과정

---

이 문제의 해결하기 위해서 세 가지를 고려해야 했다.

첫 번째는 위상 정렬 알고리즘이다. 시작 도시부터 도착 도시까지 가는 여러 가지 경로에 대해 탐색을 진행해야하므로 필요하다. 위상정렬을 통해 마지막에 도착하는 사람이 도착하는데 걸리는 시간을 알 수 있다.

두 번째는 경로 추적이다. 단순하게 가장 오래 걸리는 경로를 지나온 사람 1명이 지나간 경로를 계산하면 문제의 정답을 맞출 수 없었다. 이건 스스로 해결하지 못했다. 질문 게시판에 올라온 반례를 통해 알게 되었다.

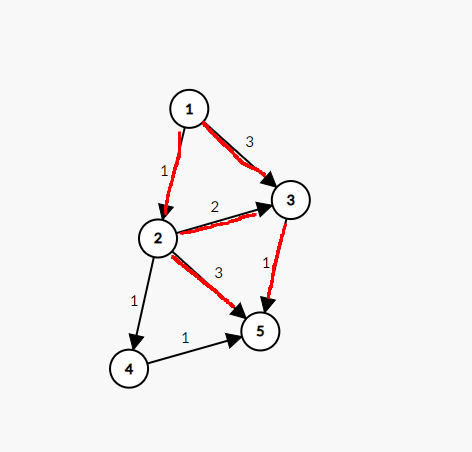
위 그림은 질문 게시판에 baby_ohgu 님께서 올리신 그림이다. 출발 도시가 1, 도착 도시가 5라고 할 때 마지막으로 도착하는 사람이 도착하는데까지 걸리는 시간은 4이다. 여기서 문제가 발생한다. 1->2->5, 1->2->3->5, 1->3->5 모두 4의 시간이 걸린다. 이 문제를 해결하려면 위 경로를 추적해야하는데 간선을 중복해서 계산하면 안된다.

해결 방법은 간단했다. 직전에 지나온 경로를 추적하고, 걸리는 시간에 변화가 생길 때 그 값을 갱신해주면 된다.

        if time[i[1]] < time[now] + i[0]:
            time[i[1]] = time[now] + i[0]
            # 달려야 하는 도로의 수 갱신
            cnt[i[1]] = [now]
        elif time[i[1]] == time[now] + i[0]:
            cnt[i[1]].append(now)

첫 번째 if문 같은 경우에는 i[1]까지 걸리는 시간이 더 오래 걸리는 경로가 나타났을 때이다. i[1]에 도착하기 직전에 거쳐온 노드를 기록한 cnt[i[1]]에 저장된 리스트를 비우고 현재 위치 now를 저장한다. 두 번째 if문은 i[1]까지 걸리는 시간이 같을 경우이다. 이는 도착지까지 같은 시간이 걸리면서 가는 경로가 여러 개 있을 때로 1->2->5, 1->2->3->5 와 같은 경우를 해결하기 위함이다. 이 때는 cnt[i[1]] 리스트에 현재 위치 now를 추가하면 된다.

첫 번째와 두 번째 문제는 해결하니 나의 코드는 히든 케이스도 맞출 수 있었다. 하지만 시간 초과와 메모리 초과가 발생했다. edge의 개수를 세는 과정에서 발생한 문제였다.

q = deque([dst])
route = set()
while q:
    now = q.popleft()
    for x in cnt[now]:
        if (now, x) not in route:
            route.add((now, x))
            q.append(x)

위 코드와 같이 BFS로 지나온 경로들을 역추적 하되, 이미 지나온 경로에 대해서는 큐에 넣지 않아서 시간 초과 문제를 해결할 수 있었다.

코드

---

import sys
from collections import deque

input = sys.stdin.readline

N = int(input())    # N: 도시의 개수
M = int(input())    # M: 도로의 개수

time = [0] * (N+1)
in_degree = [0] * (N+1)
graph = [[] for _ in range(N+1)]
bgraph = [[] for _ in range(N+1)]    # backward of graph
cnt = [[] for _ in range(N+1)]

for _ in range(M):
    # a: 출발 도시, b: 도착 도시, c: 걸리는 시간
    a, b, c = map(int, input().split())
    graph[a].append((c, b))
    bgraph[b].append(a)
    in_degree[b] += 1

src, dst = map(int, input().split())

q = deque([])
# 도시, 지나온 경로 개수
q.append(src)

while q:
    # now: 도시, c: 지나온 경로의 개수
    now = q.popleft()
    # i[0]: 비용, i[1]: 도시
    for i in graph[now]:
        in_degree[i[1]] -= 1
        # 비용이 갱신 될 때
        if time[i[1]] < time[now] + i[0]:
            time[i[1]] = time[now] + i[0]
            # 달려야 하는 도로의 수 갱신
            cnt[i[1]] = [now]
        elif time[i[1]] == time[now] + i[0]:
            cnt[i[1]].append(now)

        # 선행 도로를 모두 지나갔을 때
        if in_degree[i[1]] == 0:
            q.append(i[1])

q = deque([dst])
route = set()
while q:
    now = q.popleft()
    for x in cnt[now]:
        if (now, x) not in route:
            route.add((now, x))
            q.append(x)

print(time[dst])
print(len(route))